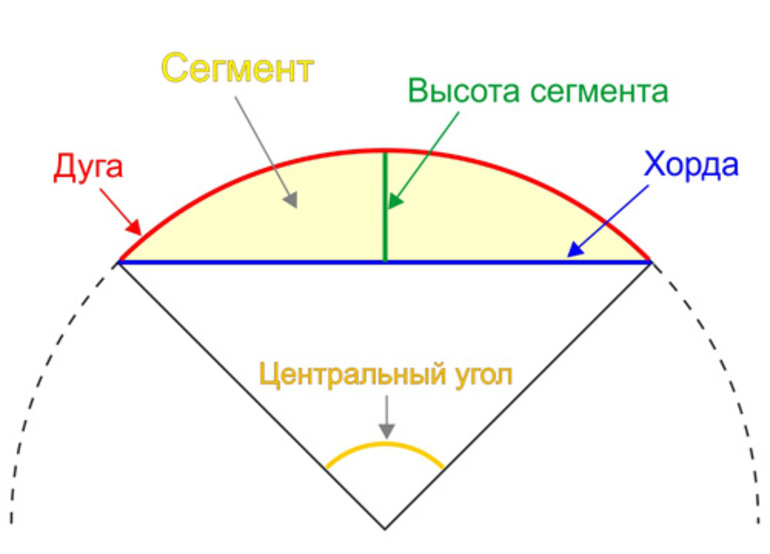
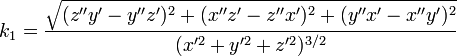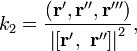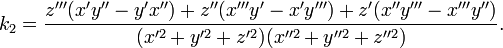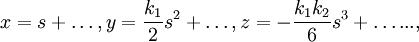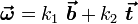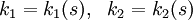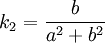- Определение длины дуги
- Формула расчёта длинны дуги
- Пример расчёта длинны дуги
- Длина дуги окружности — формула, обозначение, примеры расчета
- Необходимость расчётов
- Градусная мера
- Применение хорды и высоты
- Практика с задачами
- Усложнение формулы
- Длина дуги
- Содержание
- Способы задания кривой
- Плоские кривые
- Соприкосновение
- Касательная
- Соприкасающаяся плоскость и нормали
- Соприкасающаяся окружность
- Длина дуги кривой
- Параметризация
- Кривизна
- Кручение
- Формулы Френе
- Кинематическое истолкование
- Натуральные уравнения кривой
- Пример
- См. также
- Литература
- Полезное
- Смотреть что такое «Длина дуги» в других словарях:
Определение длины дуги
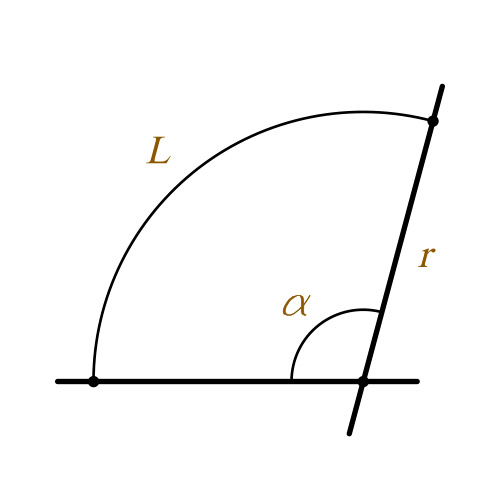
Часть фигуры, которая образует окружность, точки которой равноудалены, называется дугой. Если из точки центра окружности, провести лучи в точки, совпадающие с концами дуги, будет образован её центральный угол.
Определение длины дуги
Формула расчёта длинны дуги
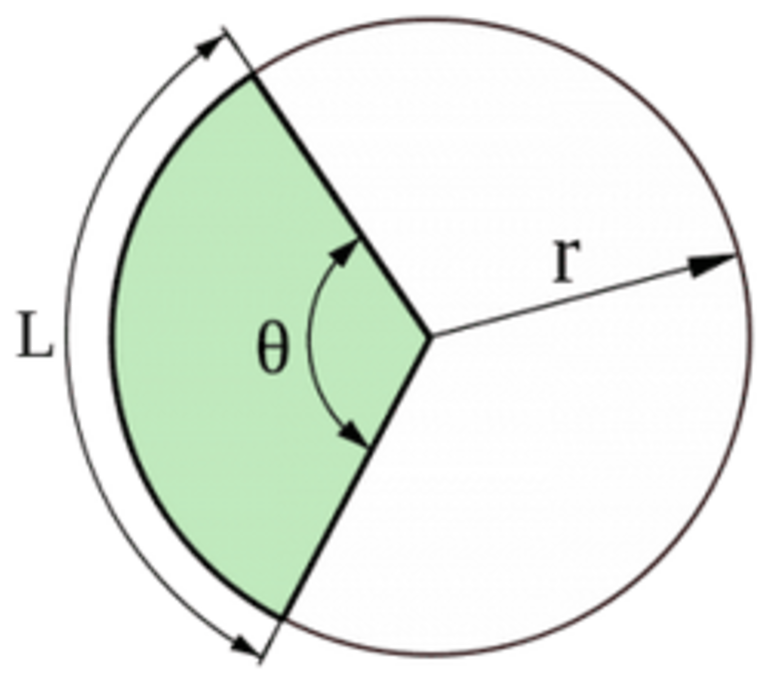
Расчет длины дуги производится по следующей формуле:
r – радиус окружности
Пример расчёта длинны дуги
Нужно определить длину дуги окружности радиусом 10 сантиметров при центральном угле, равном 85° .
где L – искомая длина дуги, π = 3,14 , r – радиус окружности, α – центральный угол.
Длина дуги окружности равна 14,82 сантиметра.
В элементарной геометрии под дугой понимается подмножество окружности, расположенной между двумя расположенными на ней точками. На практике решать задачи по определению ее длины инженерам и архитекторам приходится достаточно часто, поскольку этот геометрический элемент широко распространен в самых разнообразных конструкциях.
Пожалуй, первым, перед кем встала эта задача, были древние зодчие, которым так или иначе приходилось определять этот параметр для сооружения сводов, широко используемых для перекрытия промежутков между опорами в круглых, многоугольных или эллиптических зданиях. Если внимательно присмотреться к дошедшим до наших дней шедеврам древнегреческого, древнеримского и особенно арабского зодчества, то можно заметить, что в их конструкциях дуги и своды встречаются чрезвычайно часто. Творения современных архитекторов ими не так богаты, но эти геометрические элементы наличествуют, конечно же, и в них.
Длину различных дуг необходимо рассчитывать при сооружении автомобильных и железных дорог, а также автодромов, причем во многих случаях от правильности и точности вычислений во многом зависит безопасность движения. Дело в том, что многие повороты магистралей с точки зрения геометрии представляют собой именно дуги, и по движению по ним на транспорт воздействуют различные физические силы. Параметры их результирующей во многом определяются длиной дуги, а также ее центральным углом и радиусом.
Конструкторам машин и механизмов приходится вычислить длины различных дуг для правильной и точной компоновки составных частей различных агрегатов. В данном случае ошибки в расчетах чреваты тем, что важные и ответственные детали будут неправильно взаимодействовать друг с другом и механизм просто не сможет функционировать так, как планируют его создатели. В качестве примеров конструкций, изобилующих такими геометрическими элементами, как дуги, можно привести двигатели внутреннего сгорания, коробки переключения передач, дерево- и металлообрабатывающее оборудование, кузовные элементы легковых и грузовых автомобилей и т.д.
Дуги достаточно широко встречаются в медицине, в частности, в стоматологии. Например, они используются для исправления неправильного прикуса. Корректирующие элементы, называемые брекетами (или брекет-системами) и имеющие соответствующую форму, изготавливаются из специальных сплавов, и устанавливаются таким образом, чтобы изменить положение зубов. Само собой разумеется, что для того, чтобы лечение проходило успешно, эти дуги должны быть очень точно рассчитаны. Кроме того, дуги очень широко используются в травматологии, и, пожалуй, самым ярким примером тому является знаменитый аппарат Илизарова, изобретенный российским врачом в 1951 году и чрезвычайно успешно используемый по сей день. Неотъемлемыми его частями являются металлические дуги, снабженные отверстиями, через которые продеваются специальные спицы, и являющиеся основными опорам всей конструкции.
Источник
Длина дуги окружности — формула, обозначение, примеры расчета
Необходимость расчётов
Геометрическими формулами, связанными с подсчетом площади сектора, объема сегмента и периметра полукруга, следует виртуозно владеть людям, связавшим свою жизнь со строительством или благоустройством территорий. Чтобы обновить после зимы элементы архитектуры городского парка и закрасить дефекты абстрактных скульптур, не нужно вспоминать сложные уравнения, достаточно применить знание геометрических формул.
К примеру, для правильного нахождения веса декоративного камня, предназначенного для окантовки части клумбы, нужно уметь быстро посчитать размер полуокружности на поверхности ландшафта. Затем необходимо определиться с ценой и принять решение, какой камень можно покупать с учетом сметы. Аналогичная задача возникает при строительстве альпийской горки. Тяжесть камня обеспечит круговую укладку, это свойство позволит высадить декоративные растения в запланированных местах сечения, придав конструкции форму трапеции.
Что представляет собой часть клумбы? Это сектор геометрической фигуры. Внешняя его часть — окантовка клумбы — чаще всего представляет собой дугу окружности. Существует две методики вычисления этой величины:
- градусная (с привязкой к центральному углу);
- по формуле Гюйгенса (с использованием хорды).
Определение методики расчета в полевых условиях зависит от наличия инструментов и особенностей рельефа местности. Но сначала немного теории. Дугой называют часть окружности, расположенную между двумя произвольными точками, находящимися на ней.
Для удобства рассмотрим пример с двумя точками A и B, расположенными на окружности на небольшом расстоянии друг от друга. Они делят её на 2 части — большую и меньшую. Каждая из них называется дугой окружности.
Градусная мера
Длина дуги между точками окружности является функцией центрального угла, образованного радиусами круга (см. рисунок) в прямо пропорциональной зависимости. На этом основана градусная мера.
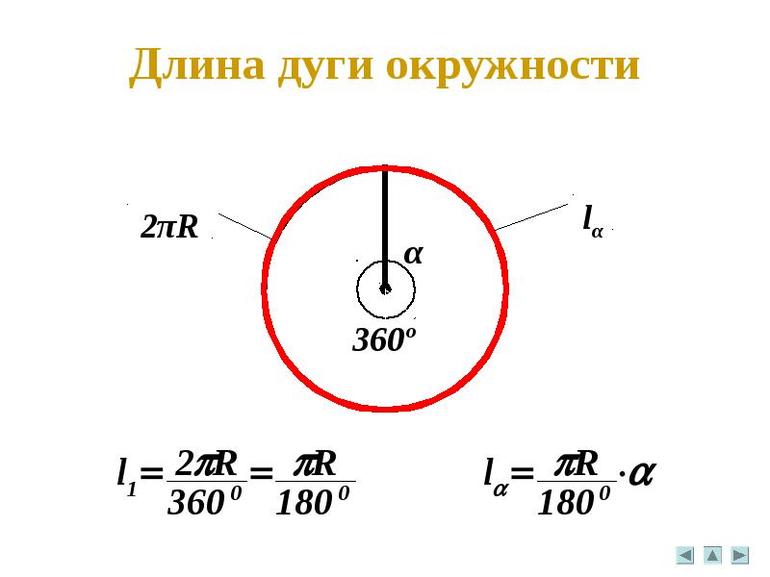
За 1° дуги принимают часть окружности.
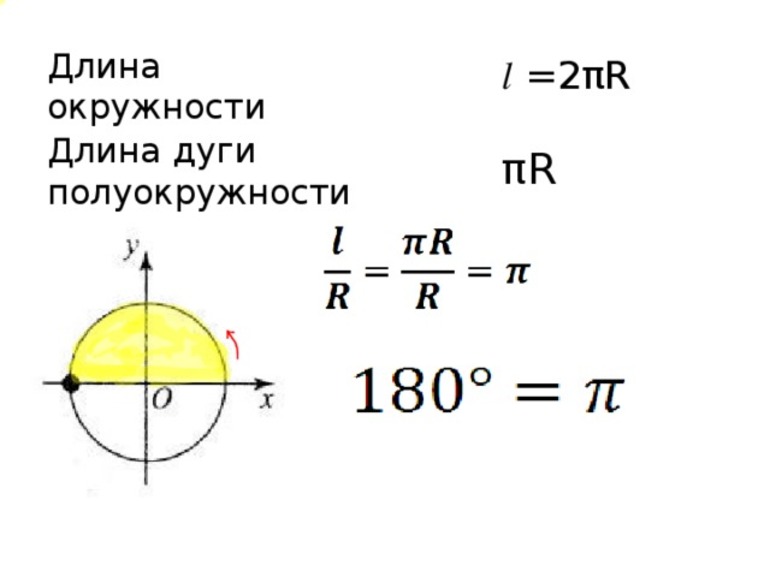
Поскольку L равна , то развернутому углу 180° будет соответствовать длина дуги .
Если значение угла равно 1°, формула выглядит так: .
Следовательно, формула длины дуги окружности с центральным углом n° будет выражаться следующим образом: .
Определим значение l для угла 120° с радиусом, равным 5 мм: l=3,14*30*5/180=2,62 мм.
Применение хорды и высоты
Существует методика расчета длины дуги по хорде и высоте перпендикуляра. Она получила название формулы Гюйгенса. Хорда представляет собой часть прямой, расположенной внутри окружности. Проходящая через центр хорда называется диаметром.
Формулу Гюйгенса применяют, если центральный угол меньше 60 градусов. Для проведения вычислений необходимо сначала соединить точки окружности прямой линией. Это будет хорда. Далее нужно провести перпендикуляр из ее середины, а из точки соприкосновения перпендикуляра с дугой начертить две прямые линии к концам хорды.
Получился равнобедренный треугольник, стороны которого обозначим l , а саму хорду назовем L . Для углов более 60 градусов формулу Гюйгенса не стоит использовать, поскольку при расчетах может возникнуть ошибка. Чем больше угол, тем значительней будет погрешность.
Замерив хорды L и l, можно получить значение дуги, обозначенной на рисунке синим цветом. Если L равна 30 мм, а l — 20 мм, то Р=2*20+3,33=43,33 мм.
Теперь, когда существует понимание методики расчета, можно воспользоваться онлайн-калькулятором. Этот инструмент хорош для проверки полученного экспериментальным путем результата, особенно при обработке большого количества данных, когда необходимо быстро получить ответ.
Онлайн-калькулятор позволяет сохранять полученные значения в буферной памяти компьютера. Оформить данные в виде произвольной таблицы или графика в системе координат не составит труда. Длина дуги окружности по онлайн-калькулятору считается с использованием любой из двух формул: либо по градусной мере, либо по хорде и высоте. Образно говоря, эти формулы являются синонимами, они взаимозаменяемы.
Практика с задачами
Нужно сказать несколько слов об изучении геометрии в средних классах общеобразовательной школы. Существует категория учащихся, для которых формулы сложны для восприятия. Таким ученикам требуется наглядный материал.
На уроке геометрии при изучении материала по вычислениям параметров окружности можно провести практическое занятие. Для этого следует предварительно подготовиться: сделать небольшой чертеж-проекцию гимнастического кольца. Цель занятия — научиться использовать формулы в процессе работы. Ход урока:
- Попросить дежурного ученика принести из спортивного зала гимнастическое кольцо (хула-хуп) небольшого диаметра.
- Отметить фломастером или цветным мелком 3 точки на наружной стороне кольца. После этого оно окажется поделенным на несколько секторов.
- Сделать проекцию кольца на школьной доске с нанесенными точками. На чертеже обозначить центр круга, провести диаметр. Затем нужно соединить отмеченные на окружности точки радиусами с центром круга и хордами между собой.
- Провести все замеры. Получить значения всех параметров и записать на доске. Её предварительно разделить на две части: в центре, доступном для обзора, будут значения центральных углов АОВ и ВОС, диаметр, длина прямых линий АВ, ВС и АС.
- Ответы (искомые значения) записать в правой части доски и прикрыть шторкой до момента окончания практического занятия.
Далее следует разделить класс на 4 небольших группы. Каждой из них нужно дать задание по проведению вычислений с использованием изученных формул.
- группа №1 вычисляет длину дуги между точками А и В, используя градусную меру центрального угла АОВ;
- вторая группа получает аналогичное задание для отрезка между точками В и С;
- третья группа вычисляет искомый параметр между точками А и С, используя длину хорды АС и вспомогательных линий АВ и ВС;
- группа №4 работает с точками А и С, применяя значения угла АОС.
На выполнение задания отводится 12 минут. После истечения времени от каждой из четырех групп выходит ученик, поясняет формулу и записывает на доске полученный результат. Эти ответы сравниваются с уже готовыми замерами, записанными ранее на правой стороне доски.
Следующие 7 минут урока отводятся на обсуждение полученного результата и анализа возникновения погрешности.
Усложнение формулы
Группе продвинутых учеников предлагается задание «Как изменить градусную формулу?». Можно ли найти значение радиуса, используя другие геометрические выражения, например, представить его как половину диаметра круга? В этом случае формулы будет выглядеть следующим образом: r=1/2d, тогда l= πd/360*n.
Если использовать формулу вычисления площади круга и выразить радиус через неё, тогда можно получить s=πr 2 .
Обозначаться радиус будет интересно — в виде производной квадратного корня. Вывести формулу нетрудно, это станет прекрасной ментальной гимнастикой для учащихся.
Базовая цель уроков математики — развитие аналитического мышления учащихся достигается в процессе обсуждения и сравнения различных методик расчета. В качестве дополнительного задания можно предложить ученикам посчитать значение кривой линии наружного края школьной клумбы. Затем следует попросить обосновать свои расчеты.
Использование наглядности поможет учащимся подружиться с формулами, увидеть роль геометрии в повседневной практической жизни и облегчить усвоение конкретного материала.
Источник
Длина дуги
Дифференциальная геометрия кривых — раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами.
Содержание
Способы задания кривой
Наиболее общий способ задать уравнение пространственной кривой — параметрический:
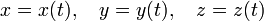 | (1), |
где 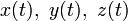
Часто удобно использовать инвариантную и компактную запись уравнения кривой с помощью вектор-функции:
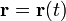
где в левой части стоит радиус-вектор точек кривой, а правая определяет его зависимость от некоторого параметра t . Раскрыв эту запись в координатах, мы получаем формулу (1).
В зависимости от свойств дифференцируемости функций 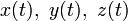
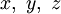
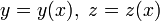
где y(x) и z(x) — дифференцируемые функции.
Для того чтобы точка кривой, заданной общим уравнением (1), была обыкновенной (не особой точкой), достаточно, чтобы в этой точке выполнялось вышеуказанное неравенство
Дифференциальная геометрия рассматривает также кусочно-гладкие кривые, которые состоят из гладких участков, разделённых особыми точками. В особых точках определяющие функции либо не удовлетворяют условиям регулярности, либо вообще не дифференцируемы.
Плоские кривые
Важный класс кривых представляют плоские кривые, то есть кривые, лежащие в плоскости. Плоскую кривую также можно задать параметрически, первыми двумя из трёх уравнений (1). Другие способы:
- Явное задание: y = f(x) .
- Неявное задание:
.
Функции 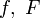
Приведём примеры особых точек для плоских кривых.
- Полукубическая парабола:
Обе производные равны нулю в начале координат. Это особая точка (точка возврата первого рода), в ней вектор касательной скачкообразно меняет направление на противоположное.
- Уравнение (x − 1)(x 2 + y 2 ) = 0 определяет кривую, состоящую из прямой x = 1 и изолированной особой точки в начале координат.
- Лемниската Бернулли — особая точка при самопересечении. В особой точке функция дифференцируема, однако условие регулярности нарушено.
Соприкосновение
Ряд основных понятий теории кривых вводится с помощью понятия соприкосновения множеств,которое состоит в следующем. Пусть M и m — два множества с общей точкой O . Говорят, что множество M имеет с m в точке O соприкосновение порядка 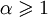
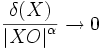
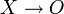
где δ(X) — расстояние точки X множества M от m .
В применении к кривым это означает следующее: две кривые в общей точке имеют степень касания не ниже k-го порядка, если их производные в общей точке, до k-го порядка включительно, совпадают.
Касательная
Если в качестве M взять кривую, а в качестве m прямую, проходящую через точку O кривой, то при 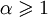
Гладкая регулярная кривая в каждой точке имеет определённую касательную. Направление касательной в точке t0 кривой, задаваемой уравнениями (1), совпадает с направлением вектора 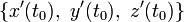
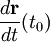
В дифференциальной геометрии выводятся уравнения касательной для различных способов аналитического задания кривой. В частности, для кривой, задаваемой уравнениями (1), уравнения касательной в точке, отвечающей значению параметра t0 , будут
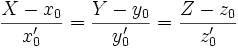
где индекс 0 указывает на значение функций x,y,z и их производных в точке t0 .
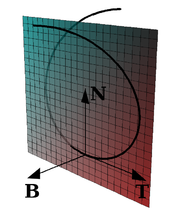
Для плоской кривой уравнение касательной в точке 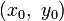
- Параметрическое задание:
- Явное задание: Y = y0 + f0‘(X − x0)
- Неявное задание:
Соприкасающаяся плоскость и нормали
Если взять в качестве m плоскость, проходящую через точку O кривой M , то условие соприкосновения при 
Пусть 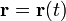
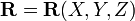
В координатах оно имеет вид:
Прямая, перпендикулярная касательной и проходящая через точку касания, называется нормалью к кривой. Плоскость, перпендикулярная касательной в данной точке кривой, называется нормальной плоскостью; все нормали для данной точки лежат в нормальной плоскости. Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью, а нормаль, перпендикулярная соприкасающейся плоскости, называется бинормалью.
Векторное уравнение бинормали в точке, отвечающей значению t0 параметра t , имеет вид:
Направление главной нормали может быть получено как двойное векторное произведение: 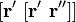
Для плоской кривой содержащая её плоскость совпадает с соприкасающейся. Нормаль, с точностью до знака, только одна — главная, и её уравнение в точке 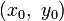
- Параметрическое задание:
- Явное задание:
- Неявное задание:
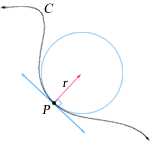
Соприкасающаяся окружность
Для точки кривой вводится важное понятие соприкасающейся окружности. Это окружность, имеющая с кривой соприкосновение порядка 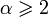
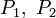
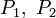
Центр соприкасающейся окружности называют центром кривизны, а радиус — радиусом кривизны. Радиус кривизны является величиной, обратной кривизне (см. ниже). Центр соприкасающейся окружности всегда лежит на главной нормали; отсюда следует, что эта нормаль всегда направлена в сторону вогнутости кривой.
Геометрическое место центров кривизны кривой называется эволютой. Кривая, ортогонально пересекающая касательные кривой, называется эвольвентой. Построение эволюты и эвольвенты — взаимно обратные операции, то есть для эвольвенты данной кривой эволютой является сама кривая.
Длина дуги кривой
Для измерения длины участка (дуги) произвольной кривой эта кривая заменяется ломаной, содержащей точки кривой как точки излома, и максимум длин всех таких ломаных принимается за длину кривой (рис. 3). В инвариантном виде формула для вычисления длины дуги (спрямления кривой) имеет вид:
То же в декартовых координатах:
В полярных координатах для плоской кривой:
Параметризация
Кривая допускает бесчисленное множество различных способов параметрического задания уравнениями вида (1). Среди них особое значение имеет так называемая естественная параметризация, когда параметром служит длина дуги кривой, отсчитываемая от некоторой фиксированной точки.
Среди преимуществ такой параметризации:
имеет единичную длину и поэтому совпадает с ортом касательной.
по длине совпадает с кривизной, а по направлению — с главной нормалью.
Кривизна
При движении вдоль кривой её касательная меняет направление. Скорость этого вращения при равномерном, с единичной скоростью, движении вдоль кривой называется кривизной кривой. В случае параметрического задания кривой уравнениями (1) кривизна кривой определяется по формуле
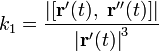
где 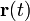
Прямые и только прямые имеют всюду равную нулю кривизну. Поэтому кривизна наглядно показывает, насколько (в данной точке) кривая отличается от прямой линии: чем ближе кривизна к нулю, тем это отличие меньше. Кривизна окружности радиуса R равна 1 / R .
Дважды дифференцируемая кривая в каждой точке, где кривизна отлична от нуля, имеет единственную соприкасающуюся плоскость.
Для плоских кривых можно различать направление вращения касательной при движении вдоль кривой, поэтому кривизне можно приписывать знак в зависимости от направления этого вращения. Кривизна плоской кривой, задаваемой уравнениями 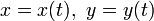
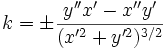
Знак + или — берётся по соглашению, но сохраняется вдоль всей кривой.
Кручение
При движении вдоль кривой в окрестности заданной точки соприкасающаяся плоскость вращается, причём касательная к кривой является мгновенной осью этого вращения. Скорость вращения соприкасающейся плоскости при равномерном, с единичной скоростью, движении называется кручением. Направление вращения определяет знак кручения.
Трижды дифференцируемая кривая в каждой точке с отличной от нуля кривизной имеет определённое кручение. В случае параметрического задания кривой уравнениями (1) кручение кривой определяется по формуле
здесь ( * , * , * ) обозначает смешанное произведение. В координатах:
Для прямой кручение не определено, поскольку неоднозначно определяется соприкасающаяся плоскость. Плоская кривая в каждой точке имеет кручение, равное нулю. Обратно, кривая с тождественно равным нулю кручением — плоская.
Формулы Френе
Фигура, составленная из касательной, главной нормали и бинормали, а также из трех плоскостей, попарно содержащих эти прямые, называют естественным трёхгранником (трёхгранником Френе, см. рис. 4). Соприкасающаяся и нормальная плоскости уже упоминались; третья плоскость, содержащая касательную и бинормаль, называется спрямляющей.
Если рёбра естественного трёхгранника в данной точке кривой принять за оси прямоугольной декартовой системы координат, то уравнение кривой в естественной параметризации раскладывается в окрестности этой точки в ряд по координате вдоль кривой:
где k1 и k2 — кривизна и кручение кривой в указанной точке.
Единичные векторы 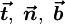
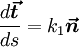 | (2) |
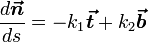 |
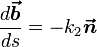 |
где дифференцирование идёт по дуге кривой. Формулы (2) называют формулами Френе́, или Френе-Серре.
Кинематическое истолкование
Будем рассматривать длину дуги заданной кривой как время, а трёхгранник Френе — как твёрдое тело, движущееся вдоль кривой. Тогда это движение в каждый момент времени состоит из поступательного (вдоль касательной) и мгновенного вращения с угловой скоростью 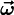
Это означает, что вектор мгновенного вращения лежит в спрямляющей плоскости и распадается на 2 составляющие: вращение вокруг бинормали со скоростью k1 (поворот) и вращение вокруг касательной со скоростью k2 (кручение).
Натуральные уравнения кривой
Кривая с отличной от нуля кривизной полностью определяется (с точностью до положения в пространстве) заданием её кривизны и кручения как функций дуги s кривой. В связи с этим систему уравнения
называют натуральными уравнениями кривой.
Пример
Рассмотрим винтовую линию (рис. 4), заданную уравнениями:
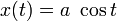
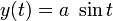
По вышеприведенным формулам получаем:
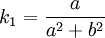
Таким образом, кривизна и кручение винтовой линии постоянны. Поскольку натуральные уравнения однозначно определяют форму кривой, других кривых с постоянными кривизной и кручением не существует. Предельными случаями винтовой линии являются окружность (она получается при b = 0 ) и прямая ( a = 0 ).
См. также
Литература
- Погорелов А. И.Дифференциальная геометрия (6-е издание). М.: Наука, 1974.
- Рашевский П. К.Курс дифференциальной геометрии (3-е издание). М.-Л.: ГИТТЛ, 1950.
Wikimedia Foundation . 2010 .
Полезное
Смотреть что такое «Длина дуги» в других словарях:
длина дуги — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN arc length … Справочник технического переводчика
длина дуги протектора — [ГОСТ 22374 77] Тематики шины пневматические Обобщающие термины параметры пневматических шин EN tread arc width DE Laufflächenbreite FR largeur développée … Справочник технического переводчика
Длина дуги кривой — Дифференциальная геометрия кривых раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами. Содержание 1 Способы задания кривой 1.1 Плоские… … Википедия
Длина кривой — (или, что то же, длина дуги кривой) в метрическом пространстве числовая характеристика протяжённости этой кривой[1]. Исторически вычисление длины кривой называлось спрямлением кривой (от лат. rectificatio, спрямление). Если длина кривой… … Википедия
длина — ы; ж. 1. Протяжение чего л.; расстояние между кем , чем л. Меры длины. Измерить длину и ширину. Д. отрезка прямой. Д. пути. Д. судоходного канала. Во всю длину. Длиною в три метра. 2. Продолжительность, длительность (о времени). Д. рабочего дня.… … Энциклопедический словарь
ДЛИНА — 1) Длина отрезка прямой расстояние между его концами.2) Длина ломаной сумма длин ее звеньев.3) Длина дуги кривой предел длины вписанной в нее ломаной, когда число ее звеньев неограниченно возрастает, причем длина каждого звена стремится к нулю … Большой Энциклопедический словарь
ДЛИНА — числовая характеристика протяженности линий в метрич. пространстве. Д. отрезка прямой расстояние между его концами, измеренное каким либо отрезком, принятым за единицу Д. Длина ломаной сумма Д. ее звеньев. Д. простой дуги точная верхняя грань… … Математическая энциклопедия
ДЛИНА — числовая характеристика протяженности линий в метрич. пространстве. Д. отрезка прямой расстояние между его концами, измеренное каким либо отрезком, принятым за единицу Д. Длина ломаной сумма Д. ее звеньев. Д. простой дуги точная верхняя грань… … Математическая энциклопедия
ДЛИНА ПУТИ — точки длина дуги участка траектории, пройденного точкой за рассматриваемый промежуток времени … Большой энциклопедический политехнический словарь
Дуги-Оток — хорв. Dugi Otok … Википедия
Источник

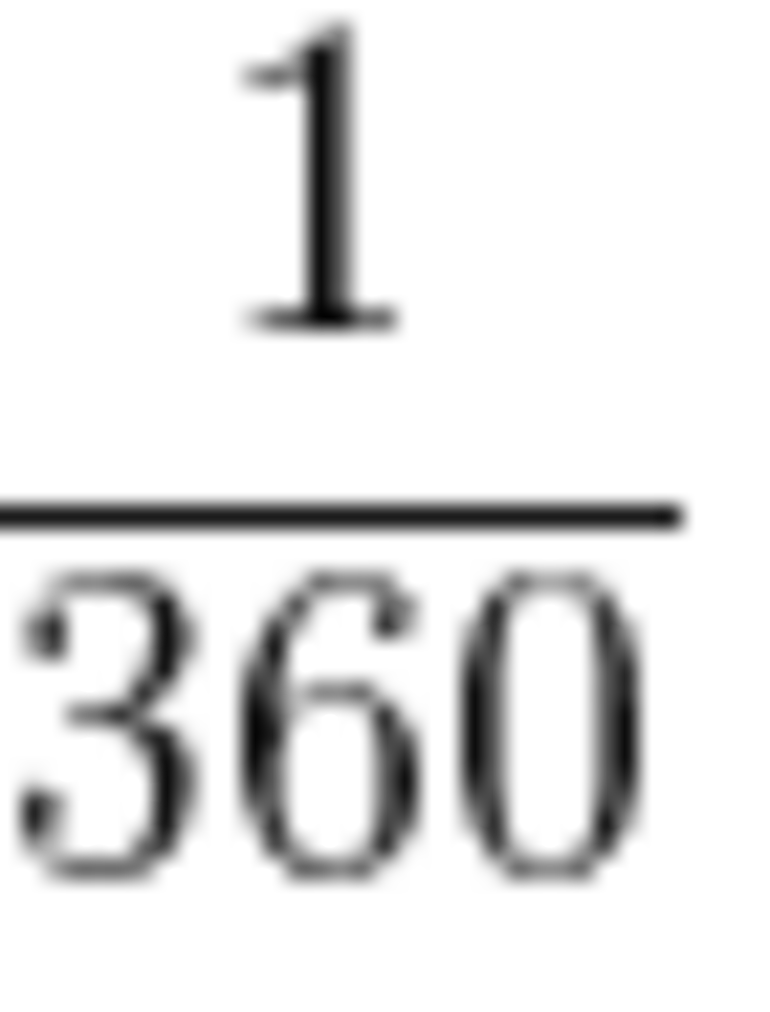
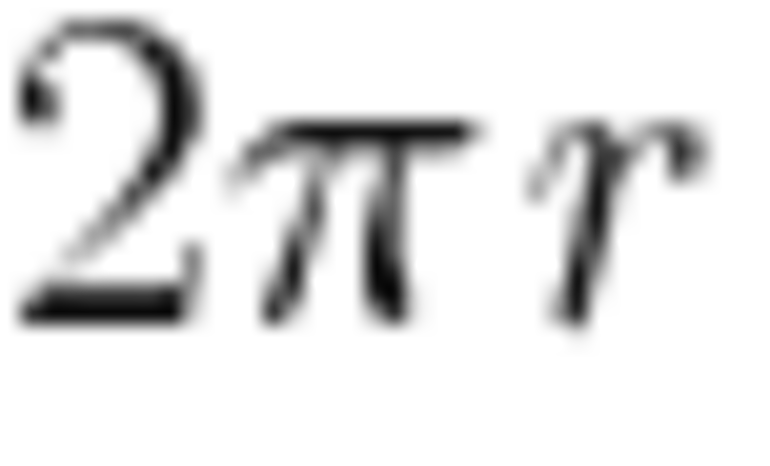
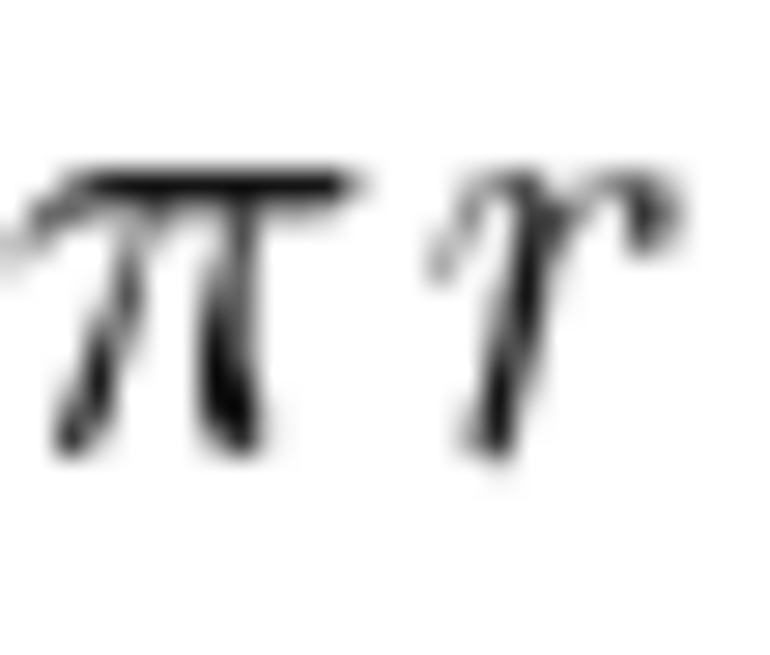
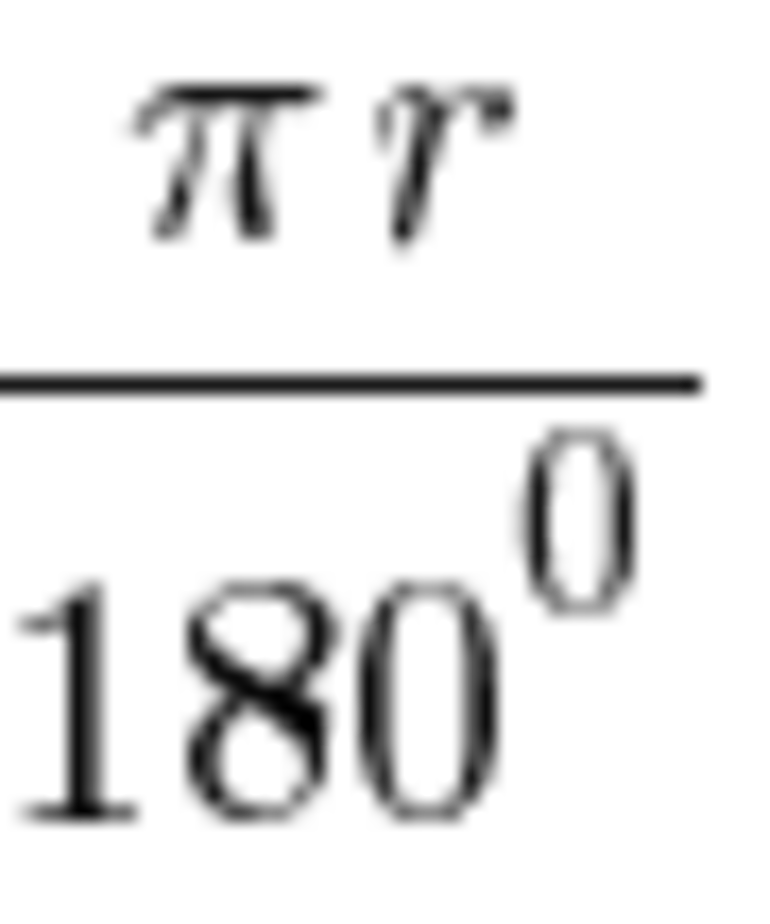
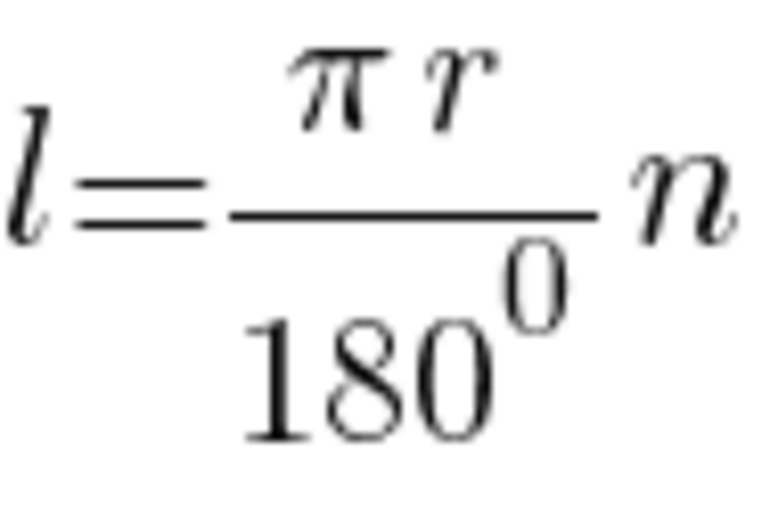
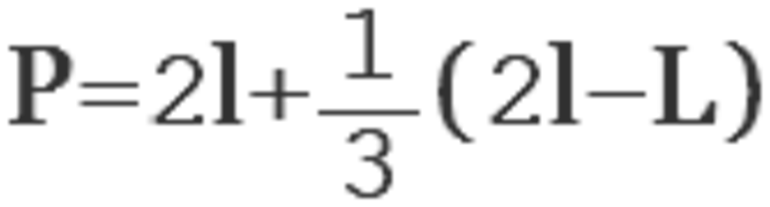

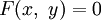 .
.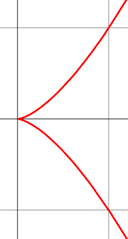
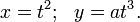 Обе производные равны нулю в начале координат. Это особая точка (точка возврата первого рода), в ней вектор касательной скачкообразно меняет направление на противоположное.
Обе производные равны нулю в начале координат. Это особая точка (точка возврата первого рода), в ней вектор касательной скачкообразно меняет направление на противоположное.
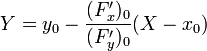
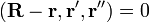
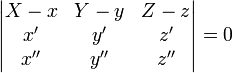
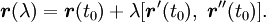
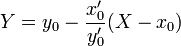
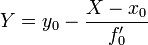
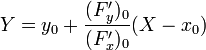

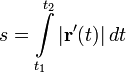
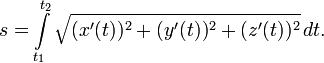
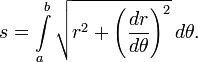
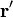 имеет единичную длину и поэтому совпадает с ортом касательной.
имеет единичную длину и поэтому совпадает с ортом касательной.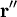 по длине совпадает с кривизной, а по направлению — с главной нормалью.
по длине совпадает с кривизной, а по направлению — с главной нормалью.