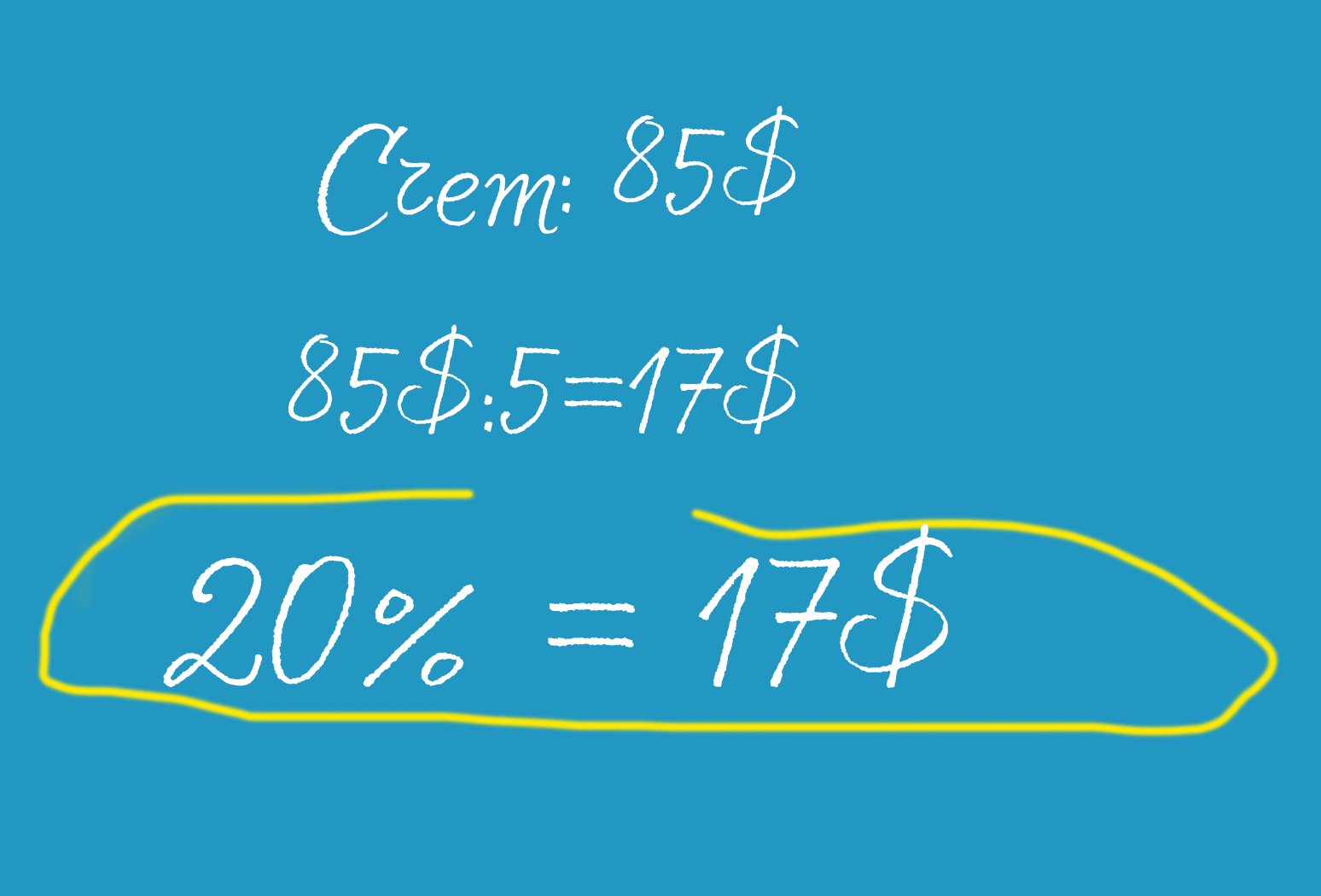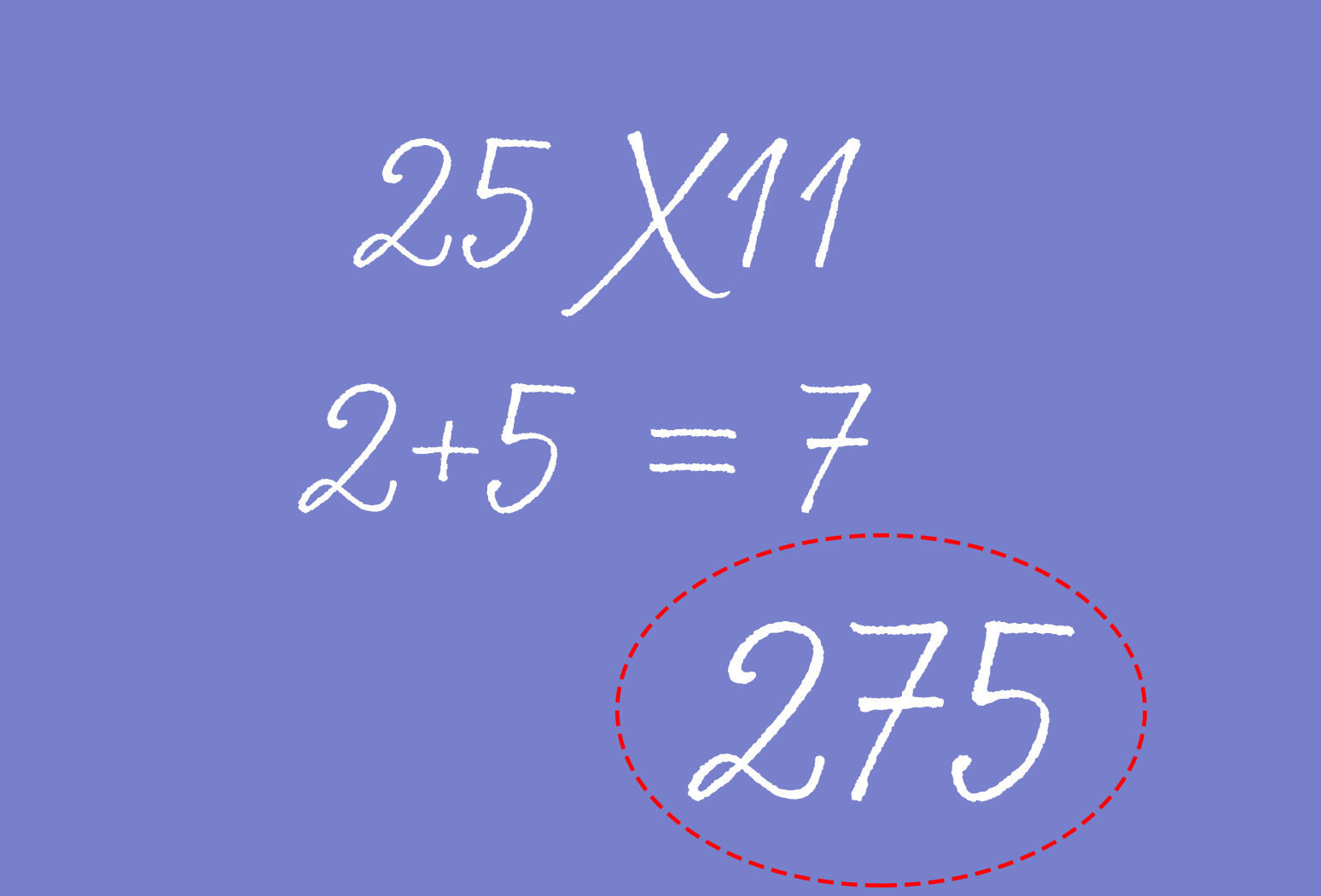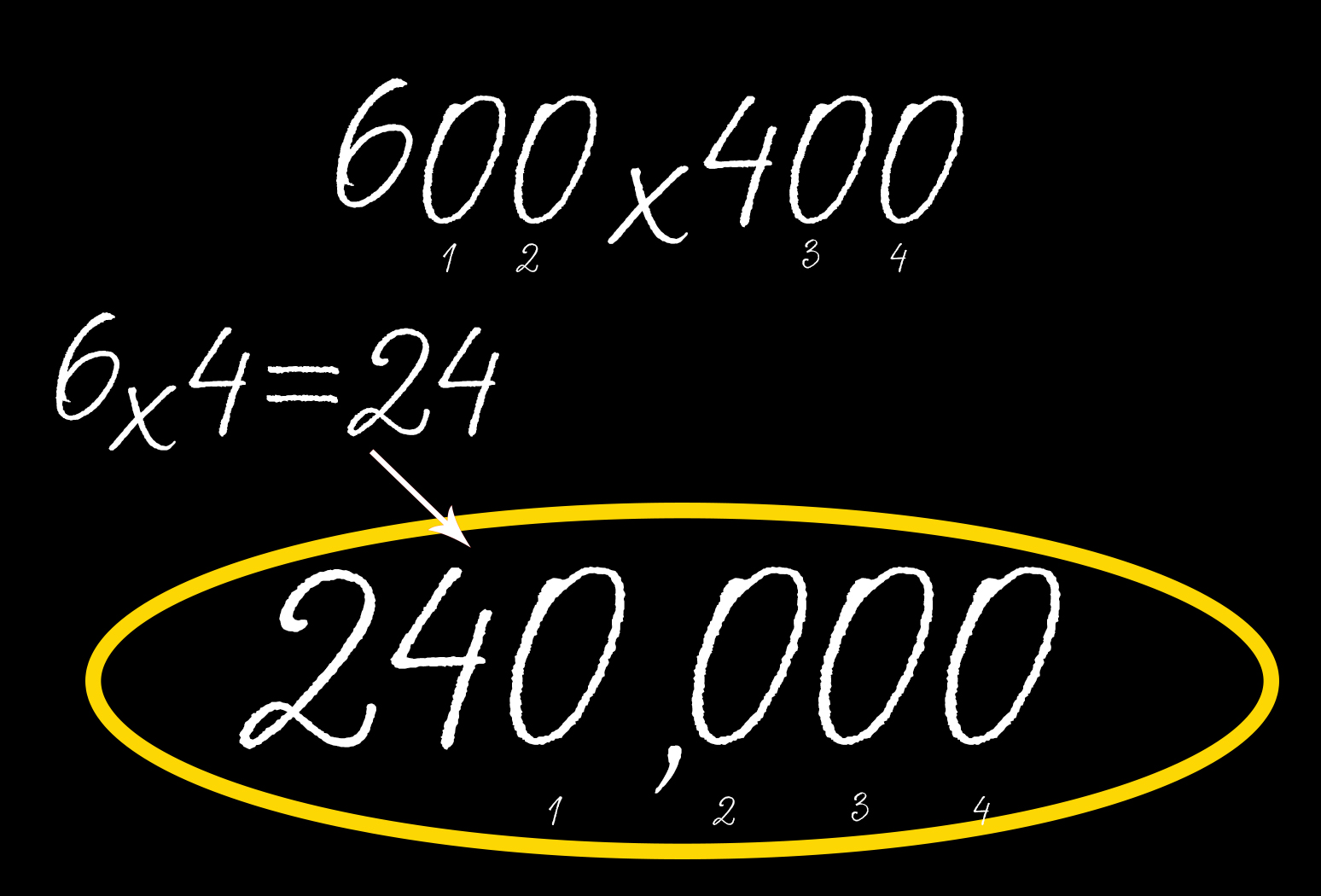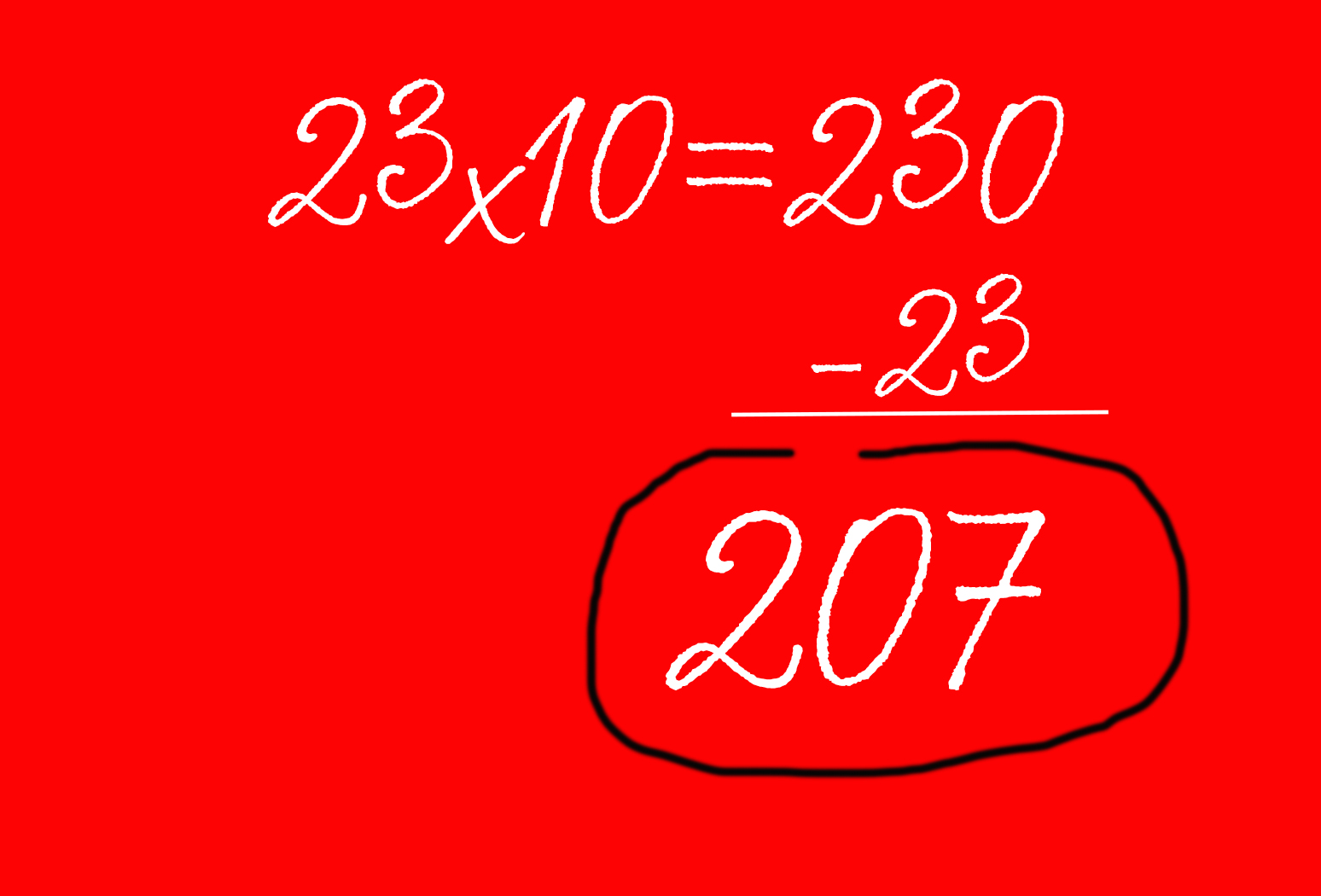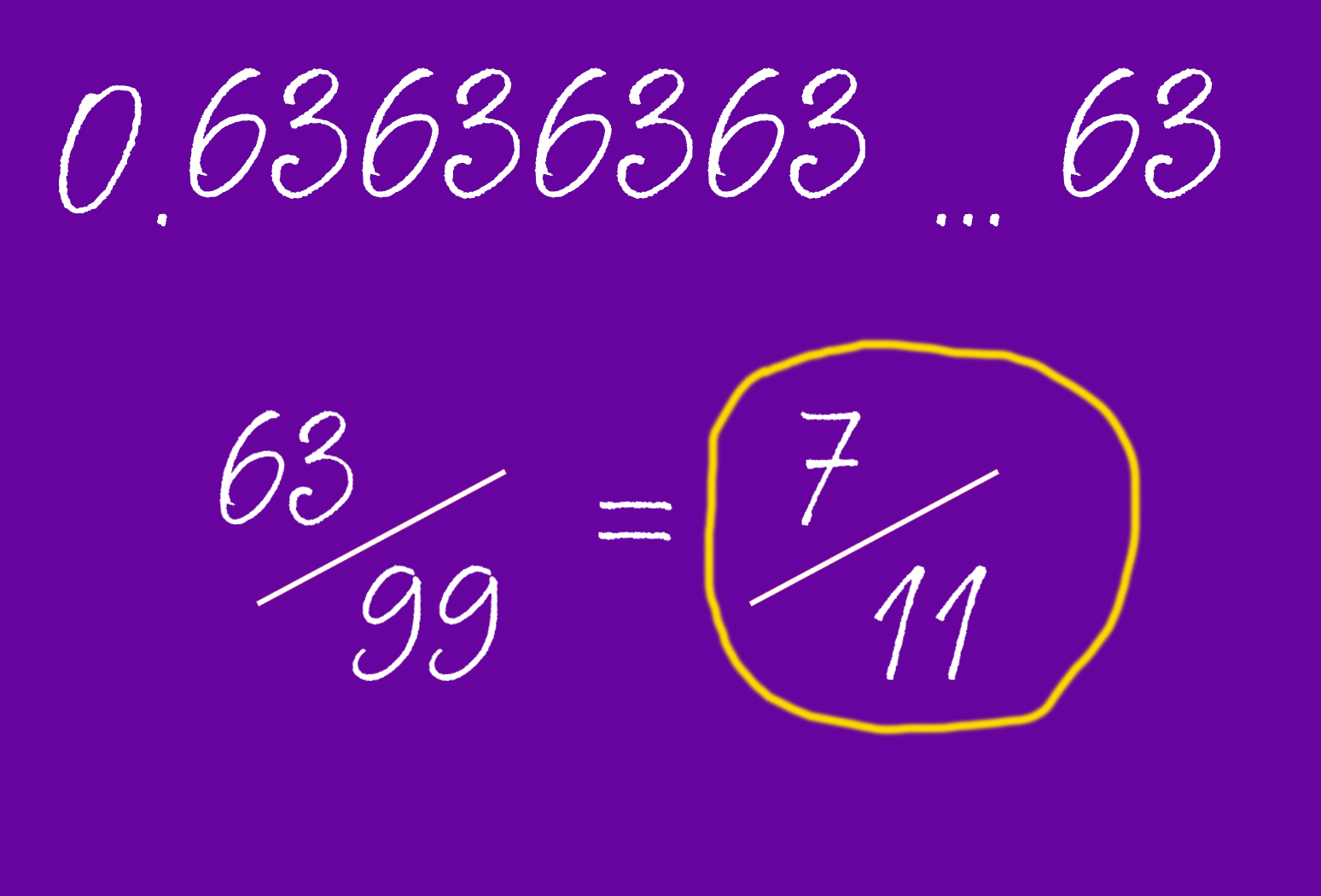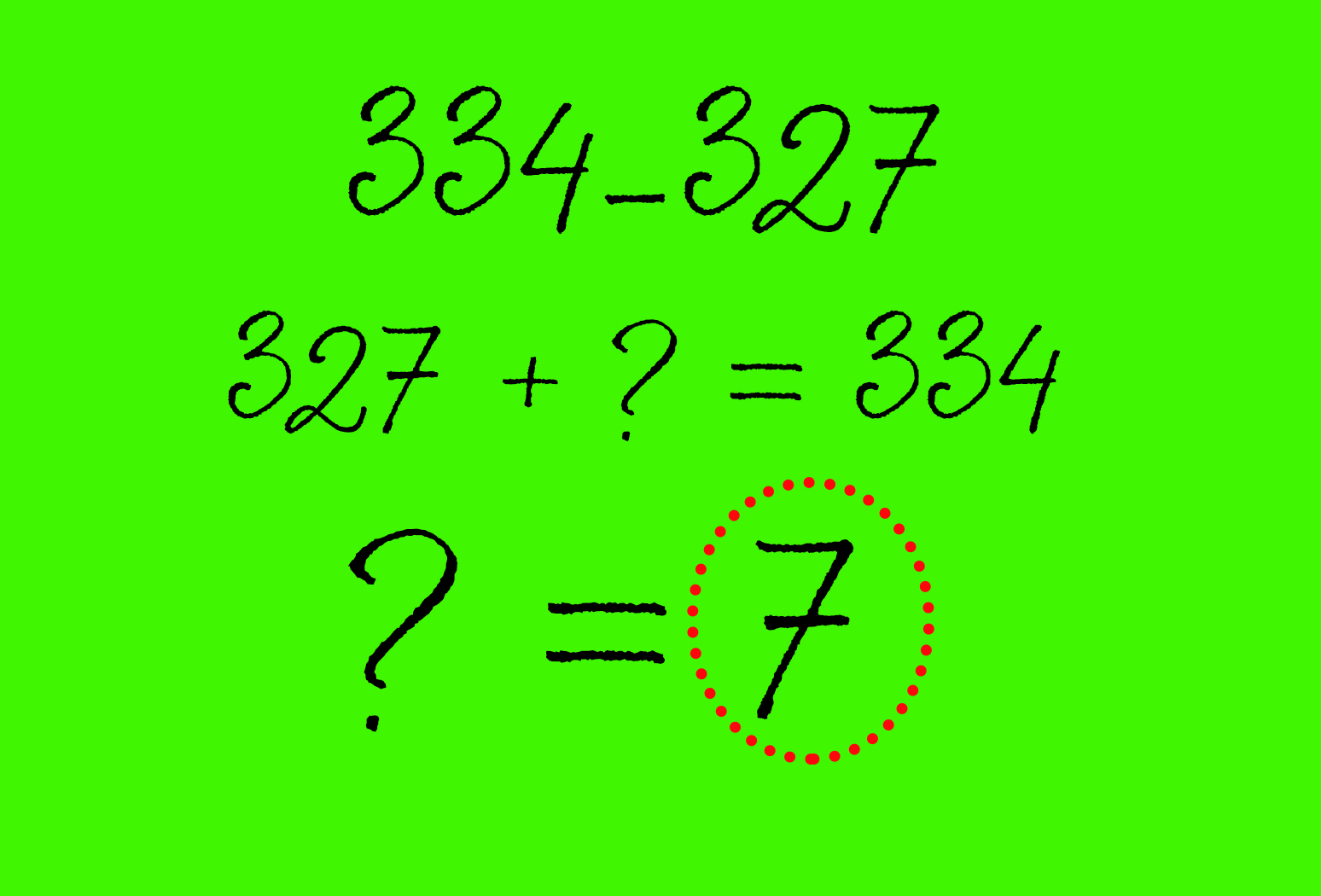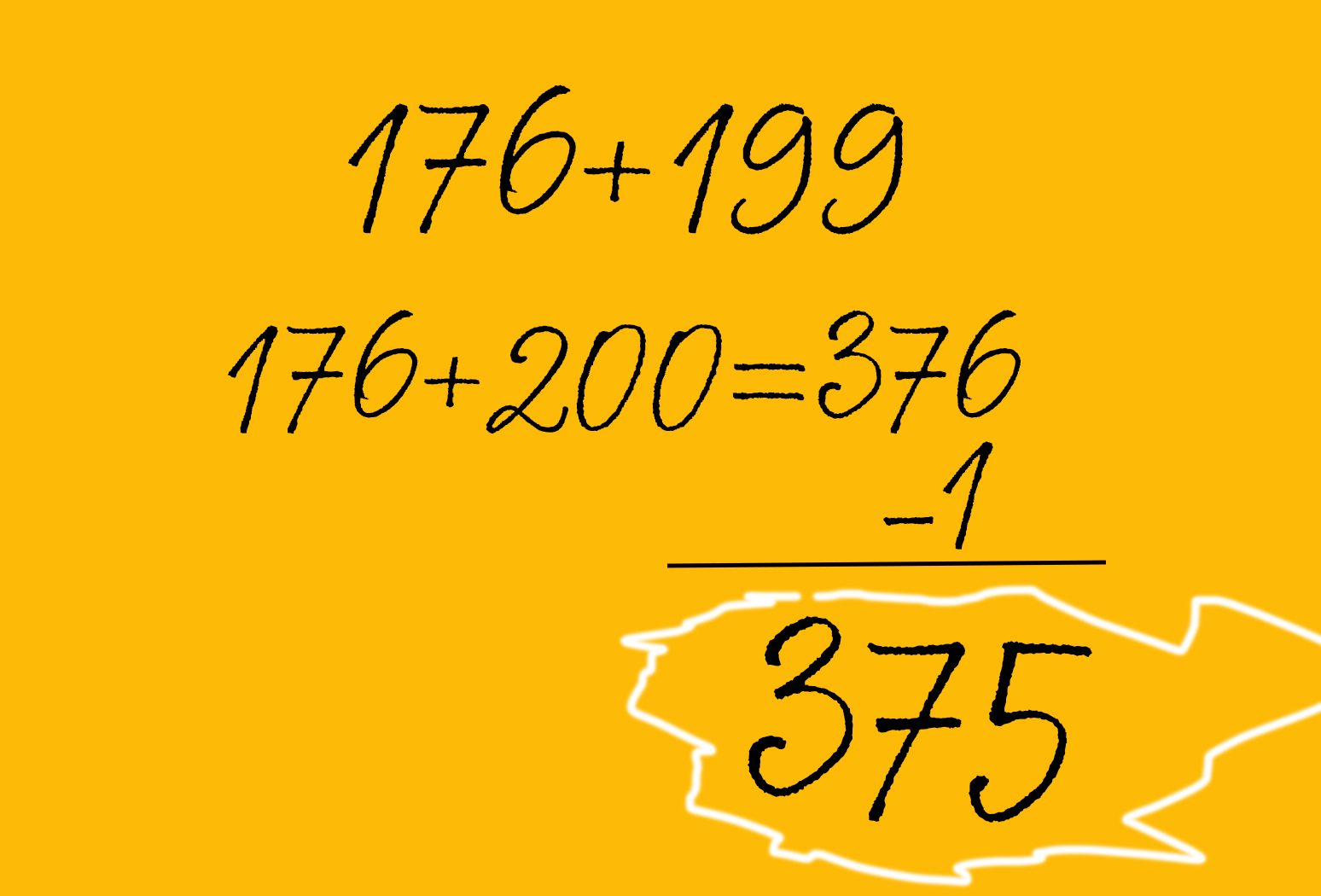Как найти удобный способ вычисления

Долой калькулятор: 12 простых трюков, которые помогут вам быстро считать

Просто, как дважды два.

Как бы мы ни хотели это признавать, учителя были правы: математика нужна каждому из нас. Но далеко не всем дается ловкое жонглирование числами. Тогда на помощь приходят легко запоминающиеся математические приемы – настоящее спасение, когда под рукой, как назло, нет калькулятора.

Ниже вы найдете 12 способов быстрых вычислений для всех, кто далек от точных наук.

1. Быстрое вычисление 20%

Представим, что границы вновь открыли и первым делом вы отправились в США. А там принято оставлять на чай. Обычно размер чаевых составляет 15-20% от суммы вашего заказа.

По словам Кейт Сноу, автора серии книг The Math Facts That Stick, чтобы быстро вычислить 20% от суммы, вам нужно просто разделить число в чеке на 5.

Например, вы поели на 85 долларов. Разделите 85 на 5, и у вас получится 17 долларов – чаевые, которые вы должны оставить официанту.

2. Умножение двузначных чисел на 11

Умножить число на 11 очень легко с помощью хитрого трюка от math.hmc.edu. Просто сложите две цифры и поместите полученную сумму в середину числа.

Например, вы умножаете 25 на 11. Если сложить 2 и 5, получится 7. Теперь расположите 7 между 2 и 5, чтобы найти окончательный ответ – 275.

3. Быстрое удвоение

Чтобы удвоить большое число, умножьте каждую цифру на 2 и сложите их между собой. Кейт Сноу предлагает начинать слева – так будет легче.

«Чтобы удвоить, к примеру, 147, начните с разряда сотен. Если умножить 100 на 2, получится 200. 40 на 2 – 80. 7 на 2 – 14. Теперь сложите числа между собой (200 + 80 + 14), и вы получите 294», – объясняет Сноу.

4. Умножение чисел, которые оканчиваются на ноль

Примеры с большими пугающими числами, которые оканчиваются на ноль, тоже легко решить с помощью специального приема. Согласно education.cu-portland.edu, нужно просто «вычеркнуть» нули из примера, а в конце вновь их добавить.

Если вы умножаете 600 на 400, уберите все нули и перемножьте 6 на 4. Получится 24. Затем подсчитайте общее количество нулей в исходном уравнении и припишите их к полученному значению. Так как в нашем примере было четыре нуля, то ответ будет равен 240000.

5. Умножение на 9

Если вам так и не удалось выучить таблицу умножения – не переживайте. По словам Сноу, чтобы легко умножить число на 9, нужно умножить его на 10 и вычесть исходное число из полученного значения.

Например, вам нужно умножить 9 на 23. Для этого умножаем 23 на 10 и получаем 230. А затем вычитаем из него 23, чтобы получить окончательный ответ – 207.

6. Деление на 10, 100 или 1000

Разделить число на 10 проще простого – согласно Сноу, «нужно просто переместить десятичный знак на одну позицию влево от исходного числа, чтобы найти ответ».

Для деления на 100 применим тот же метод, за исключением одного – нужно переместить десятичный разряд на две позиции левее исходного числа. Что касается деления на 1000, просто переместите десятичный знак на три позиции влево.

Например, если вы делите 42,94 на 10, вы просто перемещаете десятичный знак на одну позицию влево и получаете 4,294.

7. Умножение на 10, 100 или 1000

Здесь все работает с точностью до наоборот. Чтобы умножить число на 10, переместите десятичный знак на одну позицию вправо. На 100 – на две позиции. На 1000 – на три позиции.

Например, если вам нужно умножить 366,78 на 100, передвиньте десятичный знак на две цифры вправо, чтобы получить ответ 36678.

8. Преобразование периодической десятичной дроби в обыкновенную

Согласно businessinsider.com, нужно выполнить всего 3 шага, чтобы легко превратить бесконечную десятичную дробь в обыкновенную, с числителем и знаменателем.

• Шаг 1. Найдите повторяющиеся цифру или число. Например, у 0,636363 это будет 63.
• Шаг 2. Определите, сколько разрядов в этом числе. В нашем случае у 63 – два разряда.
• Шаг 3. Разделите повторяющееся число на число с таким же количеством разрядов, которое будет состоять из одних девяток – в данном случае 99. Получим 63/99. Теперь сократим ее и получим 7/11 – наш ответ.

9. Умножение на 25

Умножать на 25 не так уж и сложно, если представлять число в виде дроби 100/4. В этом случае все, что вам нужно сделать, это разделить число на 4 и умножить на 100.

Например, вам нужно умножить 84 на 25. Сначала делим 84 на 4 – получаем 21, а потом умножаем значение выражения на 100. Ответ: 2100.

10. Возведение чисел, оканчивающихся на 5, в квадрат

«Этот математический трюк подразумевает 2 шага», – объясняет Сноу. Чтобы возвести в квадрат число, которое оканчивается на пять, возьмите первую цифру числа и умножьте ее на себя. После этого прибавьте к полученному результату первую цифру и припишите к ответу 25. Кружится голова? Разберем на примере.

Если вы умножаете 35 на 35, сначала умножьте 3 на 3 – получится 9, – и прибавьте 3 к ответу – получится 12. Теперь припишите 25 в конец найденного числа, и вы найдете окончательный ответ: 1225.

11. Вычитание путем сложения

Если вам кажется, что сложение немного проще, чем вычитание, этот трюк для вас. Когда вам нужно найти разность двух чисел, достаточно близких друг к другу, попробуйте решить пример с помощью сложения.

«Вместо того чтобы пытаться вычесть 327 из 334, представьте это в виде суммы: мол, сколько нужно добавить к 327, чтобы получить 334?» – объясняет Сноу.

12. Сложение чисел, оканчивающихся на 99

Если вы пытаетесь прикинуть, во сколько обойдутся продукты, стоимость которых заканчивается на 99, – калькулятор не нужен. Все, что необходимо сделать, – прибавить 100 вместо 99, а потом вычесть единицу.

Сноу объясняет этот процесс на примере 176 + 199 = 375. «Если к 176 мы прибавим 200, то получим 376, – говорит эксперт. – Поскольку вы добавили на единицу больше, чем вам нужно, вычтите ее из 376, чтобы найти правильный ответ: 375».

Источник

Математика. 3 класс

Конспект урока

Математика, 3 класс

Урок № 57. Разные способы вычислений.

Перечень вопросов, рассматриваемых в теме:

Как выполнять устно вычисления в случаях, сводимых к действиям в пределах 1000, используя различные приёмы устных вычислений?

Как выбирать удобный способ?

Как выполнять проверку вычислений?

Глоссарий по теме:

Круглым называется число, которое делится на 10, 100, 1000 и так далее, без остатка.

Каждая цифра в записи многозначного числа занимает определённое место – позицию. Место (позицию) в записи числа, на котором стоит цифра, называют разрядом.

Единицы, десятки, сотни, тысячи и т. д. иначе ещё называют разрядными единицами:
единицы называют единицами 1-го разряда
десятки называют единицами 2-го разряда
сотни называют единицами 3-го разряда и т. д.

Сложение – арифметическое действие в математике, в результате которого два или более чисел объединяется в единое целое, оно обозначается знаком «+». Слагаемое, слагаемое, сумма – главные составляющие математического действия сложения.

Вычитание – арифметическое действие, обратное сложению и обозначается оно знаком «-». Уменьшаемое, вычитаемое, разность- главные составляющие математического действия вычитания.

Основная и дополнительная литература по теме урока:

Моро М.И. Учебник для 3 класса четырехлетней начальной школы. М. «Просвещение» — 2017. С. 68-69

Волкова С.И. математика. Проверочные работы. 3 кл. — М.: Просвещение, 2018.С. 72-73

Рудницкая В.Н. Математика. Дидактические материалы. Ч.1. 3 кл. – М. «Вентана- Граф», 2016, с. 9-12

Теоретический материал для самостоятельного изучения

Вам уже знакомы приёмы устных вычислений в пределах 1000.

Но наша цель не просто узнать о них, а уверенно ими пользоваться.

Часто ученики допускают ошибки при решении примеров.

Сегодня мы более подробно остановимся на таких случаях и разберемся, как их избежать

Надеюсь, что после урока вы даже сможете посоревноваться с друзьями в устном счёте.

Вспомним приёмы устных вычислений, с которыми познакомились на прошлом уроке.

работаем с разрядными слагаемыми

работаем с общим количеством десятков.

Чтобы быстро и правильно решать такие примеры надо уметь выбирать более удобный способ.

А как выбрать удобный способ?

Выберем из этих примеров те, которые удобнее решать, работая с разрядными слагаемыми.

Согласитесь, что эти примеры будет легко решить, представив одно из слагаемых в виде суммы разрядных слагаемых.

Например: 420 + 50, десятки сложим с десятками и прибавим сотни, а при решении примера 320 + 500 сложим сотни и прибавим десятки.

Что же не так с остальными примерами?

Внимательно посмотри на числа. При выполнении действий с десятками происходит переход через разряд. Это вызывает затруднения.

Именно поэтому здесь удобнее воспользоваться вторым способом – работать с общим количеством десятков.

Рассмотрим первый пример: 150 — 90

Пользуясь первым способом, нам пришлось бы из 50 вычитать 90, а это невозможно.

Приходит на помощь второй способ:

15 дес. — 9 дес. это 6 дес. или 60. Никаких проблем.

Тоже самое с остальными примерами.

Но есть ещё одна опасность при решении подобных примеров на вычитание.

Рассмотрим два примера:

560 — 300 и 600 — 240.

Обрати внимание, в первом примере десятки в уменьшаемом, а во втором — в вычитаемом.

На это очень важно обращать внимание!

Понаблюдаем за решением.

560 — 300 = (500 — 300) + 60 = 260

600 — 240 = (600 — 200) — 40 = 360

В первом случае десятки прибавляем, а во втором вычитаем. Так как в первом случае вычитаем только сотни – 300, а во втором – сотни и десятки — 240

Если же ты сомневаешься в результате или просто хочешь убедиться в правильности, можно выполнить проверку.

Проверка выполняется обратным действием. Сложение проверяем вычитанием и наоборот.

Проверка: 260 + 300 = 560

Проверка: 360 + 240 = 600

Сегодня мы раскрыли вам секреты приёмов устного сложения и вычитания.

Пользуйтесь ими и удачи!

Задания тренировочного модуля:

1. Распределите карточки с примерами на две группы по более удобному способу решения.

1. Поставьте в ячейке напротив «+», если согласны с решением, и «-», если не согласны.

1. Ученик решил примеры. Выберите отметку, которую он получил за работу.

Источник

Применение рациональных приёмов вычислений — путь к развитию логического мышления..

«Мозг хорошо устроенный ценится больше,

чем мозг хорошо наполненный!»

Развитие логического мышления младших школьников – одна из главных целей уроков математики. Эту цель учитель ставит не только при обучении решению задач, но и при формировании вычислительных навыков. Владение навыками устных вычислений в пределах 100 является культурой математики и в некоторой степени показателем сформированности логического мышления. Правильно организованная деятельность учащихся, приведёт к формированию у них логического мышления.

Что же понимается под «логическим мышлением»? Оно понимается как способность и умение ребёнка младшего школьного возраста самостоятельно производить простые логические действия (анализ, синтез, сравнение, обобщение и др.), а также составные логические операции (построение отрицания, утверждение и опровержение как построение рассуждения с использованием различных логических схем – индуктивной или дедуктивной). Практика показывает, что простые логические действия в определённой мере формируются у каждого человека стихийно, хотя следует отметить, что специально организованная работа в этом направлении резко повышает уровень их сформированности. Составные логические операции, имеющие более сложный и комплексный характер, у большинства людей сами по себе не формируются, их развитие требует специальной методической работы. Период дошкольного и младшего школьного возраста является наиболее благоприятным для того, чтобы стимулировать и развивать простые логические действия. В дальнейшем эта база поможет организовать специальную работу по формированию составных логических операций: обучению рассуждениям и способам доказательства в среднем звене обучения. При этом, умениям, на практике часто возникает интересный психологический резонанс: специальная работа с ребёнком приводит к активному проявлению у него интеллектуальных способностей, он легко начинает схватывать общую суть вопроса или приёма действия.

Очевидна необходимость целенаправленной работы по формированию логического мышления школьников в начальном звене обучения именно на уроках математики, являющейся одним из основных предметов обучения, в котором формируется логическое мышление ребёнка. Как же определены приоритеты по данному вопросу в разных образовательных системах? Сравним две программы образовательного компонента «Математика» в начальной школе:

1. «Школа России». Программа «Математика» (М.И.Моро, М.А.Бантова, Г.В.Бельтюкова, С.И.Волкова, С.В.Степанова. Под редакцией Ю.М.Колягина): «В курсе математики заложен механизм формирования у детей сознательных и прочных навыков устных и письменных вычислений, доведения до автоматизма знания табличных случаев действий. Усилена линия развивающих и занимательных упражнений».

Одна из важнейших задач обучения младших школьников математике в «Школе России»- формирование у них вычислительных навыков, основой которых является осознанное и прочное усвоение приёмов устных и письменных вычислений. Современный комплект математики для начальной школы («Школа России») содержит упражнения для развития логических приёмов умственных действий (сравнение, обобщение, синтез, анализ, классификация и др.). Однако эти упражнения часто воспринимаются учителями как упражнения тренировочного характера с целью прочного усвоения учениками вычислительных навыков. Выполнение большого количества однотипных упражнений способствует усвоению вычислительного приёма, но и вместе с тем снижает познавательную активность детей, интерес к процессу, рассеивает внимание, что приводит к увеличению ошибок и никоим образом не формирует логическое мышление. Значит, есть необходимость использования системы упражнений с определённой целью, а именно: развитие логических приёмов умственных действий.

2. «Школа 2100». Программа «Математика» (Г.В.Дорофеев, Г.К.Муравин, Л.Г.Петерсон): «Учебный комплект по математике сориентирован на развитие мышления и творческих способностей ребёнка, его интереса к математике, обеспечивает возможность разноуровневого обучения, реализует концепцию современной массовой школы….»

В условиях развивающего обучения («Школа 2100») система упражнений направлена на усвоение вычислительных умений и навыков. Она ставит цель: формировать обобщённые способы действий, побуждать учащихся к самостоятельному поиску новых способов действий, рассмотрению нескольких способов решения задания и оцениванию их с точки зрения рациональности.

Использование рациональных приёмов помогает значительно облегчить процесс вычислений, способствует формированию положительных мотивов к этому виду деятельности. Поэтому работа по поиску рациональных приёмов вычислений должна проводиться постоянно, систематически и в тесной связи с программным материалом.

Методика преподавания математики в начальных классах раскрывает теоретические основы рациональных приёмов вычислений, связанных с выполнением разных математических действий с натуральными числами. Рациональные приёмы сложения основываются на коммуникативном и ассоциативном законах сложения, а также на свойствах изменения суммы.

Рассмотрим подробнее введение этих приёмов, при изучении действий сложения и вычитания:

1. Рациональные приёмы сложения основываются на законах и свойствах действия сложения.

Коммуникативный закон сложения. Сумма не изменяется от перемены мест слагаемых.

а + в = в + а 4 + 18 = 18 + 4

Ассоциативный закон сложения. Сумма не изменится, если заменить какую-либо группу рядом стоящих слагаемых их суммой.

(а + в) + с = а + (в + с) 26 + 3 + 17 = 26 + (3 + 17) = 46

Свойство 1.1. Если одно из слагаемых увеличить или уменьшить на некоторое число, то сумма, соответственно, увеличится или уменьшится на это число.

Если а + в + с = S , то (а + к) + в + с = S + к Если 38 + 24 + 15 = 87, то 40 + 24 + 15 = ?

Если а + в + с = S , то (а – к) + в + с = S — к Если 38 + 24 + 15 = 87, то 36 + 24 + 15 = ?

Свойство 1.2. Если одно из слагаемых увеличить, а другое уменьшить на одно и то же число, то сумма не изменится и, наоборот, если одно из слагаемых уменьшить, а другое увеличить на одно и то же число, то сумма не изменится.

Если а + в = S , то (а + к) + (в – к) = S Если 56 + 27 = 83, то 59 + 24 = ?

Если а + в = S , то (а – к) + (в + к) = S Если 56 + 27 = 83, то 54 + 29 = ?

Приём 1.1. Округление одного или нескольких слагаемых. Одно (или несколько слагаемых) заменяют ближайшим к нему «круглым» числом и находят сумму «круглых» чисел. Затем соответствующее дополнение (дополнения) до «круглого» числа прибавляют к полученной сумме или вычитают из неё. Например:

14 + 28 = (14 + (28 + 2)) – 2 = (14 + 30) – 2 = 44 – 2 = 42

57 + 32 = (57 + (32 — 2)) + 2 = (57 + 30) + 2 = 87 + 2 = 89

48 + 39 = ((48 + 2) – 2) +((39 + 1) – 1) = (50 + 40) – 3 = 87

63 + 28 =((63 – 3) + 3) + ((28 + 2) – 2) = (60 + 30) + 3 – 2 = 90 + 3 – 2 = 91

Приём 1.2. Поразрядное сложение. При сложении нескольких многозначных чисел сначала находят суммы соответствующих разрядных единиц всех чисел, а затем складывают полученные суммы. Например:

26 + 17 +35 + 23 = (20 + 10 + 30 + 20) + (6 + 7 + 5 + 3) = 80 + 21 = 101

Приём 1.3. Группировка вокруг одного и того же «корневого» числа. Например:

Пусть требуется найти сумму чисел: 26 + 24 + 23 + 25 + 24
Легко заметить, что все эти числа близки к повторяющемуся дважды числу 24, поэтому его можно считать «корневым» числом, а искомую сумму вычисляют следующим образом:

Находят сумму «корневых» чисел: 24 + 24 + 24 + 24 + 24 = 24 5 = 120

Находят сумму отклонений (выясняют, как каждое число отличается от «корневого»): 2 + 0 — 1 + 1 + 0 = 2

Получившуюся сумму прибавляют к первому результату: 120 + 2 = 122

Проверить результат можно, взяв «корневым» числом другое, например, наименьшее число 23.

Выполним вычисление по вышеуказанным пунктам:

23 + 23 + 23 + 23 + 23 = 23 5 = 115

3 + 1 + 0 + 2 + 1 = 7

Естественно, предлагается и другой способ проверки, когда «корневым» числом будет наибольшее число 26. Выполним вычисления:

26 + 26 + 26 + 26 + 26 = 26 5 = 130

0 – 2 – 3 — 1 – 2 = — 8

Прибавим алгебраически результаты: 130 + (- 8) = 122

Вывод: выбор «корневого» числа не влияет на результат. (Данный приём целесообразно рассматривать во внеурочное время или на уроках закрепления изученного материала при изучении умножения многозначных чисел на однозначное число.)

2. Все приёмы рациональных вычислений, связанных с вычитанием, основываются на законах вычитания, правилах вычитания числа из суммы и суммы из числа, свойствах изменения разности.

Свойство 2.1. Если уменьшаемое увеличилось или уменьшилось на некоторое число, то разность соответственно увеличится или уменьшится на это число.

Если а – в = с, то (а + к) – в = с + к Если 74 – 28 = 46, то 77 – 28 = ?

Если а – в = с, то (а – к) – в = с – к Если 74 -28 = 46, то 72 – 28 = ?

Свойство 2.2. Если вычитаемое увеличить или уменьшить на несколько единиц, то разность изменится на столько же единиц, но в противоположную сторону.

Если а – в = с, то а – (в + к) = с – к Если 56 – 24 = 32, то 56 – 27 = ?

Если а – в = с, то а – (в – к) = с + к Если 56 – 24 = 32, то 56 – 22 = ?

Свойство 2.3. Если уменьшаемое и вычитаемое увеличить или уменьшить на одно и то же число, то разность не изменится.

Если а – в = с, то (а + к) – (в + к) = с Если 87 – 24 = 63, то 89 – 26 = ?

Если а – в = с, то (а – к) – (в + к) = с Если 87 – 24 = 63, то 85 – 22 = ?

Приём 2.1. Увеличение или уменьшение уменьшаемого и вычитаемого на одно и то же число. Например:

56 – 28 = (56 + 2) – (28 + 2) = 58 – 30 = 28

82 – 27 = (82 – 2) – (27 – 2) = 80 – 29 = 51

(Эти приёмы особенно актуальны, когда вычитаемое или уменьшаемое близки к «круглому» числу)

Приём 2.2. Округление вычитаемого. Вычитаемое заменяют ближайшим к нему «круглым» числом, находят разность, а затем соответствующее дополнение до «круглого» числа прибавляют к полученной разности или вычитают из неё. Например:

93 – 28 = 93 – (28 + 2) = (93 – 30) + 2 = 63 + 2 = 65

71 – 42 = 71 – (42 – 2) = (71 – 40) – 2 = 31 – 2 = 29

В полной мере предусматривается знакомство с приёмами рациональных вычислений в программе «Школа 2100». Они рассматриваются после изучения приёмов сложения и вычитания на отдельных уроках. В учебнике «Математика 2 кл.» (М.И.Моро и др.) в УМК «Школа России» так же предлагаются задания, основанные на свойствах сложения и вычитания. Однако в них нет требования «сравнить, не выполняя действий», «не производя вычислений» и т.п. Учителю необходимо нацеливать учеников при их выполнении на применение рациональных приёмов вычислений, на выявление закономерностей, формируя при этом логическое мышление. При формировании у школьников вычислительных навыков, работая по традиционной программе, я уделяю большое внимание рациональным приёмам вычислений. Приведу примеры, которые предлагаю детям на уроках в качестве разминки или как дополнительный материал. Выше (при рассмотрении рациональных приёмов вычислений) так же приведены некоторые примеры.

1. Вычисли удобным способом, определи, какое правило ты использовал:

7 + 8 + 3 + 2 18 + 11 + 22 + 19 65 + 9 +5 4 + 8 + 76

2. Поставь знаки сравнения, не выполняя вычислений, и докажи, что они поставлены правильно:

6 + 4 * 6 + 3 (свойство 1.1) 6 – 3 * 6 – 4 (свойство 2.2)

2 + 7 * 3 + 7 8 – 2 * 7 – 2 (свойство 2.1.)

— На сколько одно выражение больше другого?

3. Сравни числовые выражения, не выполняя вычислений, и объясни, как ты рассуждал

23 + 16 * 20 + 19 (свойство 1.2.)

4. Выполняется ли данное правило при вычитании? Проверь вычислением:

5. Объясни, как найти сумму и разность, пользуясь свойствами сложения и вычитания:

36 + 12 = 38 + 10 = …(свойство 1.2.) 14 + 28 = (14 + 30) – 2 = …(приём 1.1.)

36 – 12 = 34 – 10 =… (свойство 2.3.) 42 + 29 = (40 + 29) + 2 =…(приём 1.1)

6. Выполни действия. Как изменилась разность? Почему?

82 –16 74 – 9 (свойство 2.1)

51 – 17 63 – 45 (свойство 2.2.)

7. Реши примеры. Что ты замечаешь?

60 – 3 60 – 13 60 – 23 60 – 33

8. Объясни приём вычисления:

73 – 19 = 74 – 20 = 54 (свойство 2.3.)

— Продолжи решение примеров:

9. Объясни решение примеров:

14 + 28 = (14 + 30) – 2 = …(приём 1.1.) 48 + 39 = (50 + 40) – 2 – 1 = 90 – 3 =

57 + 32 = (57 + 30) + 2 = 63 + 28 = (60 + 30) + 3 – 2 = 90 + 1 =

42 + 29 = (40 + 29) + 2 =

(При выполнении приёма округления одного или нескольких слагаемых действия проговариваются вслух и запись сокращается.)

Источник