Как найти суммы чисел применяя способ группировки слагаемых

Способ группировки слагаемых

Скачать
презентацию Способ сложения >>

Способ группировки слагаемых. Этот способ применяют в том случае, когда слагаемые при их группировке в сумме дают круглые числа, которые затем складывают между собой. Пример. Найдем сумму чисел 74, 32, 67, 48, 33 и 26. Решение. Суммируем числа, сгруппированные следующим образом:(74 + 26) + (32 + 48) + (67 + 33) = 280.

Слайд 14 из презентации «Рациональный счёт». Размер архива с презентацией 1289 КБ.

Математика 5 класс

«5 класс «Площадь прямоугольника»» — Найдите площади фигур, если длина стороны квадрата 1 см. Площадь квадрата. Площадь квадрата со стороной 1 см. Найдите неизвестные размеры. Формула площади прямоугольника. Найдите площадь и периметр прямоугольника. По какой формуле вычисляется площадь квадрата. Найдите значение выражений. Решите задачу. Решить уравнения. Найдите площадь прямоугольника. Найдите площадь квадрата. Равные фигуры. Укажите порядок действий в выражениях.

«Числовые подстановки в буквенные выражения» — Числовые и буквенные выражения. Поезд. Самостоятельная работа. Буквенные выражения. Точка. Числовые выражения. Точки. Реши задачу. Числовое выражение. Железная дорога. Сколько километров прошёл поезд за двое суток. Выбери выражение. Термометр. Найди значение выражения. Найдите периметр треугольника. Составьте выражение. Заполни таблицу. Поезд шёл двое суток. Температура.

«Математические фокусы» — Таинственная девятка. Извлечение кубического корня. Фокусы. Фокус с шестью квадратиками. Задуманное число. Ход. Возраст. Объяснение. Предметы. Наименьшее число. Последовательность цветов. Зритель. Пластинки. Кусочек бумажки. Буквы. Квадраты. Варианты. Цифры. Цифры куба. Магия. Карточки с числами. Имя и фамилия. Фокусник. Феноменальная память. Прямоугольник. Внутреннее отверстие. Секрет фокуса. Математические фокусы.

«Сложение и вычитание натуральных чисел» — Свойства сложения. Содержание. Прибавить к числу сумму двух. Сложение и вычитание натуральных чисел. Числа, которые складывают, называют слагаемыми. Периметр – это сумма длин сторон многоугольника. От прибавления нуля число не изменяется. От перестановки мест слагаемых сумма не изменяется. Если прибавить к натуральному числу единицу, то получится следующее. Изобразите на координатном луче сложение.

«Задачи на сложение и вычитание дробей» — Вычислительный центр. Остров Смекалистых. Путешествие на поезде. Устранение ошибок. Пересаживаемся в лодку. Вниз по реке. Основные свойства сложения и вычитания. Какое число задумано. Поле Чудес. Десятичные дроби. V течения. Садимся в автобус. Сложение и вычитание десятичных дробей. Движется поезд. Город Угадайка. Много решено загадок. Город. Путешествие.

«Математика в нашей жизни» — Спорт и математика. Кому нужна математика. Правильно спланированный и примененный тренировочный план. При расчетах непременно математика нужна. Академическая гребля. Как воздух, математика нужна, самой отваги офицеру мало. Занятие математикой развивает личность, делает ее целеустремленнее. Есть о математике молва, что она в порядок ум приводит. Математика в жизни. Значение математических дисциплин важно в различных видах спорта.

Всего в теме «Математика 5 класс» 177 презентаций

Источник

Группировка слагаемых

Группировка слагаемых — это объединение слагаемых в группы с помощью скобок. При группировке слагаемых обычно изменяется порядок их следования в сумме для удобства вычислений.

Метод группировки слагаемых можно применять к суммам, состоящим из трёх и более слагаемых. Группировку можно разбить на три последовательных действия:

1. нахождение слагаемых, которые можно объединить в группу;
2. перестановка слагаемых (применение переместительного закона сложения);
3. заключение слагаемых в скобки (применение сочетательного закона сложения).

Рассмотрим нахождение значения выражения, изображённого на картинке:

Можно просто сначала сложить первые два слагаемых, к полученной сумме прибавить третье слагаемое, а к полученному результату затем прибавить четвёртое слагаемое:

15 + 27 + 55 + 13 = 42 + 55 + 13 = 97 + 13 = 110,

но в данном случае значение выражения будет легче найти, если сначала сгруппировать слагаемые так, чтобы в сумме они давали круглые числа:

15 + 27 + 55 + 13 = (15 + 55) + (27 + 13) = 70 + 40 = 110.

Приём группировки слагаемых обычно используется для упрощения вычислений.

Пример. Вычислить значение выражений, используя приём группировки слагаемых.

1) 248 + 123 + 52 + 7;

2) 101 + 67 + 19 + 3;

3) 340 + 114 + 60 + 26;

4) 154 + 235 + 13 + 115 + 46.

1) 248 + 123 + 52 + 7 = ( 248 + 52) + ( 123 + 7) = 300 + 130 = 430;

2) 101 + 67 + 19 + 3 = ( 101 + 19) + ( 67 + 3) = 120 + 70 = 190;

3) 340 + 114 + 60 + 26 = ( 340 + 60) + ( 114 + 26) = 400 + 140 = 540;

4) 154 + 235 + 13 + 115 + 46 = ( 154 + 46) + ( 235 + 115) + 13 = 200 + 350 + 13 = 563.

Источник

Группировка слагаемых и множителей: правило, примеры

В случае, если нам надо сложить три и более слагаемых, мы можем использовать метод тождественного преобразования, получивший название группировки слагаемых. Точно такой же метод существует и для умножения, если в примере заданы три множителя и больше. Целью этой статьи является разбор правил группировки в обоих случаях. Все теоретические положения будут проиллюстрированы примерами решений задач.

Что такое группировка слагаемых

Мы можем выполнять группировку как в буквенных, так и в числовых выражениях тогда, когда у нас есть 3 слагаемых и более. Как нужно понимать этот термин?

Группировка слагаемых основана на совместном рассмотрении нескольких слагаемых в исходной сумме. Иначе говоря, это объединение нескольких слагаемых в одну группу.

Основное правило группировки слагаемых звучит так:

При выполнении группировки мы сначала переставляем слагаемые в исходной сумме таким образом, чтобы слагаемые одной группы были рядом, после чего заключаем их в скобки.

На чем базируется данное правило? В его основе лежат переместительное и сочетательное свойство сложения.

Разберем несколько примеров.

Допустим, у нас есть сумма 3 — х слагаемых 3 + 2 + 1 , и нам нужно сгруппировать первое слагаемое со вторым. Перестановка в данном случае не потребуется, поскольку нужные слагаемые и так стоят рядом. Нам надо только добавить скобки в нужном месте: ( 3 + 2 ) + 1 . Вот и вся необходимая группировка, после которой можно переходить к вычислениям.

Возьмем пример чуть сложнее.

Итак, мы имеем сумму 4 — х слагаемых 1 + 8 + 2 + 9 . Осуществим группировку в данном выражении, объединив первое и последнее, а также второе и третье слагаемое. Для этого нам надо переставить их так, чтобы нужные слагаемые расположились рядом друг с другом: 1 + 9 + 8 + 2 . Все, что нам нужно сделать теперь, это добавить скобки в нужных местах: ( 1 + 9 ) + ( 8 + 2 ) .

Точно так же мы действуем, если вместо числового выражения задано выражение с переменными. Так, если в условии стоит сумма вида x + y 3 + 3 · y 2 + 2 · x 2 + y + 12 , то можно сделать группировку сначала всех слагаемых с x , а потом всех с y . В итоге у нас получится выражение вида ( x + 2 · x 2 ) + ( y 3 + 3 · y 2 + y ) + 12 .

В целом группировка слагаемых– несложное действие. Некоторая трудность может быть в том, чтобы найти в исходном выражении саму сумму и отдельные слагаемые, из которых она состоит, особенно если выражение длинное и громоздкое. После нахождения слагаемых сгруппировать их будет легко.

К примеру, в выражении x + 1 · 1 x — 2 + x 2 + x + 1 4 + 3 · x — 2 3 можно найти три слагаемых: x + 1 · 1 x — 2 , x 2 + x + 1 4 и 3 · x — 2 3 .

После нахождения всех элементов можно объединить в группу первое и третье слагаемое и получить следующее выражение:

x + 1 · 1 x — 2 + 3 · x — 2 3 + x 2 + x + 1 4

Также три слагаемых можно выделить и в дроби x 2 + x + 1 4 . Они расположены под знаком корня. Для них тоже можно провести группировку.

Метод группировки необходим для рационального вычисления значений выражений. Кроме того, он широко используется для упрощения и многих других задач разной степени сложности.

Например, если нам надо найти значение выражения 1 3 + 2 7 + 2 3 + 3 7 , то удобно будет воспользоваться группировкой и объединить дроби с одинаковыми знаменателями. Так вычисление станет проще и быстрее:

1 3 + 2 7 + 2 3 + 3 7 = 1 3 + 2 3 + 2 7 + 3 7 = 1 + 5 7 = 1 5 7

Один из способов разложения многочлена на отдельные множители также основан на группировке слагаемых.

Что такое группировка множителей

Такая группировка проводится точно таким же образом, как и при сложении, единственная разница в том, что работать предстоит не с суммами, а с произведениями. Она основана на переместительном и сочетательном свойствах умножения.

Группировка множителей – это объединение в одну группу нескольких множителей.

Процесс вычисления в данном случае проводится так же: сначала мы переставляем нужные множители так, чтобы они оказались рядом, а потом расставляем скобки.

Например, возьмем произведение 3 · a · 7 · b и выполним группировку отдельно буквенных и числовых множителей. Сначала переставим их, чтобы нужные множители стояли рядом, а затем выделим их скобками. В итоге у нас получится выражение вида ( 3 · 7 ) · ( a · b ) .

Источник

Сумма разрядных слагаемых

О чем эта статья:

Сумма разрядных слагаемых

Любое натуральное многозначное число можно представить в виде суммы разрядных слагаемых. Сумму разрядных слагаемых можно записать следующим образом:

• Число 35 состоит из 3 десятков и 5 единиц

35 = 3 десятка + 5 единиц = 3*10 = 30 + 5 = 35.

30 — разрядное слагаемое; 5 — разрядное слагаемое.

• Число 86 состоит из 8 десятков и 6 единиц

86 = 8 десятков + 6 единиц = 8*10 = 80 + 6 = 86

80 — разрядное слагаемое; 5 — разрядное слагаемое.

• Число 356 состоит из 3 сотен, 5 десятков и 6 единиц

356 = 3 сотни + 5 десятков + 6 единиц = 3*100 + 5*10 + 6 = 300+50+6 = 356.

300, 50, 6 — разрядные слагаемые.

Разряды и классы чисел

Чтобы без труда записывать числа в виде суммы разрядных слагаемых, нужно безошибочно определять класс и разряд числа.

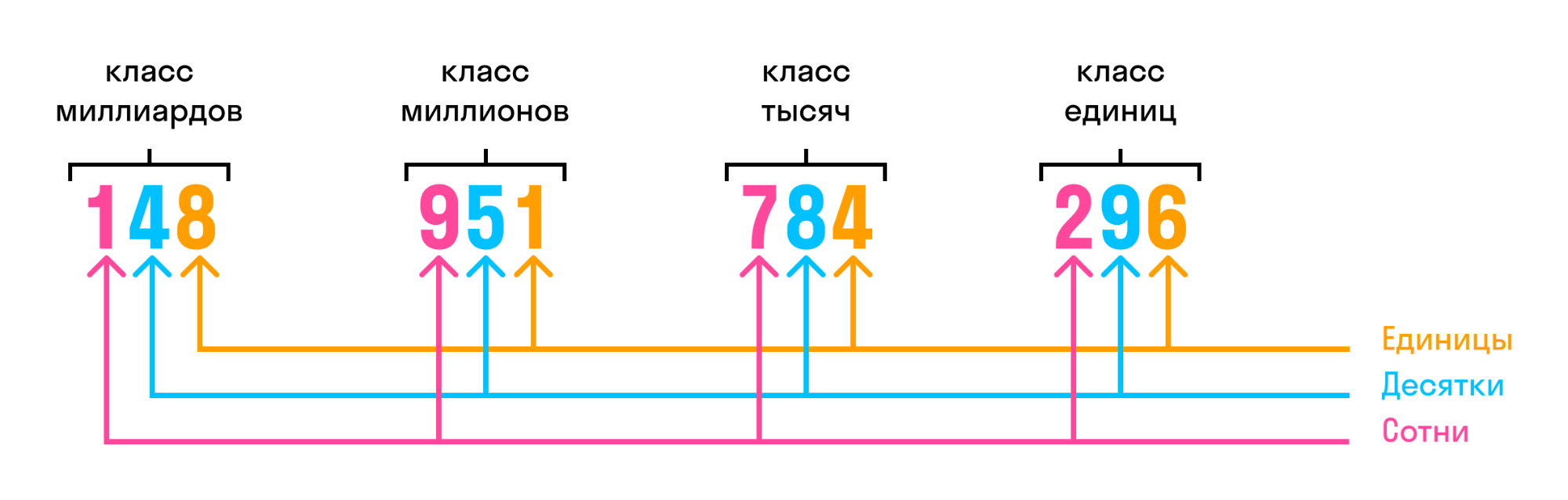
В многозначном числе цифры справа налево разбиваются на группы по три цифры. Такие группы называют классами.

Названия классов многозначных чисел:

• первый — класс единиц,
• второй — класс тысяч,
• третий — класс миллионов,
• четвёртый — класс миллиардов,
• пятый — класс триллионов,
• шестой — класс квадриллионов,
• седьмой — класс квинтиллионов,
• восьмой — класс секстиллионов.

Чтобы чтение многозначного числа не превращалось в головоломку, при записи лучше разграничивать число по классам. Вот так:

• 345 466 129 350 вместо 345466129350

Читаться такое число будет слева направо: триста сорок пять миллиардов четыреста шестьдесят шесть миллионов сто двадцать девять тысяч триста пятьдесят.

Разряд — это место, которое занимает цифра в записи многозначного числа.

Разряды считаются справа налево. Первая цифра справа в записи числа относится к первому разряду.

• Например, в числе 128 656 374 252 разряды считаются справа налево: 2 — первый разряд; 5 — второй разряд; 2 — третий разряд; 4 — четвертый разряд; 7 — пятый разряд; 3 — шестой разряд; 6 — седьмой разряд; 5 — восьмой разряд; 6 — девятый разряд; 8 — десятый разряд; 2 — одиннадцатый разряд; 1 — двенадцатый разряд.

Разрядные единицы — это единицы, десятки, сотни, тысячи, миллионы.

Все разрядные единицы, за исключением простых единиц, — составные единицы. Каждые десять единиц одного разряда составляют одну единицу следующего разряда.

• 10 единиц = 1 десяток;
• 10 десятков = 1 сотня;
• 10 сотен = 1 тысяча;
• 10 тысяч = 1 десяток тысяч;
• 10 десятков тысяч = 1 сотня тысяч;
• 10 сотен тысяч = 1 миллион.

Если составная единица больше другой единицы — она называется единицей высшего разряда. Если меньше, то единицей низшего разряда. Так, например, сотня — единица высшего разряда относительно десятка, но низшего разряда относительно тысячи.

Чтобы выяснить сколько всего в числе единиц определенного разряда, нужно мысленно вычеркнуть из числа все цифры низшего разряда.

• Например, нужно сказать, сколько сотен в числе 5689.

Это значит, нужно выяснить, сколько сотен заключается в тысячах и в сотнях этого числа. 5689 — на третьем месте в классе единиц стоит цифра 6, значит в числе есть 6 сотен. Следующая влево цифра — 5 (тысячи). 1 тысяча = 10 сотен. 5 тысяч = 50 сотен. Всего в числе 56 сотен.

Если в разряде стоит цифра 0, то это означает отсутствие единиц, десятков, сотен и т.д., в зависимости от того, где именно содержится цифра.

Иногда бывает необходимо не только разложить число на разрядные слагаемые, но и определить количество единиц какого-то определенного разряда.

В такой ситуации можете выполнить подробный разбор числа.

• Разберем число 6 057 386

Шесть миллионов пятьдесят семь тысяч триста восемьдесят шесть

6 057 386 = 6 * 1 000 000 + 0 * 100 000 + 5 * 10 000 + 7 * 1000 + 3 * 100 + 8 * 10 + 6 = 6 000 000 + 50 000 + 7 000 + 300 + 80 + 6.

Из чего состоит это число? Из:

• шести единиц миллионов (6 * 1 000 000);
• пяти десятков тысяч (5 * 10 000);
• семи единиц тысяч (7 * 1000);
• трех сотен (3 * 100);
• восьми десятков (8 * 10);
• шести единиц (6).

Для того, чтобы алгоритм разложения числа на простые слагаемые был всегда под рукой, сохраняйте себе табличку с примером. В ней вы найдете вопросы, которые помогут разложите любое число.

Определите, сколько единиц в числе 5 068 252.

1. Определяем сколько всего единиц в числе.

2. Определяем количество десятков.
Записываем число без первого разряда (единицы).

3. Определяем количество сотен.
Записываем число без первого
и второго разрядов (десятки и сотни).

4. Определяем количество единиц тысяч.
Записываем число без первого, второго,
третьего разрядов (единицы, десятки, сотни).

5. Определяем количество десятков тысяч.
Записываем число без первого, второго, третьего,
четвертого разрядов (единицы, десятки, сотни, единицы тысяч).

6. Определяем количество сотен тысяч.
Записываем число без десятков тысяч, единиц тысяч,
сотен и единиц.

7. Определяем количество единиц миллионов.
Записываем число без сотен тысяч, десятков тысяч,
единиц тысяч, сотен, десятков, единиц.

Расписав таким образом число, мы выяснили, что в числе 5 068 252: 5 единиц класса миллионов (3 класс); 68 единиц класса тысяч (2 класс); 252 единицы класса единиц (1 класс).

Может показаться, что такой подробный разбор ни к чему, что и без того все понятно, но многоразрядные многозначные числа — коварны. Лучше хорошенько потренироваться, используя все вспомогательные материалы, как эта табличка, а потом уже раскладывать любое число за секунды и в уме.

Примеры

Внимательно просмотрите примеры и попробуйте самостоятельно представить числа в виде суммы разрядных слагаемых.

Представьте в виде суммы разрядных слагаемых:

1. 84 610
   84 610 = 8 * 10 000 + 4 * 1 000 + 6 * 100 + 10
   84 610 = 80 000 + 4 000 + 600 + 10.
2. 45 317
   45 317 = 4 * 10 000 + 5 * 1000 + 3 * 100 + 17
   45 317 = 40 000 + 5 000 + 300 + 17.
3. 56 789
   56 789 = 5 * 10 000 + 6 * 1000 + 7 * 100 + 8 * 10 + 9
   56 789 = 50 000 + 6 000 + 700 + 80 + 9.
4. 345 677
   345 677 = 3 * 100 000 + 4 * 10 000 + 5 * 1000 + 6 * 100 + 7 * 10 + 7
   345 677 = 300 000 + 40 000 + 5 000 + 600 + 70 + 7.
5. 687 543
   687 543 = 6 * 100 000 + 8 * 10 000 + 7 * 1000 + 5 * 100 + 4 * 10 + 3
   687 543 = 600 000 + 80 000 + 7 000 + 500 + 40 + 3.
6. 877 589
   877 589 = 8 * 100 000 + 7 * 10 000 + 7 * 1000 + 5 * 10 + 8 * 10 + 9
   877 589 = 800 000 + 70 000 + 7 000 + 500 + 80 + 9.

Как видите, все довольно просто. Занятие весьма успокаивающее, медитативное. Приятно сесть после тяжелого дня и пораскладывать числа на разрядные слагаемые.

Если вдруг так вышло, что вы не расслабляетесь при виде цифр, то воспользуйтесь онлайн-калькулятором. В интернете таких калькуляторов немало, вот один из них.

1. 4 895 634
   4 895 634 = 4 * 1 000 000 + 8 * 100 000 + 9 * 10 000 + 5 * 1000 + 6 * 100 + 3 * 10 + 4
   4 895 634 = 4 000 000 + 800 000 + 90 000 + 5 000 + 600 + 30 +4.
2. 8 675 349
   8 675 349 = 8 * 1 000 000 + 6 * 100 000 + 7 * 10 000 + 5 * 1000 + 3 * 100 + 4 * 10 + 9
   8 675 349 = 8 000 000 + 600 000 + 70 000 + 5 000 + 300 + 40 + 9.
3. 77 897 125
   77 897 125 = 7 * 10 000 000 + 7 * 1 000 000 + 8 * 100 000 + 9 * 10 000 + 7 * 1000 + 1 * 100 + 2 * 10 + 5
   77 897 125 = 70 000 000 + 7 000 000 + 800 000 + 90 000 + 7 000 + 100 + 20 + 5.
4. 656 734 212
   656 734 212 = 6 * 100 000 000 + 5 * 10 000 000 + 6 * 1 000 000 + 7 * 100 000 + 3 * 10 000 + 4 * 1000 + 2 * 100 + 1 * 10 + 2
   656 734 212 = 600 000 000 + 50 000 000 + 6 000 000 + 700 000 + 30 000 + 4 000 + 200 + 10 + 2.

Так вы сможете разложить на разрядные слагаемые любое, даже самое гигантское, число. Важно разобраться в разрядах и классах чисел, тогда вы точно ничего не перепутаете.

Источник