Как найти сумму аналитическим способом

Глава 2. Решение задач

Рассчитайте, какую сумму необходимо положить на депозит, чтобы через пять лет она выросла до 500 000 руб., если ставка процента – 15% годовых и проценты начисляются ежеквартально. Ответ округлите до копеек. А если первоначально положить 250 000 руб., то какую сумму следует ожидать через пять лет? Ответ округлите до копеек.

Алгоритм решения задачи

При решении задачи аналитическим способом используем формулу:

,где

ПС – текущая стоимость вклада

БС – будущая стоимость вклада

Кпер – общее число периодов начисления процентов

Ставка – процентная ставка за период

Данная формула не учитывает знак «минус» для денежных потоков от клиента. Подставив в формулу числовые данные, получим:

Для расчета суммы текущего вклада зададим исходные данные в виде таблицы.

Поскольку необходимо рассчитать текущую сумму вклада на основе постоянной процентной ставки, то используем ПС(ставка ;кпер;плт;бс;тип). Опишем способы задания аргументов данной функции.

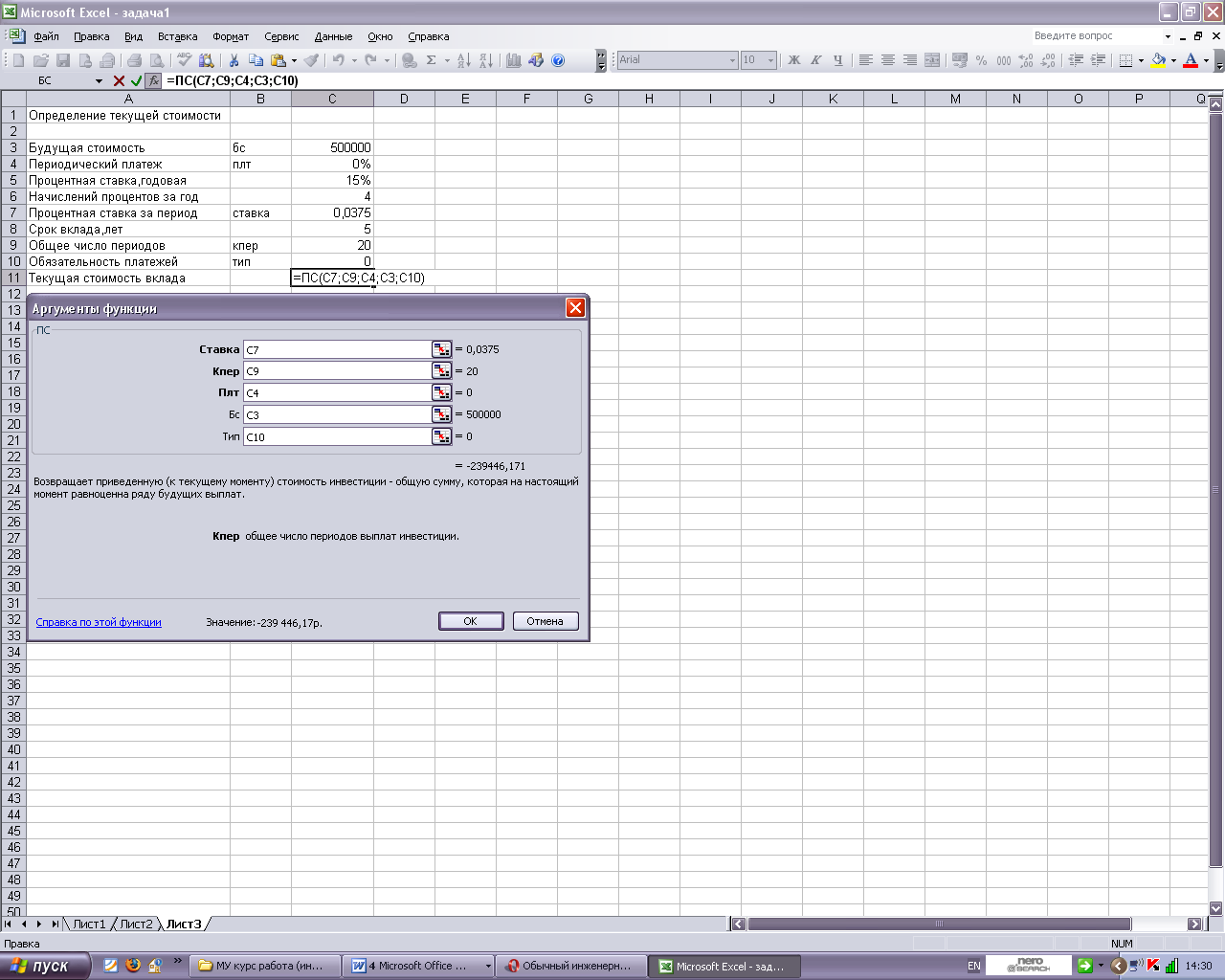
В связи с тем, что проценты начисляются каждый квартал, аргумент ставка равен 15%/4. общее число периодов начисления равно 5*4 (аргумент кпер). Аргумент плт отсутствует, так как вклад не пополняется. Аргумент тип равен 0, так как в подобных операциях проценты начисляются в конце каждого периода (задается по умолчанию). Если решать данную задачу с точки зрения вкладчика, то аргумент пс (начальная стоимость) збудет равен отрицательному числу, поскольку для вкладчика это отток его денежных средств (вложение средств). На рисунке 1 показан ввод заданных параметров.

Рисунок 1 — Фрагмент листа Excel с решением задачи об определении текущей стоимости

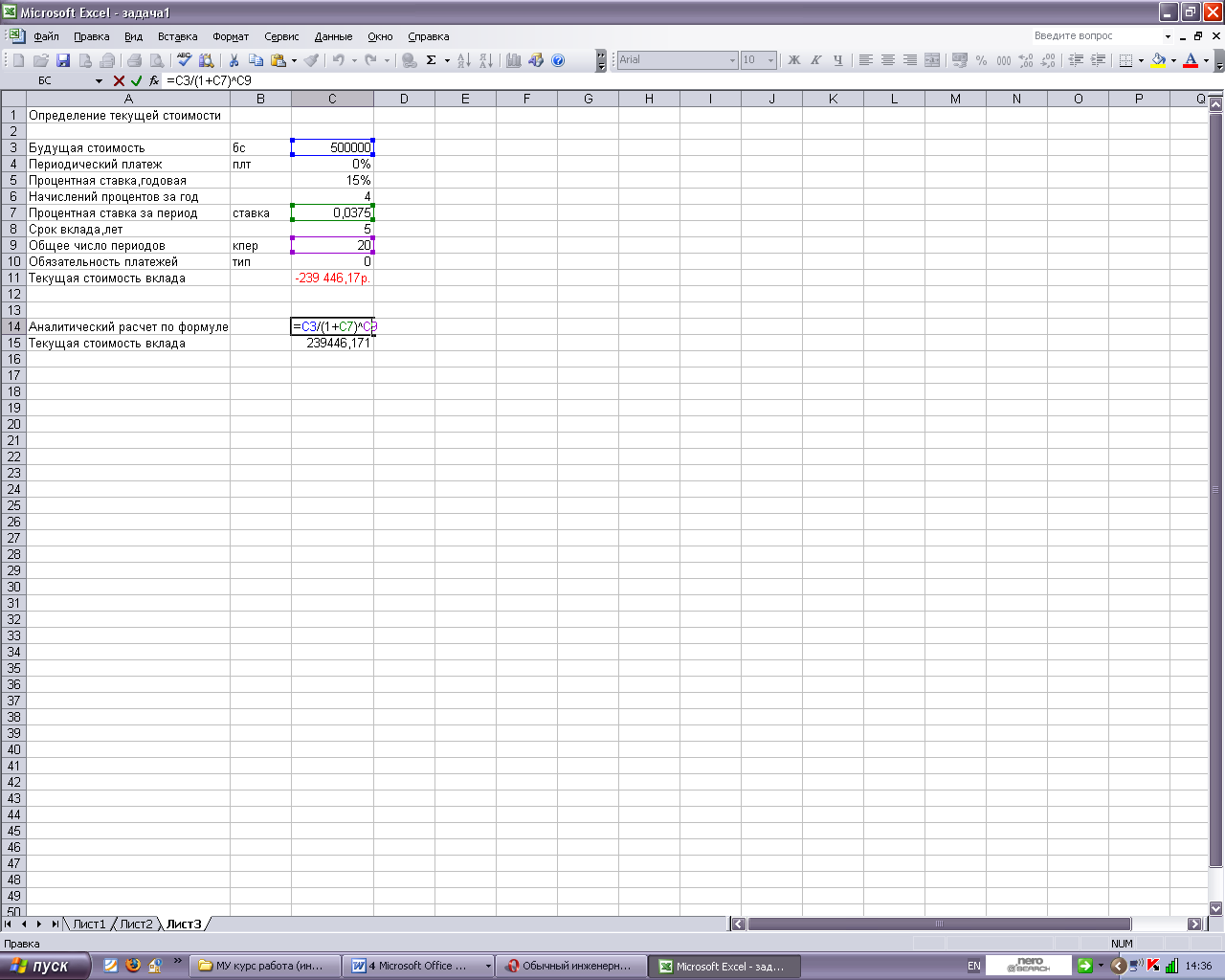
Проверка решения аналитическим методом представлена на рисунке 2.

Рисунок 2 — Фрагмент листа Excel с аналитическим решением задачи об определении текущей стоимости

Далее решаем вторую часть задачи.

Аналитический способ решения:

Подставив в формулу числовые значения, получаем:

БС = 250000 – (1+ 0,0375) 20 = 522037,999 руб.

Поскольку необходимо рассчитать единую сумму вклада на основе постоянной процентной ставки, то используем БС(ставка;кпер;плт;пс;тип).

Если решать данную задачу с точки зрения вкладчика, то аргумент пс (начальная стоимость вклада), равный 250 000 руб., задается в виде отрицательной величины (-250 000), поскольку для вкладчика это отток его денежных средств (вложение средств). На рисунке 3 показано решение второй части задачи.

Рисунок 3 — Фрагмент листа Excel с решением задачи об определении будущей стоимости

Проверка решения аналитическим методом представлена на рисунке 2.

Рисунок 4 — Фрагмент листа Excel с аналитическим решением задачи об определении будущей стоимости

Определите, через сколько лет обычные ежеквартальные платежи размером 3 150 руб. принесут доход в 450 000 руб. при ставке 14% годовых. Рассчитайте сумму ежеквартальных платежей, исходя из десятилетнего срока. Ответ округлите до копеек.

Алгоритм решения задачи

Решим первую часть задачи.

Аналитический способ решения задачи.

У нас есть формула:

Поскольку в данной задаче ПС = 0, выразим из данной формулы КПЕР:

Найдем количество лет, через которые данные платежи принесут заданный доход. Для этого 52/4 = 13 лет.

Решим задачу в MS Excel.

Для нахождения количества лет, через которые платежи размером 3150 рублей принесут доход в 450000 рублей, для начала найдемобщее количество периодов выплаты на основе периодических постоянных выплат и постоянной процентной ставки: КПЕР (ставка ;плт;пс;бс;тип), а затем общее число периодов выплат разделим на количество начислений процентов за год. Таким образом, мы ответим на вопрос задачи.

В данном случае ставка = 14%/4, тип = 0 (по умолчанию), пс отсутствует, плт по условию задачи = -3150 руб, т.к. данная сумма для вкладчика является оттоком средств.

На рисунке 5 мы видим нахождение общего количества периодов выплат с помощью MS Excel.

Рисунок 5. Фрагмент листа Excel с нахождение общего количества периодов выплат

На рисунке 6 изображено второе действие задачи (Мы поделили кпер на количество начислений процентов за год).

Рисунок 6. Фрагмент листа Excel с нахождение количества лет

Таким образом, при обычных ежеквартальных платежах размером 3 150 руб. и ставке 14% годовых потребуется 13 лет для получения дохода в 450000 рублей.

Теперь решим вторую часть задачи.

Решение аналитическим способом:

Выплаты, определяемы функцией ПЛТ, включают основные платежи и платежи по процентам. Расчет выполняется по формуле

Для определения ежемесячных выплат применяется функция ПЛТ с аргументами: Ставка = 14%/4 (ставка процента за квартал); Кпер = 10*4 = 40 (общее число кварталов начисления процентов); Бс = 450000 (будущая стоимость вклада); Тип = 0,так как в подобных операциях проценты начисляются в конце каждого периода (задается по умолчанию). Иллюстрация решения данной задачи в Excel приведена на рисунке 5.

Рисунок 5 — Иллюстрация применения функции ПЛТ

Результат со знаком «минус», так как 5322,28 руб. клиент ежеквартально вносит в банк.

Имеется следующая таблица.

Определить сумму налога на наследование при условии, что действует налоговая шкала, представленная в таблице.

В указанной таблице процент взимается со стоимости, превышающей нижнюю границу рассматриваемой ступени налоговой шкалы, а числа задают фиксированную сумму налога МРОТ.

Размер облагаемой налогом суммы МРОТ

Решение аналитическим способом.

Для решения этой задачи нам потребуется рассмотреть каждого наследника.

Первый из них – Лушников является наследником первой очереди и унаследованная им сумма составляет 1560 руб. Исходя из второй таблицы, он облагается налогом, равным 5% от суммы наследования (1560*0,05). Сумма налога = 78 руб.

Федоров – наследник второй очереди и его сумма наследования составляет 3500 руб., следовательно, его сумма налога составляет 3500*0,3+255 = 1275 руб.

Семенов является наследником первой очереди, его сумма наследования равна 2200 руб., а сумма налога, которую он должен выплатить составляет 2200*0,1+42,5 = 262,2 руб.

Бобров – наследник первой очереди, сумма наследования равна 760 руб., сумма налога равна 0 руб.

И наконец, Колесников – наследник второй очереди, он имеет сумму наследования 1800 руб., а сумма налога равна 1800*0,2+85 = 445 руб.

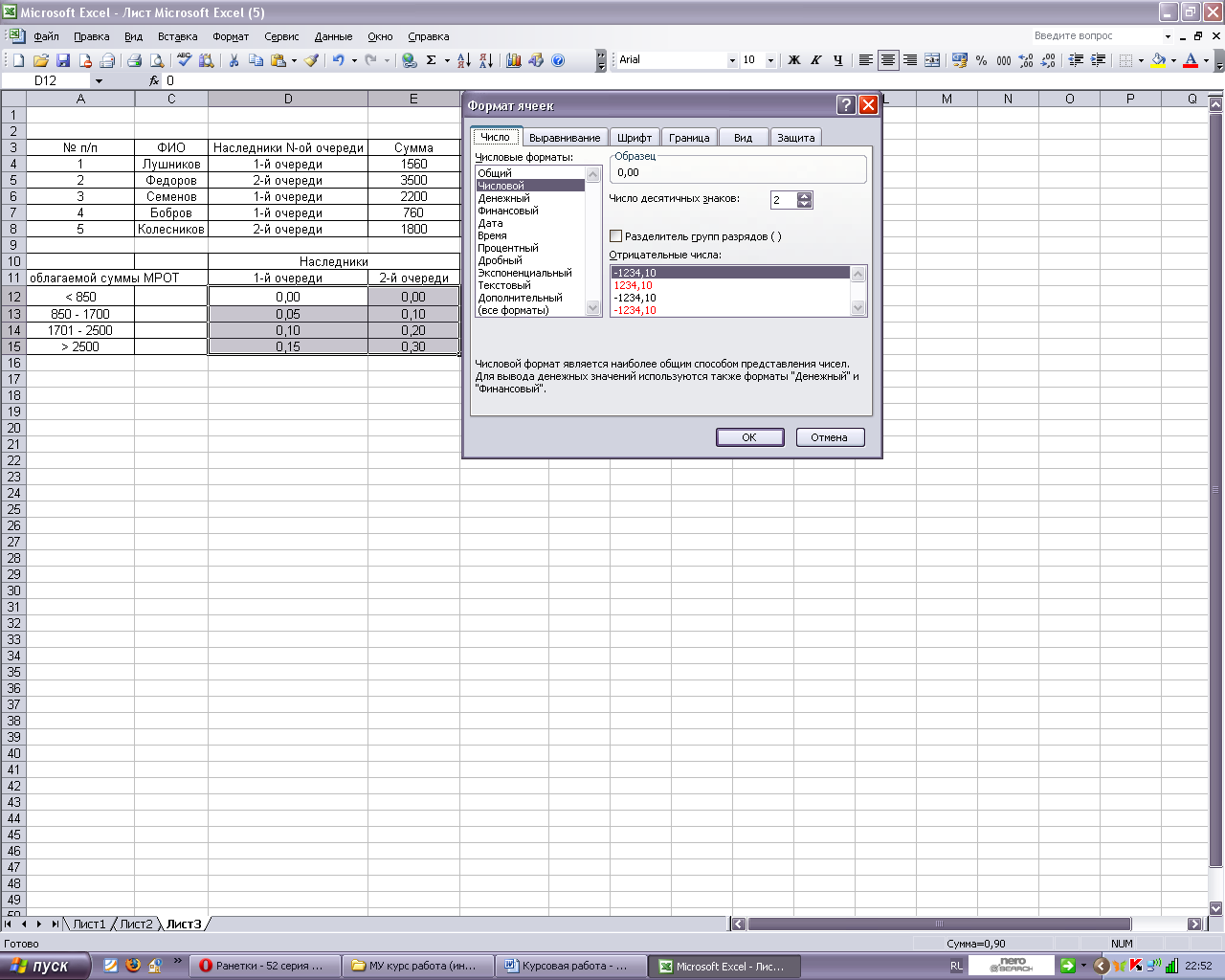
Теперь нам нужно решить эту задачу в MS Excel. Для этого создаем 2 данные таблички, как показано на рисунке 6. При этом во второй табличке изменим формат ячеек (Для этого выделяем 2 и 3 столбцы таблицы, нажимаем правой кнопкой мыши: формат ячеек – числовой, с количеством чисел после запятой = 2). Также при рассмотрении 2 таблицы мы не будем учитывать числа 42,2; 85,0; 127,5 и 225,0 из 2 и 3 столбца для более удобных расчетов. Данные числа мы приплюсуем в конце. Данные преобразования показаны на рисунке 7.

Рисунок 6. Фрагмент листа Excel с условиями задачи 3.

Рисунок 7. Фрагмент листа Excel с установлением формата ячеек.

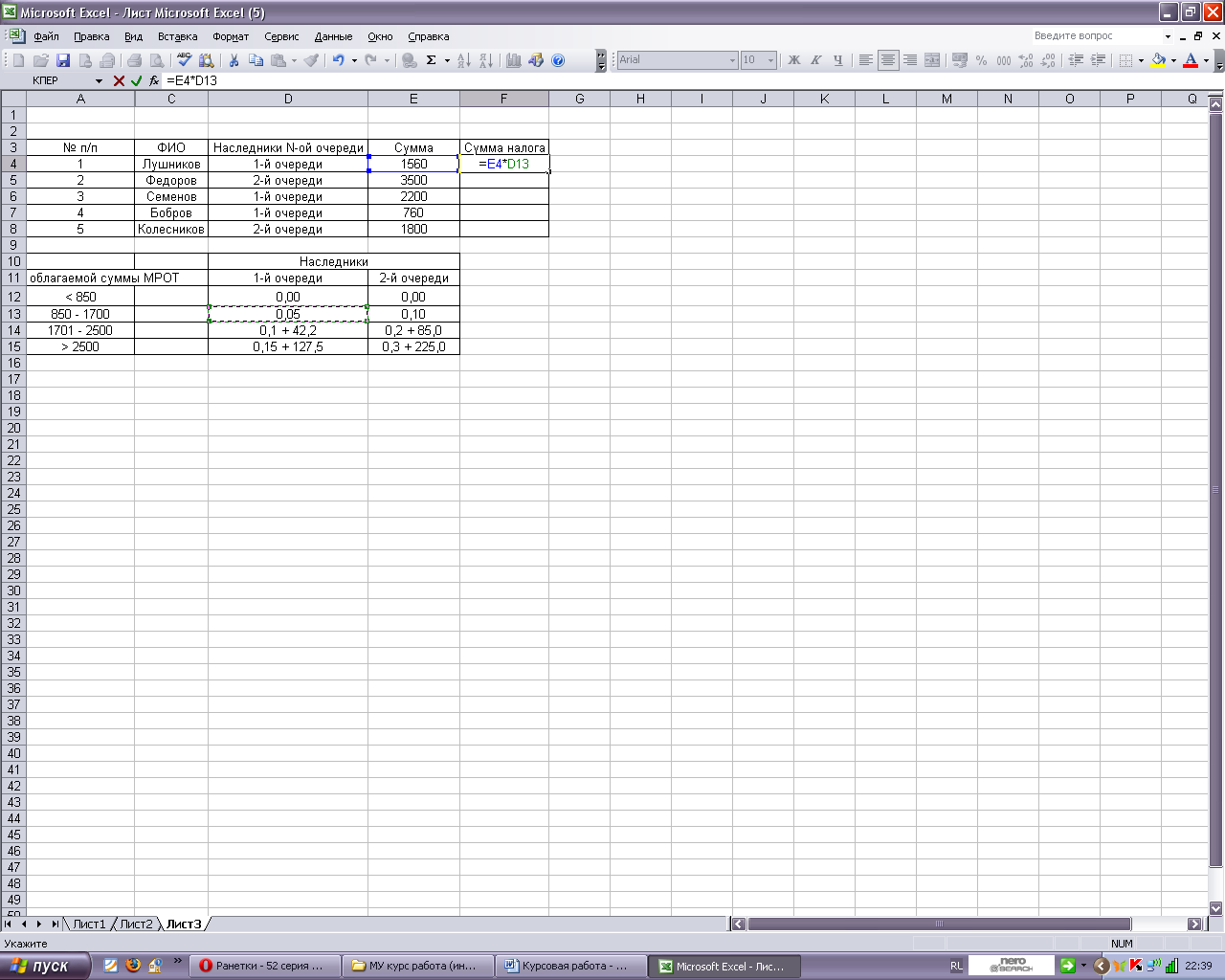
На рисунке 8 показано первое действие задачи.

Рисунок 8. Фрагмент листа Excel с началом решения задачи

Аналогичным способом находим остальные суммы налога. Результаты вычисления показаны на рисунке 9.

Рисунок 9. Фрагмент листа Excel с решением задачи

И в последнем действии мы находим окончательную сумму налога для каждого наследника. На рисунке 10 показано, как найти сумму налога в конечном счете. Ответы, полученные в результате вычисления, показаны на рисунке 11.

Рисунок 10. Фрагмент листа Excel с выполнением действий

Рисунок 11. Фрагмент листа Excel с результатом выполненных действий

Как мы видим, Excel – это не более изощренный текстовый редактор с сеткой, которая принуждает пользователя заносить информацию в небольшие отдельные ячейки, вместо того, чтобы предложить все пространство листа.

Огромная разница между ячейками рабочей таблицы и страницами текстового редактора состоит в том, что каждая ячейка позволяет не только редактировать и форматировать текст, но и выполнять вычисления. Эти вычисления основаны на формулах, которые пользователь создает в различных ячейках таблицы, зачастую пользуясь мастером функций, очень облегчающим работу.

Вычислительные возможности Excel и ее способности по редактированию и форматированию дают в итоге чудесную программу для создания любого документа, который может содержать текстовые и числовые данные и позволяет выполнять вычисления.

Поскольку таблицы содержат динамические формулы, их итоговые значения всегда будут актуальны. А это очень важно в современных условиях.

Список используемой литературы

1. Гобарева Я.Л. Технология экономических расчетов средствами MS EXCEL: учебное пособие / Я.Л.Гобарева, О.Ю.Городецкая, А.В.Золотарюк. – М.: КНОРУС, 2006. – 344 с.

2. Информатика и информационные технологии. Учебник для 10-11 классов / Угринович Н.Д. – М.: БИНОМ. – 511 с.

3. Комягин В.Б. Компьютер для студентов. Самоучитель. Быстрый старт. Учебное пособие // М.: Триумф, 2003. с. – 400.

Источник

Сумма ряда

Содержание:

Понятие суммы ряда

Постановка задачи. Найти сумму ряда

где — целые числа.

План решения. Суммой ряда называется предел последовательности его частичных сумм , т.е.

где

1. По условию задачи

Если корни знаменателя различаются на целое число, т.е. где — натуральное число, то члены последовательности частичных сумм ряда легко найти, так как в выражении многие слагаемые взаимно уничтожаются.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

2. Разлагаем общий член ряда на элементарные дроби:

и выписываем несколько членов ряда так, чтобы было видно, какие слагаемые сокращаются при вычислении частичных сумм ряда.

3. Находим -ю частичную сумму ряда:

,

сократив соответствующие слагаемые.

4. Вычисляем сумму ряда по формуле (1)

и записываем ответ.

Пример:

Найти сумму ряда

Решение:

1. Корни знаменателя и различаются на целое число, т.е. Следовательно, члены последовательности частичных сумм ряда легко найти, так как в выражении многие слагаемые взаимно уничтожаются.

2. Разлагаем общий член ряда на элементарные дроби

и выписываем несколько членов ряда:

3. Сокращая все слагаемые, какие возможно, находим -ю частичную сумму ряда:

4. Вычисляем сумму ряда по формуле (1):

Ответ:

Возможно вам будут полезны данные страницы:

Вычисление суммы ряда почленным интегрированием

Постановка задачи. Найти сумму функционального ряда вида

и указать область сходимости ряда к этой сумме.

План решения.

1. Находим область сходимости ряда.

По признаку Коши интервал сходимости определяется неравенством

Если , ряд расходится. Если , ряд сходится условно (по признаку Лейбница). Следовательно, область сходимости определяется неравенствами

2. Делаем в исходном ряде замену , получим степенной ряд

с областью сходимости .

3. Известна формула для вычисления суммы членов бесконечно убывающей геометрической прогрессии

4. Кроме того, имеем очевидное равенство

5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке , целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем

Заметим, что так как ряд (1) сходится в граничной точке , то сумма ряда непрерывна в этой точке (справа). Следовательно,

6. Вычисляем интеграл, делаем замену на и записываем ответ: сумму ряда и область его сходимости.

Замечание. Если ряд имеет вид

то применяем теорему о почленном интегрировании степенного ряда дважды или разлагаем дробь на элементарные:

и вычисляем сумму каждого ряда почленным интегрированием.

Пример:

Найти сумму ряда

и указать область сходимости ряда к этой сумме.

Решение:

1. Находим область сходимости ряда.

По признаку Коши интервал сходимости определяется неравенством

В граничных точках при ряд расходится, при ряд сходится условно.

Следовательно, данный ряд сходится при всех .

2. Сделаем замену Получим геометрический ряд (1) с областью сходимости

3. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии

4. Кроме того, имеем очевидное равенство

5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке , целиком принадлежащем интервалу сходимости, и используя формулу (4), получаем

Заметим, что так как ряд (1) сходится в граничной точке , то его сумма непрерывна в этой точке (справа). Следовательно, формула (5) справедлива при всех .

6. Заменяя на , получаем при

Ответ.

Вычисление суммы ряда почленным дифференцированием

Постановка задачи. Найти сумму функционального ряда вида

и указать область сходимости ряда к этой сумме.

1. Находим область сходимости ряда.

По признаку Коши интервал сходимости определяется неравенством

Если , ряд расходится (не выполнено необходимое условие сходимости). Следовательно, область сходимости определяется неравенствами .

2. Делаем в исходном ряде замену и записываем его в виде суммы двух рядов

Следовательно, достаточно найти суммы рядов

и

3. Известна формула для суммы членов бесконечно убывающей геометрической прогрессии

4. Кроме того, имеем очевидное равенство

5. Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя формулу (1), получаем

6. Вычисляем производную и делаем замену на . Записываем ответ: сумму ряда и область его сходимости.

Замечание. Если ряд имеет вид

то вычисляем сумму трех рядов, причем при вычислении суммы ряда

применяем теорему о почленном дифференцировании степенного ряда дважды.

Пример:

Найти сумму ряда

и указать область сходимости ряда к этой сумме.

Решение:

1. Находим область сходимости ряда.

По признаку Коши интервал сходимости определяется неравенством . Отсюда . В граничных точках ряд расходится, так как не выполнено необходимое условие сходимости. Следовательно, ряд сходится в интервале .

2. Делаем в исходном ряде замену и записываем его в виде суммы двух рядов

Следовательно, достаточно найти суммы рядов

3. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии:

Следовательно, при всех .

4. Кроме того, имеем очевидное равенство

5. Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя формулу (2), получаем

Заменяя на , получим

Ответ.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Источник