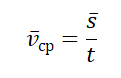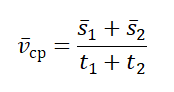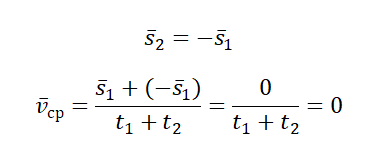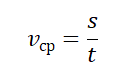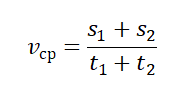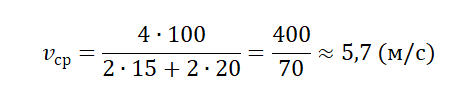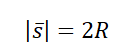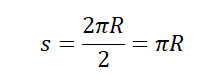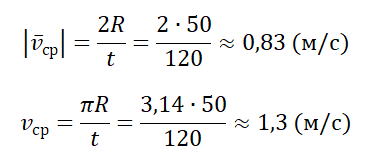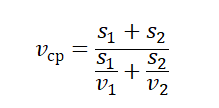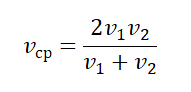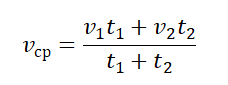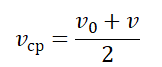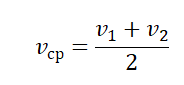Как найти среднюю скорость способы

Способы нахождения средней скорости в физике

Основные понятия и законы кинематики

Кинематика — раздел механики, описывающий механическое движение тел без рассмотрения причин, из-за которых происходит движение.

Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.

Для описания движения нужна система отсчета, относительно которой мы будем описывать движение.

Система отсчета — это система координат, связанная с телом отсчета и прибор для измерения времени.

Тело отсчета — это тело, относительно которого рассматривают положение других тел.

Материальная точка — это тело, размеры которого можно не учитывать при решении задачи.

Траектория — это мысленная линия в пространстве, которую при движении описывает материальная точка.

Траектория движения делится на два типа:

• прямолинейное движение. Это прямой отрезок траектории;
• криволинейное движение. Это кривой отрезок траектории.

Путь — это длина траектории, которую описывает тело или материальная точка за данный промежуток времени.

Перемещение S → — это вектор, соединяющий начальное положение тела или материальной точки с ее конечным положением.

Скорость — это векторная физическая величина, характеризующаяся направлением и быстротой перемещения материальной точки.

В международной системе единиц (СИ) единица измерения скорости обозначается как метр в секунду ( м с ) .

На практике часто используют внесистемную единицу измерения скорости. Например: километр в час ( к м ч ) .

Скорость принято записывать буквой ϑ , в СИ она обозначается как м с .

Как писалось выше, скорость равна отношению пути S ко времени t ( ϑ = S t ) .

Определение средней скорости

Определение: средняя скорость t ( ϑ = S t ) . – это физическая величина, равная отношению вектора всего пройденного пути к затраченному на это движение промежутку времени.

Рассчитать среднюю скорость можно по следующей формуле:

Определение средней путевой скорости

Средняя путевая скорость — это отношение пути или длины траектории, пройденного телом, к интервалу времени, за которое этот путь был пройден.

Формула средней путевой скорости выглядит так:

ϑ с р . п . = ∆ S ∆ t

Примеры решения задач

Автомобиль первый час ехал со скоростью 100 км/ч, после чего сделал остановку. Следующие два часа автомобиль ехал со скоростью 90 км/ч, а затем два часа — со скоростью 80 км/ч. Найдите среднюю скорость на протяжении всего пути автомобиля.

В условии сказано о трех участках пути.

ϑ с р → = S 1 → + S 2 → + S 3 → t 1 + t 2 + t 3

Участки пути мы можем вычислить и посчитать следующим образом:

Первый участок пути составил 1∙100 = 100 километров.

Второй участок пути составил 2∙90 = 180 километров.

Третий участок пути составил 2∙80 = 160 километров.

ϑ с р = 100 + 180 + 160 1 + 2 + 2 = 440 5 = 88 к м ч

Ответ: средняя скорость составляет 88 км/ч.

Автомобиль проехал по дороге расстояние 140 км за время, равное 2 часам, затем сделал остановку. После остановки автомобиль проехал 60 км за 3 часа. Какова средняя скорость автомобиля за весь путь?

ϑ с р → = ∆ S → ∆ t ϑ с р → = S 1 → + S 2 → t 1 + t 2 ϑ с р → = 140 + 60 2 + 3 = 40 к м ч

Ответ: средняя скорость автомобиля составляет 40 км/ч.

Человек занимается бегом и за 2 часа пробежал 5 км, а за следующий час пробежал 3 км. Определите среднюю скорость бегуна.

Искать среднюю скорость будем как во второй задаче.

ϑ с р → = ∆ S → ∆ t ϑ с р → = S 1 → + S 2 → t 1 + t 2 ϑ с р → = 5 + 3 2 + 1 = 2 , 6 к м ч

Источник

Решение задач на среднюю скорость

Решение задач на среднюю скорость

Задачи простые, важно понять и запомнить формулу:

Если участков пути было два, тогда

Если три, то соответственно:

Как вы поняли, смысл таков: в знаменателе складываются отрезки времени, в

числители суммируем расстояния пройденные за соответствующие им отрезки

№1: Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 61

км/ч, а вторую половину времени – со скоростью 87 км/ч. Найдите среднюю

скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Чтобы найти среднюю скорость нужно весь путь разделить на всё время движения.

В задаче сказано о двух участках пути.

Среднюю скорость будем искать по формуле:

Пусть на весь путь автомобиль затратил t часов.

Значит за первую половину времени со скоростью 61 км/ч автомобиль прошёл

0,5∙t∙61 километров, а за вторую половину времени 0,5∙t∙87 километров, тогда:

№2: Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74

км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите среднюю

скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

№3: Путешественник переплыл море на яхте со средней скоростью 17 км/ч.

Обратно он летел на спортивном самолете со скоростью 323 км/ч. Найдите

среднюю скорость путешественника на протяжении всего пути. Ответ дайте в

Мы не знаем, каким было расстояние, которое преодолел путешественник. Знаем

только, что это расстояние было одинаковым на пути туда и обратно.

Когда расстояние не указано его принимают за 1 (в данном случае — одно море).

Тогда время, которое путешественник плыл на яхте, равно 1/17, а время, затраченное

на полет, равно 1/323.

Общее время равно:

Тогда средняя скорость равна:

Путешественник переплыл море на яхте со средней скоростью 20 км/ч. Обратно он

летел на спортивном самолете со скоростью 480 км/ч. Найдите среднюю скорость

путешественника на протяжении всего пути. Ответ дайте в км/ч.

№5: Первую треть трассы автомобиль ехал со скоростью 90 км/ч, вторую треть –

со скоростью 60 км/ч, а последнюю – со скоростью 45 км/ч. Найдите среднюю

скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Чтобы найти среднюю скорость нужно весь путь разделить на всё время движения. В

задаче сказано о трёх участках пути.

Среднюю скорость будем искать по формуле:

Обозначим весь пусть S.

Тогда первую треть пути автомобиль ехал:

Вторую треть пути автомобиль ехал:

Последнюю треть пути автомобиль ехал:

№6: Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть –

со скоростью 120 км/ч, а последнюю – со скоростью 110 км/ч. Найдите среднюю

скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

№7: Первый час автомобиль ехал со скоростью 100 км/ч, следующие два часа – со

скоростью 90 км/ч, а затем два часа – со скоростью 80 км/ч. Найдите среднюю

скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Чтобы найти среднюю скорость нужно весь путь разделить на всё время движения. В

задаче сказано о трёх участках пути.

Среднюю скорость будем искать по формуле:

Исходя из условия мы можем определить протяжённость каждого участка:

Первый участок пути составил 1∙100 = 100 километров.

Второй участок пути составил 2∙90 = 180 километров.

Третий участок пути составил 2∙80 = 160 километров.

№8: Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час – со

скоростью 100 км/ч, а затем два часа – со скоростью 75 км/ч. Найдите среднюю

скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

№9: Первые 120 км автомобиль ехал со скоростью 60 км/ч, следующие 120 км — со

скоростью 80 км/ч, а затем 150 км — со скоростью 100 км/ч. Найдите среднюю

скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Чтобы найти среднюю скорость нужно весь путь разделить на всё время движения. В

задаче сказано о трёх участках пути.

Среднюю скорость будем искать по формуле:

Протяжённость участков дана. Определим время, которое затратил автомобиль на

каждый участок: на первый участок автомобиль затратил 120/60 часов, на второй

участок 120/80 часов, на третий 150/100 часов.

Находим среднюю скорость:

№10: Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со

скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите среднюю

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 807 человек из 76 регионов

Курс профессиональной переподготовки

Физика: теория и методика преподавания в образовательной организации

• Сейчас обучается 358 человек из 68 регионов

Курс повышения квалификации

Современные педтехнологии в деятельности учителя

• Курс добавлен 23.09.2021
• Сейчас обучается 46 человек из 23 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-309466

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Российский совет олимпиад школьников намерен усилить требования к олимпиадам

Время чтения: 2 минуты

Шойгу предложил включить географию в число вступительных экзаменов в вузы

Время чтения: 1 минута

В Минпросвещения предложили организовать телемосты для школьников России и Узбекистана

Время чтения: 1 минута

В МГУ разрабатывают школьные учебники с дополненной реальностью

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Неравномерное движение и средняя скорость

теория по физике 🧲 кинематика

Неравномерное движение — движение с переменной скоростью, которая может менять как направление, так и модуль.

Неравномерное движение можно охарактеризовать средней скоростью. Различают среднюю векторную и среднюю скалярную скорости.

Средняя векторная скорость

Средняя векторная скорость — это скорость, равная отношению перемещения тела ко времени, в течение которого это перемещение было совершено.

v _ср — средняя векторная скорость, s — перемещение тела, совершенное за время t

Направление вектора средней скорости всегда совпадает с направлением вектора перемещения.

Чтобы вычислить среднюю векторную скорость, нужно поделить сумму всех перемещений на сумму всех временных промежутков, в течение которых эти перемещения были совершены:

Пример №1. Миша пробежал стометровку за 16 секунд. Через 1 минуту он вернулся на старт. Найти среднюю векторную скорость мальчика.

Миша совершил одинаковые по модулю, но разные по направлению перемещения. При сложении этих векторов получается 0. Поэтому средняя векторная скорость также равна нулю:

Средняя скалярная скорость

Средняя скалярная (путевая) скорость — это скорость, равная отношению пути, пройденного телом, ко времени, в течение которого этот путь был пройден.

v_ср — средняя путевая скорость, s — путь, пройденный телом за время t

Чтобы вычислить среднюю путевую скорость, нужно поделить сумму всех путей на сумму всех временных промежутков, в течение которых эти пути были преодолены:

Пример №2. Мальчик пробежал по периметру квадратного поля сто стороной 100 м. На первые две стороны мальчик потратил по 15 секунд, а на последние две — по 20 секунд. Найти среднюю путевую скорость мальчика.

У квадрата 4 стороны, поэтому путь мальчика составляют 4 дистанции по 100 м каждая. Поэтому средняя путевая скорость равна:

Средняя скалярная скорость всегда больше или равна модулю средней векторной скорости:

• v_ср= v _ср, если путь равен модулю перемещения. Так бывает в случае равномерного прямолинейного движения.
• v_ср>v _ср, если путь больше модуля перемещения. Так бывает в случае неравномерного прямолинейного или любого криволинейного движения.

Пример №3. Рыболов остановился на берегу круглого пруда и увидел на противоположном берегу удобное для рыбалки место. Он к нему шел в течение 2 минут. Вычислите среднюю путевую и среднюю векторную скорости рыболова после того, как он придет на новое место, если радиус пруда равен 50 м.

Две противоположные точки окружности соединяются отрезком, проходящим через его центр — диаметром. Поэтому модуль вектора перемещения равен двум радиусам пруда:

Чтобы дойти до диаметрально противоположной точки окружности, нужно пройти путь, равный половине окружности:

Переведя 2 минуты в СИ, получим 120 с. Модуль средней векторно скорости равен:

• Если известны скорости на первой и второй половине пути (s₁=s₂), средняя скорость равна:

• Если известно время прохождения отдельных участков пути и скорости движения на этих участках, средняя скорость равна:

• Если тело движется прямолинейно и равноускорено, его средняя скорость равна половине суммы начальной и конечной скорости:

• Если известны скорости тела за равные промежутки времени, его средняя скорость равна:

Пример №4. Первые полчаса автомобиль двигался со скоростью 90 км/ч, а потом 1 час он двигался со скоростью 60 км/ч. Найти среднюю скорость автомобиля.

Нам известны скорости на каждом из участков пути и время, в течение которого каждый из этих участков был преодолен. Поэтому:

Источник