Теоретическая часть. Способ рядов – это метод, с помощью которого можно определить размер малых тел
Способ рядов – это метод, с помощью которого можно определить размер малых тел.
Расположите вплотную вдоль линейки n = 20 крупинок зерна. Измерьте длину ряда l и вычислите диаметр d одной крупинки:
d = l / n (см. рис. №1)
рис.№1 
рис. №2
Аналогичным способом можно определить толщину листа книги. Для этого плотно сожмите книгу и измерьте ее толщину l (без учета обложки). Разделив толщину l на число листов в книге n, найдите толщину одного листа d (см. рис. №2).
Также можно определить диаметр нити или можно определить диаметр проволоки в пружине.
Для этого намотайте на карандаш вплотную, например 20 витков нити и измерьте длину навивки l. Дальше аналогично первому и второму случаю.
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)
Источник
Как найти способ рядов
1. Загадки природы и тайны быта
Вот говорят: «Толщиной с человеческий волос». А какова она – толщина волоса? Можно ли её измерить? Или, как говорят физики, оценить, в том случае, если измерения нельзя выполнить с высокой точностью. Или, допустим, можно ли измерить толщину нитки?
2. Другие х – файлы
Возможны и другие задачи. Можно ли обычной линейкой измерить:
а) толщину страницы учебника;
б) диаметр горошины или пшена;
в) толщину тонкой проволоки?
Смотрите об этом презентацию и при затруднениях читайте текст.
Не поискать ли мне тропы иной,
Приёмов новых, сочетаний странных?
«Ну, и причём здесь Шекспир?» — наверное, подумали Вы? Но …
Шекспир справедливо отметил, что когда наши познания и житейский опыт не могут решить наши проблемы, надо искать другие способы решения. Как правило, какой-нибудь метод, да и отыщется!
3. А мне это надо?
А мне это надо? – спросите Вы. Как знать? Допустим, для шитья используются нитки разной толщины. Она указывается номером на катушке. Причём нитки №10 толще, чем нитки №20.
Для изготовления некоторых элементов электрической цепи необходимо знать толщину проволоки. Для печати книг, газет и журналов используется бумага разной толщины.
А ещё надо просто научиться решать практические задачи, чтобы получать хорошие отметки и сдать экзамен по физике.
4. Истина где-то рядом
Прямые измерения размеров малых или тонких тел невозможны по той причине, что измеряемые величины соизмеримы или даже меньше цены деления используемого прибора. Одним из способов измерения размеров малых тел является, так называемый, метод рядов. Этот метод основан на принципе суммирования длин (масс, объёмов) одинаковых элементов, образующих тело в целом.
Высота стопки одинаковых книг равна сумме высот отдельных книг в этой стопке: h = n · h₀
Толщина (высота) одной книги, в этом случае, равна: h₀ = h : n
Где: n – кол-во книг; h₀ — высота одной книги.
Задача 1. Определить диаметр шарика (бусины).
Обозначим диаметр буквой d . Это и будет размером малого тела, то есть его наибольшей шириной.
Сложность этой задачи заключается в размерах тел, которые такого же порядка, как и цена деления линейки. Диаметр шариков составляет несколько миллиметров и цена деления 1 мм. Это значит, что погрешность такого измерения очень большая. В этом случае лучше применить не прямое измерение диаметра шарика, а косвенное, с использованием метода рядов.
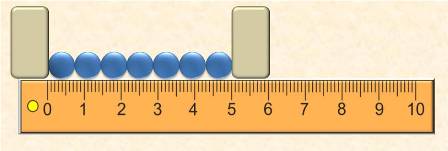
В ряд укладываем несколько шариков. Измеряем длину ряда линейкой и делим её на количество шариков в ряду. Точность косвенных измерений диаметра шарика при таком способе будет значительно выше, чем при прямом измерении линейкой.
Длина ряда: l = 5 см = 50 мм Количество шариков в ряду: n = 7
Диаметр шарика: d = 50 мм: 7 = 7, 1428… мм ≈ 7, 14 мм = 7, 14 · 10 -3 м
Задача 2. Найти диаметр бусины на нитке.
В этом случае задача упрощается. Достаточно плотно сдвинуть некоторое количество бусин на нитке. Расположить этот участок нити вдоль линейки. А затем выполнить прямые и косвенные измерения.
Длина участка нити: l = 6 см = 60 мм Количество бусин: n = 10
Диаметр бусины: d = 60 мм : 10 = 6 мм = 6,0 · 10 -3 м
Задача 3. Определить диаметр тонкой проволоки.
Для решения этой задачи достаточно взять карандаш и намотать на него некоторое количество витков проволоки. Дальнейшие измерения и вычисления аналогичны.
Длина ряда из витков: l = 2 см = 20 мм Количество витков: n = 10
Диаметр (толщина) проволоки: d = 20 мм : 10 = 2 мм = 2 · 10 -3 м
Оформление результатов
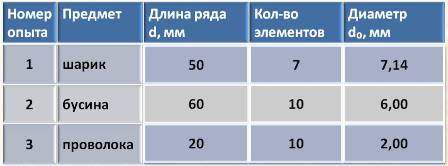
Результаты измерений лучше представлять в виде таблицы. Это удобно для косвенных измерений. А также в случае проведения однотипных измерений для разных тел.
Обычно (если нет особых указаний) практические задачи выполняются с точностью до двух значащих цифр после запятой: 7,1428… мм ≈ 7,14 мм .
Результаты измерений могут быть и такого вида: 6,00 мм. Такой вид записи показывает, что вычисления также выполнены с точностью до сотых. А число либо разделилось без остатка, и дольных значений нет, либо остаток меньшего порядка (тысячные, десятитысячные и т.д.).
Окончательная запись результатов в системе СИ:
d₁ = 7,14 · 10 -3 м; d₂ = 6,00 · 10 -3 м
С учётом погрешности:
d₁ = (7,14 ± 0,07)· 10 -3 м; d₂ = (6,00 ± 0,05) · 10 -3 м.
Погрешность измерений будет уже не 0,5 мм, а в 7 (0,07 мм) и 10 (0,05 мм) раз меньше. И чем больше малых элементов в ряду, тем меньше погрешность измерений.
5. Территория экспериментов
Теперь можно решать практические задачи. В отличие от лабораторных работ, практические задачи не содержат указаний и бланк отчёта необходимо приготовить самому учащемуся. Примеры практических задач:
1. Определить толщину листа учебника физики.
2. Определить толщину нитки в катушке.
3. Определить объём одной капли воды.
Для оформления отчёта одной таблицы мало, надо знать Как составить отчёт по практической работе.
В презентации к уроку есть пример решения задачи и задание для рефлексии.
А если у Вас остались ещё вопросы – спрашивайте на форуме или на странице FQ. Или пишите на электронную почту.
Источник
Суммирование расходящихся рядов методами Абеля, Бореля, Чезаро и Дирихле
Перевод поста Давендра Кападия (Devendra Kapadia) «The ABCD of Divergent Series.»
Выражаю благодарность за помощь в переводе Андрею Дудину.
Какова сумма всех натуральных чисел? Интуиция подсказывает, что ответ — бесконечность. В математическом анализе сумма натуральных чисел является простым примером расходящегося ряда. Тем не менее, математики и физики сочли полезным придать дробные, отрицательные и даже нулевые значения суммам таких рядов. Цель моей статьи — желание отодвинуть завесу тайны, окружающую результаты суммирования расходящихся рядов. В частности, я буду использовать функцию Sum (функция поиска частичных сумм, рядов и т. п. в Mathematica), а так же другие функции в Wolfram Language для того, чтобы объяснить в каком смысле стоит рассматривать следующие утверждения:
Важность обозначений формул буквами A, B, C, и D вскоре станет вам понятна.
Начнем с того, что напомним понятие сходящегося ряда, используя следующую бесконечно убывающую геометрическую прогрессию.
Общий член ряда, начиная с n = 0, определяется по формуле:
Теперь зададим сумму членов ряда от i = 0 до некоторого конечного значения i = n.
Эта конечная сумма называется частичной суммой ряда.
График значений таких частичных сумм показывает, что их значения приближаются к числу 2 с ростом n:
Применяя функцию Limit (поиск предела последовательности или функции в точке) найдем предел значения частичных сумм этого ряда при стремлении n к бесконечности, что подтвердит наши наблюдения.
Функция Sum даёт такой же результат, когда мы производим суммирование членов ряда в пределах от 0 до бесконечности.
Мы говорим, что данный ряд (сумма данной бесконечно убывающей геометрической прогрессии) сходится и что его сумма равна 2.
Вообще, бесконечный ряд сходится, если последовательность его частичных сумм стремится к некоторому значению при неограниченном увеличении номера частичной суммы. В этом случае, предельное значение частичных сумм называется суммой ряда.
Бесконечный ряд который не сходится называется расходящимся. По определению, сумма расходящегося ряда не может быть найдена с помощью рассмотренного выше метода частичных сумм. Тем не менее, математики разработали различные способы присваивания конечных числовых значений суммам этих рядов. Такая сумма называется регуляризованной суммой расходящегося ряда. Процесс вычисления регуляризованных сумм называется регуляризацией.
Теперь мы рассмотрим пример A из вступления.
“A” обозначает Абеля, знаменитого норвежского математика, который предложил одну из техник регуляризации расходящихся рядов. В ходе своей короткой жизни, он умер всего в 26 лет, Абель достиг впечатляющих результатов в решении одних из самых трудных математических задач. В частности, он показал, что решение алгебраического уравнения пятой степени не может быть найдено в радикалах, поставив тем самым точку в проблеме, которая оставалась нерешенной на протяжении 250 лет до него.
Для того чтобы применить метод Абеля, заметим, что общий член данного ряда имеет вид:
Это можно легко проверить, найдя несколько первых значений a[n].
Как можно увидеть на графике ниже, частичные суммы ряда принимают значения, равные 1 или 0 в зависимости от того, четное n или нечетное.
Естественно, что функция Sum выдает сообщение, о том что ряд расходится.
Регуляризация Абеля может быть применена к этому ряду в два шага. Сначала мы строим соответствующий степенной ряд.
Затем мы берем предел этой суммы при x стремящемся к 1, заметим при этом, что соответствующий ряд сходится для значений x меньших, но не равных 1.
Эти два шага можно объединить, сформировав, по сути, определение суммы расходящегося ряда по Абелю.
Мы можем получить тот же ответ используя опцию Regularization для функции Sum следующим образом.
Значение 1/2 представляется разумным, так как оно является средней величиной из двух значений, 1 и 0, принимаемых частичной суммой данного ряда. Кроме того, используемый в данном методе предельный переход интуитивно понятен, т. к. при x = 1 степенной ряд совпадает с нашим расходящимся рядом. Однако, Абель был сильно обеспокоен отсутствием строгости, которое было присуще математическому анализу того времени, и выражал свою обеспокоенность об этом:
«Расходящиеся ряды — изобретение дьявола, и это стыдно на них ссылаться при каких бы то ни было доказательствах. С их помощью, можно сделать любой вывод, какой ему будет угоден, и именно поэтому эти ряды производят столько ошибок и столько парадоксов.» (Н. Х. Абель в письме к своему бывшему учителю Берндту Хольмбою, Январь 1826)
Обратимся теперь к примеру B, в котором утверждается, что:
“B” обозначает Бореля, французского математика, который работал в таких областях как теория меры и теория вероятностей. В частности, Борель связан с так называемой “теоремой о бесконечных обезьянах”, которая утверждает, что если абстрактная обезьяна будет случайным образом ударять по клавиатуре пишущей машинки на протяжении бесконечного количества времени, то вероятность того, что она напечатает некоторый конкретный текст, например, полное собрание сочинений Уильяма Шекспира, отлична от нуля.
Для того чтобы применить метод Бореля заметим, что общий член данного ряда имеет вид:
Регуляризация Бореля может быть применена к быстро расходящимся рядам в два шага. На первом шаге мы вычисляем экспоненциальную производящую функцию для последовательности членов данного ряда. Стоящий в знаменателе факториал обеспечивает сходимость данного ряд при всех значениях параметра t.
Затем мы производим преобразование Лапласа нашей экспоненциальной производящей функции и ищем его значение в точке s=1.
Эти шаги можно объединить, в итоге мы получим, по сути, определение суммы расходящегося ряда по Борелю.
Также мы можем использовать специализированные функции Wolfram Language для поиска экспоненциальной производящей функции и преобразования Лапласа:
При этом, ответ можно получить непосредственно с помощью Sum следующим образом.
Определение суммы по Борелю разумно, т. к. оно даёт тот же самый результат, что и обычный метод частичных сумм, если его применить к сходящемуся ряду. В этом случае можно поменять местами суммирование и интегрирование, и затем определить Гамма-функцию, при этом мы получим, что соответствующий интеграл будет равен 1 и останется просто, по сути, исходная сумма ряда:
Однако в случае с расходящимися рядами поменять местами знаки суммы и интеграла нельзя, что приводит к интересным результатам, которые даёт данный метод регуляризации.
Суммирование по Борелю представляет собой универсальный метод суммирования расходящихся рядов, который применяется, скажем, в квантовой теории поля. О применении суммирования по Борелю существует огромная коллекция литературы.
Пример C утверждает что:
“C” обозначает Чезаро (на англ. языке его фамилия пишется как Cesaro), итальянского математика, который внес значительный вклад в дифференциальную геометрию, теорию чисел и математическую физику. Чезаро был очень продуктивным математиком и написал около 80 работ в период с 1884 по 1886 г., до того, как получил степень PhD в 1887!
Для начала заметим, что общий член ряда, начиная с n = 0, имеет вид:
График показывает сильную осцилляцию частичных сумм данного ряда.
Метод Чезаро использует последовательность средних арифметических значений частичных сумм ряда для того, чтобы подавить осцилляции, что демонстрирует следующий график.
Формально говоря, суммирование по Чезаро определяется как предел последовательности средних арифметических значений частичных сумм ряда. Вычисляя данный предел для ряда из примера C, мы получим ожидаемый нами результат -1/2 (см. график выше).
Сумма по Чезаро может быть получена непосредственно, если мы в функции Sum используем данный тип регуляризации, указав соответствующее значение опции Regularization.
Метод суммирования по Чезаро играет важную роль в теории рядов Фурье, в которых ряды на основе тригонометрических функций используются для представления периодических функций. Ряд Фурье для непрерывной функции может и не сходится, но соответствующая сумма по Чезаро (или чезаровское среднее, как её обычно называют) всегда будет сходиться к функции. Этот красивый результат называется теоремой Фейера.
Наш последний пример утверждает, что сумма натурального ряда равна -1/12.
“D” означает Дирихле, немецкого математика, который совершил огромный вклад в теорию чисел и ряд других областей математики. О широте вкладов Дирихле можно судить, просто введя в Mathematica 10 следующий код.
Регуляризация по Дирихле получила свое название от понятия “ряд Дирихле”, который определяется следующим образом:
Специальным случаем данного ряда является дзета-функция Римана, которую можно определить так:
Функция SumConvergence говорит нам, что этот ряд сходится в том случае, если действительная часть параметра s будет больше 1.
Однако, сама по себе дзета-функция Римана может быть определена и для других значений параметра s с помощью процесса аналитического продолжения, известного из теории функций комплексного переменного. Например, при s = -1, мы получим:
Но при s = -1, ряд, задающий дзета-функцию Римана и есть натуральный ряд. Отсюда мы и получаем, что:
Еще один способ осознания этого результата заключается в том, чтобы ввести бесконечно малый параметр ε в выражение члена нашего расходящегося ряда, а затем найти разложение полученной функции в ряд Маклорена с помощью функции Series, как показано ниже.
Первое слагаемое в разложении выше стремится к бесконечности при приближении параметра ε к нулю, в то же время третий член и все следующие члены стремятся к нулю. Если отбросить все члены, зависящие от ε, то оставшееся число -1/12 как раз и будет суммой по Дирихле натурального ряда. Таким образом, сумма по Дирихле получается путем отбрасывания бесконечно малых и бесконечно больших членов разложения ряда, построенного описанным нами способом. Это находится в противоречии с тем, что принято отбрасывать лишь бесконечно малые величины в обычном математическом анализе, поэтому результат суммирования расходящихся рядов по Дирихле не столь интуитивно понятен.
Аналогично можно получить безумно странное значение 0 для расходящейся суммы квадратов натуральных чисел.
В этом случае в соответствующем разложении отсутствуют члены, не зависящие от параметра ε, в результате мы получаем 0.
Регуляризация Дирихле тесно связана с процессом дзета регуляризации, который используется в современной теоретической физике. В своей знаменитой работе, выдающийся британский физик Стивен Хокинг применил данный метод к задаче вычисления Фейнмановых интегралов в искривленном пространстве-времени. Статья Хокинга описывает процесс дзета-регуляризации очень системно и она приобрела большую популярность после публикации.
Наши знания о расходящихся рядах основаны на глубочайших теориях, разработанных одними из лучших мыслителей последних нескольких столетий. Тем не менее, я соглашусь со многими читателям, которые как и я, чувствуют некоторое непонимание, когда они видят их в современных физических теориях. Великий Абель, вероятно, был прав, когда назвал данные ряды “изобретением дьявола”. Не исключено, что какой-то будущий Эйнштейн, обладающий умом, свободным от всяческих устоев и авторитетов, отбросит преобладающие научные убеждения и переформулирует фундаментальную физику так, что в ней не не будет места для расходящихся рядов. Но даже если такая теория станет реальностью, расходящиеся ряды все равно будут давать нам богатый источник математических идей, освещая дорогу к более глубокому пониманию нашей Вселенной.
Источник
