Как найти процент два способами

Проценты

Процент это один из интересных и часто применяемых на практике инструментов. Проценты частично или полностью применяются в любой науке, на любой работе и даже в повседневном общении. Человек, хорошо разбирающийся в процентах, создаёт впечатление умного и образованного. В данном уроке мы узнаем, что такое процент и какие действия можно с ним выполнять.

Что такое процент?

В повседневной жизни дроби встречаются наиболее часто. Они даже получили свои названия: половина, треть и четверть соответственно.

Но есть ещё одна дробь, которая тоже встречается часто. Это дробь (одна сотая). Данная дробь получила название процент.

Дробь означает, что нечто разделено на сто частей и от этих ста частей взята одна часть. Значит процентом является одна сотая часть.

Процентом является одна сотая часть

Например, от одного метра составляет 1 см. Один метр разделили на сто частей, и взяли одну часть (вспоминаем, что 1 метр это 100 см). А одна часть из этих ста частей составляет 1 см. Значит один процент от одного метра составляет 1 см.

от одного метра уже составляет 2 сантиметра. В этот раз один метр разделили на сто частей и взяли оттуда не одну, а две части. А две части из ста составляют два сантиметра. Значит два процента от одного метра составляет 2 сантиметра.

Еще пример, от одного рубля составляет одну копейку. Рубль разделили на сто частей, и взяли оттуда одну часть. А одна часть из этих ста частей составляет одну копейку. Значит один процент от одного рубля составляет одну копейку.

Проценты встречались настолько часто, что люди заменили дробь на специальный значок, который выглядит следующим образом:

Эта запись читается как «один процент». Она заменяет собой дробь . Также она заменяет собой десятичную дробь 0,01 потому что если перевести обычную дробь в десятичную дробь, то мы получим 0,01. Стало быть между этими тремя выражениями можно поставить знак равенства:

1% = = 0,01

Два процента в дробном виде будут записаны как , в виде десятичной дроби как 0,02 а с помощью специального значка два процента записывается как 2%.

Как найти процент?

Принцип нахождения процента такой же, как и обычное нахождение дроби от числа. Чтобы найти процент от чего-либо, нужно это чего-либо разделить на 100 частей и полученное число умножить на нужный процент.

Например, найти 2% от 10 см.

Что означает запись 2% ? Запись 2% заменяет собой запись . Если перевести это задание на более понятый язык, то оно будет выглядеть следующим образом:

А как решать подобные задания мы уже знаем. Это обычное нахождение дроби от числа. Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.

Итак, делим число 10 на знаменатель дроби

Получили 0,1. Теперь 0,1 умножаем на числитель дроби

Получили ответ 0,2. Значит 2% от 10 см составляет 0,2 см. А если перевести 0,2 сантиметра в миллиметры, то получим 2 миллиметра:

Значит 2% от 10 см составляют 2 мм.

Пример 2. Найти 50% от 300 рублей.

Чтобы найти 50% от 300 рублей, нужно эти 300 рублей разделить на 100, и полученный результат умножить на 50.

Итак, делим 300 рублей на 100

Теперь полученный результат умножаем на 50

Значит 50% от 300 рублей составляет 150 рублей.

Если на первых порах сложно привыкнуть к записи со значком %, можно заменять эту запись на обычную дробную запись.

Например, те же 50% можно заменить на запись . Тогда задание будет выглядеть так: Найти от 300 рублей, а решать такие задачи для нас пока проще

В принципе, ничего сложного здесь нет. Если возникают сложности, советуем остановиться и заново изучить дроби и как их можно применять.

Пример 3. Швейная фабрика выпустила 1200 костюмов. Из них 32% составляют костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?

Здесь нужно найти 32% от 1200. Найденное число будет ответом к задаче. Воспользуемся правилом нахождения процента. Разделим 1200 на 100 и полученный результат умножим на искомый процент, т.е. на 32

Ответ: 384 костюмов нового фасона выпустила фабрика.

Второй способ нахождения процента

Второй способ нахождения процента намного проще и удобнее. Он заключается в том, что число от которого ищется процент сразу умножит на нужный процент, выраженный в виде десятичной дроби.

Например, решим предыдущую задачу этим способом. Найти 50% от 300 рублей.

Запись 50% заменяет собой запись , а если перевести эти в десятичную дробь, то мы получим 0,5

Теперь для нахождения 50% от 300, достаточно будет умножить число 300 на десятичную дробь 0,5

Кстати, по этому же принципу работает механизм нахождения процента на калькуляторах. Чтобы найти процент с помощью калькулятора, нужно ввести в калькулятор число от которого ищется процент, затем нажать клавишу умножения и ввести искомый процент. Затем нажать клавишу процента %

Нахождения числа по его проценту

Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.

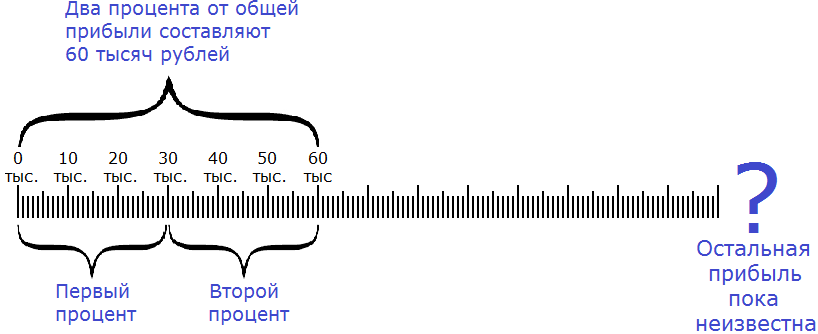
Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:

Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2

60 000 : 2 = 30 000

Мы нашли один процент от общей прибыли, т.е. . Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100

30 000 × 100 = 3 000 000

Мы нашли общую прибыль. Она составляет три миллиона.

Попробуем сформировать правило нахождения числа по его проценту.

Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.

Пример 2. Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.

Читаем первую часть правила:

Чтобы найти число по его проценту, нужно известное число разделить на данный процент

У нас известное число это 35, а данный процент это 7. Разделим 35 на 7

Читаем вторую часть правила:

и полученный результат умножить на 100

У нас полученный результат это число 5. Умножим 5 на 100

500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35

Получили 35. Значит задача была решена правильно.

Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.

Например, предыдущая задача может быть изложена так: число 35 это от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100

В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.

Источник

Задачи на проценты: 3 способа решения с примерами

Как решать задачи на проценты? Есть 3 способа, выбирай тот, который для тебя проще и понятнее.

Умение быстро и правильно решать задачи на проценты важно, как для успешной сдачи ЕГЭ, так и для повседневной жизни. И если в ЕГЭ вы можете встретить такую задачу в задании 11, то в повседневной жизни такие задачи повсюду.

Зарплату повысили на 15%, а потом оштрафовали на 10%, после этого из зарплаты удержали налог 13% — сколько же мы получим в конце месяца? Коммунальные услуги повысили на 15%, сколько они теперь будут стоить? При возврате ж/д билета вернут только 20% стоимости, какую сумму мы получим? Все это задачи на проценты, которые нам приходится решать каждый день.

Поэтому умение быстро и правильно решать задачи на проценты – это полезно.

Задачи на проценты: вся суть

Задачи на проценты, как правило, описывают жизненную ситуацию. В ней присутствует какая-то величина, которая увеличивается или уменьшается на сколько-то процентов. Таким образом, в задаче на проценты упоминается такие данные, как первоначальная величина, конечная величина и процент, на который эта величина изменилась. Чаще всего в задаче требуется найти либо первоначальную величину, либо конечную величину, реже – процент, на который эта величина изменилась.

Решение задач на проценты с помощью формулы простого процента

Формула, которой мы пользуемся при решении задач на проценты, называется формула простого процента:

Х_{конечное} – конечная величина

Х_{первоначальное} – первоначальная величина

k – процент, на который первоначальная величина изменилась

Из этой формулы всегда можно найти первоначальную величину или процент, на который происходит изменение.

Знак стоящий перед k зависит от того, увеличивается первоначальная величина или уменьшается. Так, если величина увеличивается на сколько-то процентов, то ставим знак плюс. Если уменьшается – минус.

Для наглядности приведем несколько простых примеров.

Задача 1

В городе проживало 30 000 человек. В результате строительства нового микрорайона количество жителей увеличилось на 6%. Сколько человек стало проживать в городе?

Решение: Очевидно, что в этой задаче нам известна первоначальная величина – 30 000 человек и процент, на который она увеличилась +6% Нужно найти конечную величину.

30 000 * ((100 + 6)/100) = х

х = 31 800 человек

Ответ: 31 800 человек

Задача 2

Сколько килограмм яблок нужно собрать, чтобы получить из них 5 килограмм сушеных яблок, если известно, что в свежих яблоках содержится 90% воды?

Решение: В этой задаче нам известна конечная величина – 5 килограмм и процент, на который происходит изменение -90%. Нужно найти первоначальную величину:

5 = х * ((100 – 90) / 100)

Задача 3

Холодильник стоимостью 20 000 рублей был продан спустя месяц за 22 000 рублей. На сколько процентов увеличилась стоимость холодильника?

Решение: В данной задаче нам известна первоначальная (20 000 рублей) и конечная величина (22 000 рублей), а найти нужно процент, на который данная величина изменилась.

22 000 = 20 000 * ((100 + х) / 100)

22 000 / 20 000 = 1 + х/100

Решение задач на проценты: метод пропорции

Еще один способ решения задач на проценты – это метод пропорции. Это наиболее простой способ решения таких задач.

Напомним, что пропорция – это равенство двух отношений:

Для нас важно основное свойство пропорции, которое заключается в том, что произведение крайних членов пропорции равно произведению средних членов. Проще запомнить, что мы можем перемножить члены пропорции крест-накрест:

При решении задач на проценты с помощью метода пропорции необходимо руководствоваться следующим правилом:

Далее записываем пропорцию:

Давайте решим приведенные выше примеры задач на проценты с помощью метода пропорции.

Задача 4

В городе проживало 30 000 человек. В результате строительства нового микрорайона количество жителей увеличилось на 6%. Сколько человек стало проживать в городе?

Решение: Итак, в городе проживало 30 000 человек и это всё его население, т.е. 100%. Так и запишем:

Далее население выросло на 6%, т.е. всё его население стало составлять 100% + 6% = 106% и нам неизвестно, сколько это человек, т.е. Х человек. Запишем:

Таким образом, получаем:

Составим пропорцию: Правую дробь пропорции можно сократить на 2, получим: Теперь воспользуемся основным свойством пропорции и перемножим ее члены крест-накрест:

30 000 * 53 = 50х

Далее обе части полученного уравнения мы можем разделить на 50, получим:

Ответ: 31 800 человек

Задача 5

Сколько килограмм яблок нужно собрать, чтобы получить из них 5 килограмм сушеных яблок, если известно, что в свежих яблоках содержится 90% воды?

Решение: Нам неизвестно первоначальное количество всех яблок (всё количество), т.е. это Х, которое составляет 100%. Количество сушеных яблок (часть от первоначального количества яблок) составляет 5 кг. Причем известно, что количество сушеных яблок на 90% меньше от первоначального количества яблок (т.к. 90% — это вода, которая из них испарилась). Следовательно, количество сушеных яблок составит 100% — 90% = 10%. Запишем наши рассуждения:

Запишем наши рассуждения: Сократим правую дробь на 10, получим:Воспользуемся основным свойством пропорции и перемножим ее члены крест-накрест:

Задача 6

Холодильник стоимостью 20 000 рублей был продан спустя месяц за 22 000 рублей. На сколько процентов увеличилась стоимость холодильника?

Решение: Нам известно, что исходная цена – 20 000 рублей, следовательно, 20 000 рублей – это 100%. Тогда конечная цена 22 000 рублей – это неизвестное количество процентов, т.е. Х%. Так и запишем:

Теперь запишем пропорцию: Сократим левую дробь на 2 000, получим: Воспользуемся основным свойством пропорции, то есть перемножим ее члены крест-накрест:

В результате решения мы получили результат 110%, но он не является ответом! Ведь нам нужно найти, на сколько процентов изменилась стоимость холодильника. Чтобы это узнать, нужно из полученного числа процентов отнять 100%:

Решение задач на проценты методом коэффициентов

Можно назвать еще один метод решения задач на проценты, который является следствием из формулы простого процента. Так, формулу простого процента можно переписать следующим образом:

Таким образом, мы получили формулу для решения задач на проценты методом коэффициентов. Полученная формула удобна тем, что при достаточной практике простые задачи на проценты можно решать в уме, даже не задумываясь.

Например, яблоки стоили 150 рублей, затем они подорожали на 20%. Найдите новую стоимость яблок.

Применим полученную формулу и получим:

150 * 1,2 = 180 рублей

То есть мы интуитивно 20% превращаем в 0,2 прибавляем единицу, так как происходит увеличение на данное количество процентов, и умножаем на первоначальную стоимость.

Или другой пример. Зарплата работника составляла 25 000 рублей в месяц, в результате применения штрафа за опоздания зарплата сократилась на 10%. Найти сумму зарплаты, которую получит оштрафованный работник.

25 000 * 0,9 = 22 500 рублей

Опять же мы сразу понимаем, что 10% — это 0,1. Т.к. происходит уменьшение первоначальной величины на это количество процентов, то мы вычитаем из единицы этот процент и получаем 0,9. Затем умножаем полученное значение на первоначальную величину. Готово!

Давайте решим этим методом задачу про зарплату и налоги.

Задача 7

В России налог на доходы физических лиц составляет 13%. Зарплата Марии Ивановны после удержания налога на доходы составила 60 900 рублей. Найти сумму зарплаты Марии Ивановны до удержания налога.

Решение: Итак, 13% — это 0,13. Первоначальная зарплата уменьшилась на этот процент, значит, вычитаем из единицы и получаем 1 – 0,13 = 0,87. Подставляем в формулу:

Ответ: 70 000 рублей

Задача 8

В школе 1000 учеников, из них 20% — ученики начальной школы. Среди учеников средней и старшей школы 30% изучают французский язык. Сколько учеников в школе изучают французский язык, если в начальной школе французский язык не изучают?

Решение: Для начала из общего количества учеников исключим тех, кто французский язык точно не изучает, т.е. учеников начальной школы. Ученики начальной школы – это 20%, т.е. 0,2, мы уменьшаем на этот процент, следовательно, вычитаем из единицы и получаем 1 – 0,2 = 0,8.

Из 800 полученных учеников французский язык изучают только 30%.

Обратите внимание, что здесь идет речь о проценте от числа. Т.е. мы не уменьшаем на 30% (в этом случае мы вычитаем значение процента в долях из единицы) и не увеличиваем на 30% (в этом случае мы прибавляем к значению процента в долях к единице), а берем 30% от заданного числа (в этом случае мы умножаем заданное число на значение процента в долях). Всегда внимательно читайте условия задачи!

В нашем случае нам нужно найти 30% от 800:

Это и есть ответ. 240 учеников изучают французский язык в школе.

Ответ: 240 учеников.

Задача 9

Разберем еще одну задачу на проценты, которая часто встречается на ЕГЭ и в которой легко можно допустить ошибку.

Задача: Зарплата рабочего составляла 30 000 рублей, затем зарплату повысили на 30%, а потом понизили на 30%. Какую зарплату стал получать рабочий?

Решение: быстро прочитав условие задачи, сходу хочется дать ответ – зарплата останется прежней, ее размер не изменился. Но это не так! Давайте разбираться.

Будем решать по формуле простого процента.

Первое событие – зарплату повысили на 30%. Следовательно, первоначальную сумму мы увеличиваем на 30%:Второе событие – зарплату понизили на 30%. Следовательно, нашу увеличенную зарплату мы теперь уменьшаем на 30%:Таким образом, рабочий теперь будет получать зарплату 27 300 рублей.

Данную задачу мы могли бы решить в одно действие, применяя формулу для вычисления сложного процента. Напомним ее:

S = P (1 + i) n , где

S – это конечная сумма;

P – это первоначальная сумма;

i – это процент/100;

n – количество периодов.

Т.к. 30% — это 0,3, то, применяя формулу для вычисления сложного процента к нашей задаче, мы получим:

30 000 * (1 + 0,3) 1 (1 – 0,3) 1 = 27 300 рублей

Результат получился тот же.

Ответ: 27 300 рублей

В этой статье были разобраны достаточно простые примеры задач на проценты, чтобы максимально доступно продемонстрировать методы решения задач на проценты. В профильном ЕГЭ с процентами вы можете столкнуться в задаче с экономическим содержанием по вкладам и кредитам. Такие задачи гораздо сложнее и подробное их решение вы можете посмотреть на нашем сайте.

Итак, надеюсь, что данная статья помогла вам понять, как решать задачи на проценты. Мы увидели, что задачи на проценты можно решать тремя способами – с помощью формулы простого процента, методом пропорции и методом коэффициентов. Выбирайте тот, который вам наиболее понятен, и которым вам решать такие задачи проще.

Источник