- Площадь ромба онлайн
- 1. Площадь ромба через сторону и угол
- 2. Площадь ромба через диагонали
- 3. Площадь ромба через сторону и высоту
- 4. Площадь ромба через угол и противолежащую диагональ
- 5. Площадь ромба через угол и диагональ из данного угла
- 6. Площадь ромба через угол и радиус вписанной в ромб окружности
- 7. Площадь ромба через сторону и радиус вписанной в ромб окружности
- Площадь ромба
- Площадь ромба по стороне и высоте
- Площадь ромба по двум диагоналям
- Площадь ромба по углу и противолежащей диагонали
- Площадь ромба по углу и диагонали проведенной из этого угла
- Площадь ромба по стороне и углу между сторонами
- Площадь ромба по радиусу вписанной окружности и углу между сторонами
- Площадь ромба по радиусу вписанной окружности и стороне
- Таблица с формулами площади ромба
- Определения
- Как рассчитать площадь ромба
- Через сторону и высоту
- Через диагонали
- Через сторону и угол
- Через угол и диагональ из этого угла
- Через угол и противолежащию диагональ
- Через угол и радиус вписанной окружности
- Площади фигур. Площадь ромба.
Площадь ромба онлайн
С помощю этого онлайн калькулятора ромба можно найти площадь ромба по известным элементам. Для нахождения площади ромба введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.
| Открыть онлайн калькулятор |
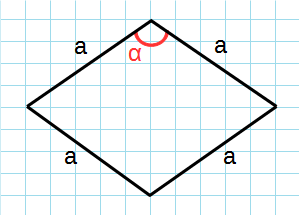
1. Площадь ромба через сторону и угол
Пусть задан ромб ABCD (Рис.1). Выведем формулу вычисления площади ромба через сторону и угол.
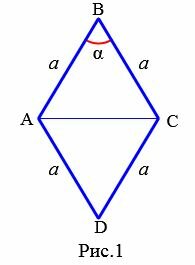 |
Проведем диагональ AC. Тогда ромб делится на два треугольника ABC и ADC. Противолежащие углы ромба равны (свойство 1 статя Ромб). Поэтому треугольники ABC и ADC равны по двум сторонам и углу между ними. Площадь треугольника ABC по двум сторонам и углу между ними вычисляется по формуле:
| \(\small S=AB \cdot BC \cdot \sin \alpha \) |
или, учитывая, что AB=BC=a:
| \(\small S_ |
Аналогично, площадь треугольника ADC вычисляется по формуле
| \(\small S_ |
Поэтому площадь ромба равна:
2. Площадь ромба через диагонали
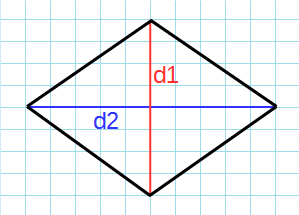
Пусть известны диагонали d1 и d2 ромба ABCD (Рис.2). Выведем формулу вычисления площади ромба через диагонали.
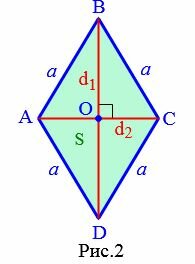 |
Поскольку диагонали ромба перепендикулярны и точкой пересечения делятся пополам (свойства 6 и 5 ромба), то они разделяют ромб на четыре прямоугольных треугольника. Тогда эти прямоугольные треугольники равны по двум катетам: \( \small \frac
| \(\small S_ |
Тогда площадь ромба равна:
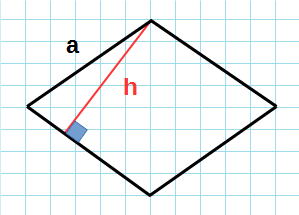
3. Площадь ромба через сторону и высоту
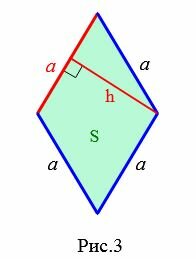 |
Пусть известны сторона a и высота h ромба (Рис.3). Так как ромб является параллелограммом, то площадь ромба вычисляется по формуле площади параллелограмма:
4. Площадь ромба через угол и противолежащую диагональ
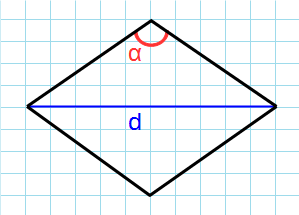
Пусть известны один из углов α=∠ABC ромба и противолежащий диагональ d=AC (Рис.4). Выведем формулу вычисления площади ромба.
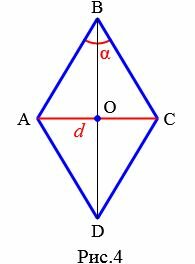 |
Проведем другой диагональ BD. Как было отмечено в параграфе 2, диагонали ромба разделяют его на четыре равных прямоугольных треугольников. Найдем площадь одного из них:
| \(\small S_ | (3) |
| \(\small \frac<\large OB > <\large AO>= \mathrm |
| \(\small OB= AO \cdot \mathrm | (4) |
Подставим (4) в (3):
| \(\small S_ |
или, учитывая что \( \small AO=\frac<\large d><\large 2>,\) получим:
| \(\small S_ | (5) |
Тогда площадь ромба равна:
| \(\small S= 4 \cdot S_ | (6) |
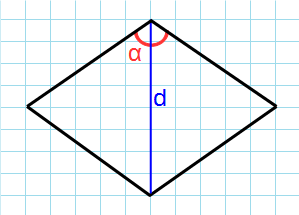
5. Площадь ромба через угол и диагональ из данного угла
Пусть известны один из углов α=∠BAD ромба и диагональ из данного угла d=AC (Рис.5). Выведем формулу вычисления площади ромба.
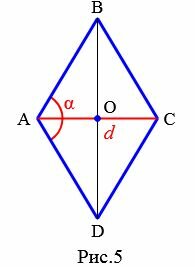 |
Проведем другой диагональ BD. Как было отмечено в параграфе 2, диагонали ромба разделяют его на четыре равных прямоугольных треугольников. Найдем площадь одного из них:
| \(\small S_ | (7) |
| \(\small \frac<\large OB > <\large AO>= \mathrm |
| \(\small OB= AO \cdot \mathrm | (8) |
Подставим (8) в (7):
| \(\small S_ |
или, учитывая что \( \small AO=\frac<\large d><\large 2>,\) получим:
| \(\small S_ | (9) |
Тогда площадь ромба равна:
| \(\small S= 4 \cdot S_ | (10) |
6. Площадь ромба через угол и радиус вписанной в ромб окружности
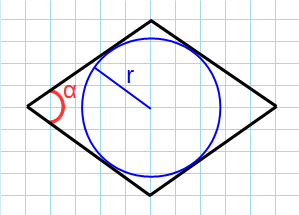
Пусть известны один из углов α=∠ABC ромба и радиус r вписанной в ромб окружности (Рис.6). Выведем формулу вычисления площади ромба.
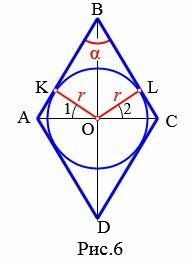 |
Как мы отметили выше, диагонали разделяют ромб на четыре равных прямоугольных треугольника. В частности
Тогда \( \small \angle BAO=\angle BCO=90°-\frac< \large \alpha > <\large 2>\). Треугольники AKO и CLO также прямоугольные. Следовательно
| \( \small \angle 1=90°- \angle BAO \) \( \small =90°- (90°-\frac< \large \alpha ><\large 2>) \) \( \small =\frac< \large \alpha ><\large 2>, \) | (12) |
| \( \small \angle 2=90°- \angle BCO \) \( \small =90°- (90°-\frac< \large \alpha ><\large 2>) \) \( \small =\frac< \large \alpha ><\large 2>. \) | (13) |
Применим теорему синусов для прямоугольного треугольника AOB:
| \( \small \frac<\large AO><\large \sin \frac< \alpha ><2>>= \frac<\large OB><\large \sin \left( 90°-\frac< \alpha > < 2>\right) >\) \( \small =\frac<\large OB><\large \cos \frac< \alpha > < 2>> \) |
Для прямоугольного треугольника AKO имеем:
или, учитывая (12) и KO=r:
Подставляя (15) в (14), получим:
Найдем площадь треугольника AOB:
| \( \small S_ | (17) |
Подставляя (15) и (16) в (17), получим:
| \( \small S_ |
Тогда площадь ромба равна:
7. Площадь ромба через сторону и радиус вписанной в ромб окружности
Пусть известны сторона a=AB ромба и радиус r вписанной в ромб окружности (Рис.7). Найдем площадь ромба.
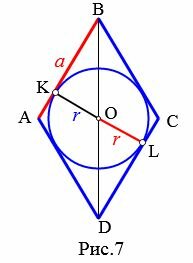 |
Прямая AB является касательной к окружности вписанной в ромб. Тогда \( \small OK ⊥ AB \). Прямая CD является касательной к окружности вписанной в ромб. Тогда \( \small OL ⊥ CD \). Поэтому треугольники BKO и DLO прямоугольные. Эти треугольники равны по гипотенузе и катету (BO=OD, KO=OL). Тогда \( \small \angle BOK=\angle DOL \). Углы BOK и KOD смежные. Следовательно \( \small \angle KOD=180°-\angle BOK. \) \( \small \angle KOD+\angle DOL \) \( \small =180°-\angle BOK+\angle DOL=180°. \) Получили, что отрезки KO и OL находятся на одной прямой. То есть KL=KO+OL=2r. Поскольку \( \small KL ⊥ AB, \) то является высотой ромба. Площадь ромба по стороне и высоте вычисляется из формулы (3). Тогда имеем:
Источник
Площадь ромба
Площадь ромба, формулы и калькулятор для вычисления площади в режиме онлайн.
Для вычисления площади ромба применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор для вычисления площади ромба в режиме онлайн.
Площадь ромба по стороне и высоте
Площадь ромба по двум диагоналям
Площадь ромба по углу и противолежащей диагонали
Площадь ромба по углу и диагонали проведенной из этого угла
Площадь ромба по стороне и углу между сторонами
Площадь ромба по радиусу вписанной окружности и углу между сторонами
Площадь ромба по радиусу вписанной окружности и стороне
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади ромба
В зависимости от известных исходных данных, площадь ромба можно вычислить по различным формулам.
| исходные данные (активная ссылка для перехода к калькулятору) | эскиз | формула |
| 1 | сторона и высота |  |
| 2 | диагонали | 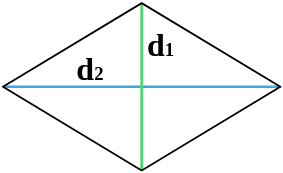 |
| 3 | диагональ и угол между сторонами |  |
| 4 | диагональ и угол между сторонами | 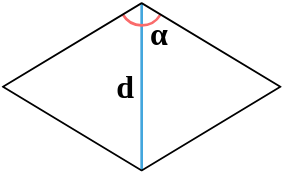 |
| 5 | сторона и угол между сторонами |  |
| 6 | радиус вписанной окружности и угол между сторонами | 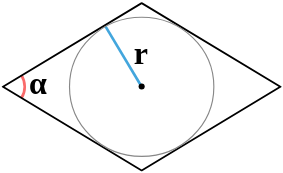 |
| 7 | сторона и радиус вписанной окружности | 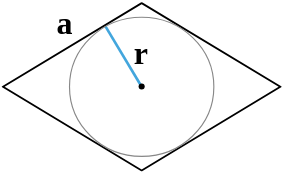 |
Определения
Ромб — это геометрическая фигура, образованная четырьмя последовательно соединенными отрезками (сторонами) одинаковой длины, у которой противоположные стороны попарно параллельны, а угол между любыми двумя смежными сторонами не равен 90 градусов.
Ромб – это частный случай параллелограмма.
Высота ромба – это отрезок проведенный из вершины ромба к противоположной стороне под углом в 90 градусов.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т.д.
Площадь ромба – это численная характеристика, характеризующая размер плоскости, ограниченной четырьмя последовательно соединенными отрезками (сторонами) одинаковой длины, у которой противоположные стороны попарно параллельны, а угол между любыми двумя смежными сторонами не равен 90 градусов.
Источник
Как рассчитать площадь ромба
На данной странице калькулятор поможет рассчитать площадь ромба онлайн. Для расчета задайте длину основания, высоту или длины диагоналей и угол между ними.
Ромб – четырёхугольник, у которого все стороны равны между собой. Ромб является частным случаем параллелограмма. Ромб с прямыми углами называется квадратом.
Через сторону и высоту
Формула для нахождения площади ромба через сторону и высоту:
Через диагонали
Формула для нахождения площади ромба через диагонали:
Через сторону и угол
Формула для нахождения площади ромба через сторону и угол:
Через угол и диагональ из этого угла
Формула для нахождения площади ромба через угол и диагональ выходящая из этого угла:
Через угол и противолежащию диагональ
Формула для нахождения площади ромба через угол и диагональ противолежащая углу:
Через угол и радиус вписанной окружности
Формула для нахождения площади ромба через угол и радиус вписанной окружности:
Источник
Площади фигур. Площадь ромба.
Площадь плоской фигуры — аддитивная числовая характеристика фигуры, полностью принадлежащей
одной плоскости. Если фигуру можно разбить на конечное множество единичных квадратов, то площадь
будет равна числу этих квадратов.
Ромб — это параллелограмм с равными сторонами. Ромб с прямыми углами называется квадратом.
Площадь ромба равна половине произведения его диагоналей.
Воспользуйтесь нашим калькулятором для расчета площади ромба.
Для расчета площади других фигур воспользуйтесь этим калькулятором: площади фигур.
Формулы для вычисления площади ромба.
- Формула площади ромба по длине стороны и его высоте.
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
- Формула площади ромба по длине стороны и углу.
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
- Формула площади ромба по длинам его диагоналей.
Площадь ромба равна половине произведению длин его диагоналей.
где S — Площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба,
α — угол между сторонами ромба,
d1, d2 — длины диагоналей.

Еще некоторые формулы для определения площади ромба:
Источник