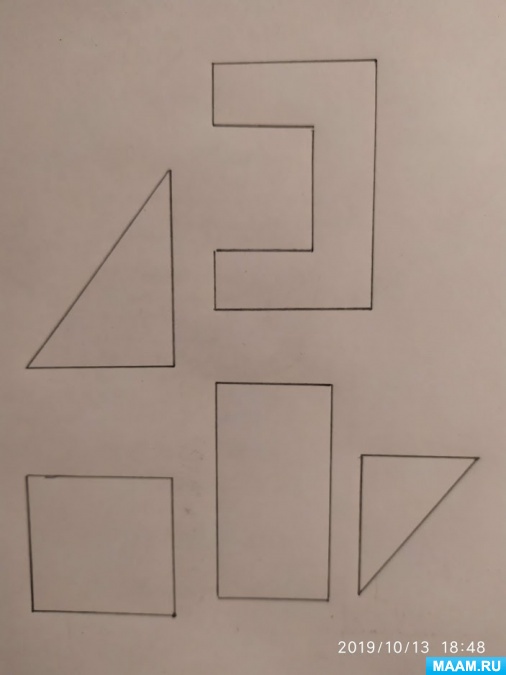Как найти площадь разных фигур разными способами 3 класс

Урок математики «Площадь фигур сложной конфигурации» в 3 классе УМК «Планета знаний»

Инга Мохнаткина
Урок математики «Площадь фигур сложной конфигурации» в 3 классе УМК «Планета знаний»

ЦЕЛЬ. Сформировать умения находить площадь фигур сложной конфигурации.

Задачи. Вспомнить формулы нахождения S прямоугольника, S квадрата, S прямоугольного треугольника, фиксировать затруднения и выявлять причины, формировать умение находить S фигур сложной конфигурации по формуле.

Ход урока

Мотивация к учебной деятельности

Учитель. Ребята, прочитайте девиз сегодняшнего урока.

Девиз: «Где есть желание, найдется путь».

Учитель. Как вы понимаете эти строки? Почему у нас сегодня такой девиз?

Дети. Ищем путь, потерялись, трудности, но при желании можно всегда справиться.

Учитель. Как мы будем строить свою работу?

Ученики. Попытаемся выяснить что мы не знаем.

Самим открыть новый способ, правило.

Актуализация опорных знаний.

Учитель. Начнем свою работу с повторения. Задания, которые нам понадобятся для новых открытий.

1. Увеличьте 37 на 23. (60) О

2. Уменьшите 86 на 34. (52) М

3. Увеличьте 7 в 6 раз. (42) Е

4. Уменьшите 45 в 9 раз. (5) Я

5. Найдите произведение чисел 8 и 4. (32) Т

6. Найдите частное чисел 48 и 6. (8) И

7. Найдите сумму чисел 76 и 18. (94) Г

8. Найдите разность чисел 93 и 25. (68) Е

9. На сколько 68 больше 44? (24) Р

Расположите ответы в порядке убывания.

Учитель. О чем мы с вами будем говорить?

Ученики. О фигурах.

Учитель. Разбейте фигуры на группы. Сколько групп получилось?

Ученики. 1. Прямоугольники.

2. Прямоугольные треугольники.

Учитель. Как можно назвать 3 фигуру? Какая она? Можно её назвать сложной?

Ученики. Фигура сложной конфигурации.

Учитель. Что можно узнать у этой фигуры?

Ученики. Периметр. Площадь.

Учитель. Как будем вычислять площадь?

Постановка учебной задачи.

Учитель. Можно по знакомым формулам вычислить S данной фигуры.

Какая тема будет? Какая цель урока?.

Ученики. Научиться находить S фигуры сложной конфигурации.

Открытие нового знания.

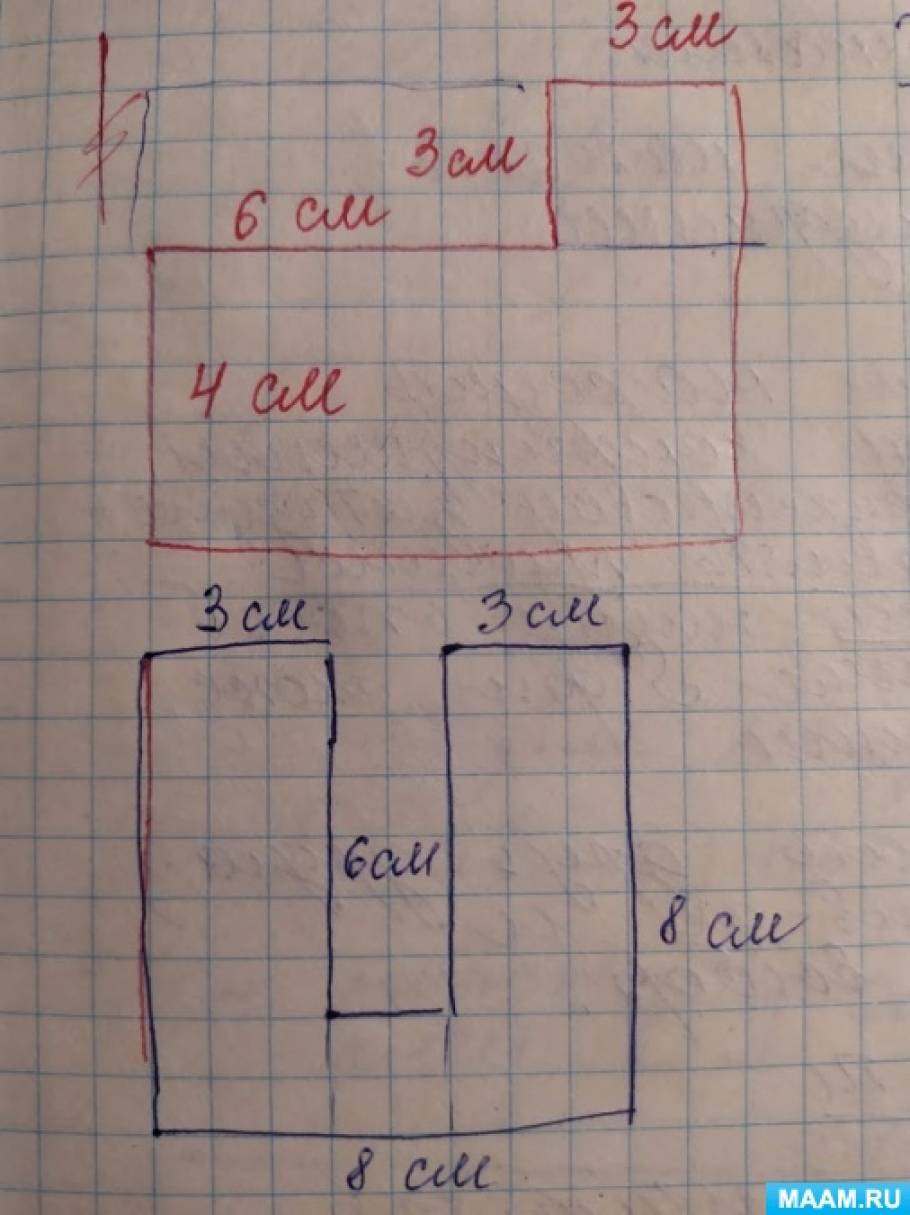
Дети сидят в группах. Каждой группе учитель дает фигуру, ножницы, клей. Дети разными способами пробуют найти площадь фигуры.

Дети определяют 2 способа.

Выступают группы. План действий. Выявление формул

1. Делят фигуру на 3 прямоугольника и складывают их.

2. Дорисовывают фигуру до прямоугольника, из полученной фигуры вычетают дорисованный прямоугольник.

S= S дополненной фиг. — S дополненную часть

Самостоятельная работа с самопроверкой.

Ученики сверяют с эталоном учителя.

Рефлексия.

Учитель. Зачем нужно знать данные формулы?

«Где есть желание, найдется путь»

Были у вас затруднения? Смогли найти путь?

Интегрированный урок английского языка и математики «Время» в 4 классе Класс: 4 «а» инклюзивный Предмет: английский язык и математика Тема урока: Совершенствование речевых навыков учащихся: единицы времени.

Конспект НОД «В гостях у сказки» по теме «Площадь геометрических фигур» Муниципальное дошкольное образовательное учреждение «Центр развития ребенка – детский сад № 6» Энгельсского муниципального района Саратовской.

Конспект урока математики «Переставляем множители» в 3 классе по УМК «Планета знаний» Тема «Переставляем множители» Цель — ознакомление с переместительным законом умножения. Задачи: Предметные: — закрепить название компонентов.

Конспект урока математики в 3 классе «Площадь. Сравнение площадей» Тема урока: Площадь. Сравнение площадей. Вид урока: Открытие новых знаний Технология обучения: технология проблемного обучения Цель урока:.

Открытый урок математики в 1 классе на тему «Дециметр» Тема: «Дециметр» 1 класс Цель. Создать условия для усвоения умений измерять длины предметов в дециметрах и сантиметрах. Задачи. Дать представление.

Открытый урок математики в 4 классе «Встречное движение» Тема урока: Встречное движение. 4 класс Цели урока: • Формировать умение вести поиск и обнаружение способа решения задач на встречное движение.

Урок математики в 1 классе «Сложение и вычитание чисел в пределах 100» МБОУ «Гашунская СОШ им. Очирова А. В.» Тема урока: «Сложение и вычитание чисел в пределах 100» Составила: Босхомджиева Т. К. ,.

Урок математики в 4 классе по теме «Деление на трехзначное число» Тема: Деление на трехзначное число Цель: закрепление умения делить многозначные числа на трехзначное с использованием алгоритма деления.

Урок математики в 1 классе в форме урока-путешествия «Четвертая математическая галактика» по теме «Прибавление числа 4» Урок – путешествие «Четвертая математическая галактика» по теме «Прибавление числа 4» Цель: 1) образовательная – учить выполнять сложение.

Урок русского языка во 2 классе. Обобщение знаний о глаголе Урок русского языка во 2 классе. Тема: Обобщение знаний о глаголе. Тип урока: обобщение знаний Цель урока: — обобщение и систематизация.

Источник

Математика. 3 класс

Конспект урока

Математика, 3 класс

Урок №21. Площадь. Способы сравнения фигур по площади. Единица площади – квадратный сантиметр

Перечень вопросов, рассматриваемых в теме:

— что такое площадь фигуры?

— какие есть способы сравнения фигур по площади?

— что такое квадратный сантиметр?

Глоссарий по теме:

Площадь – внутренняя часть любой плоской геометрической фигуры.

Квадрат – это прямоугольник, у которого все стороны равны.

Основная и дополнительная литература по теме урока:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 56-59.

2. Рудницкая В. Н. Тесты по математике:3 класс. М.:Издательство «Экзамен», 2016 с. 38-43.

3. Волкова Е. В. ВПР. Математика 3 класс Практикум по выполнению типовых заданий. ФГОС. М.: Издательство «Экзамен», 2018, с. 36-53.

Теоретический материал для самостоятельного изучения

Сравним фигуры и расставим их в порядке убывания их площади.

Фигуры расположили в следующем порядке: 4, 2, 1, 6, 5, 3.

В математике говорят: площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией. Когда мы сравниваем площади фигур, мы выясняем, больше или меньше места занимает данная фигура на плоскости. Мы сравнивали эти фигуры способом, который называется «на глаз».

Сравним фигуры и выясним, площадь какой фигуры больше.

Способом сравнения на глаз, определить площадь какой фигуры невозможно.

Для этого существует способ сравнения: наложения.

Вывод: площадь прямоугольника больше площади круга.

Сравним две фигуры.

Изученными способами сравнить площади не получается. Есть еще один способ сравнения: подсчет количества одинаковых мерок.

Посчитаем количество мерок в фигурах: в синей фигуре содержится 6 мерок, в красной-5 мерок, следовательно, площадь синей фигуры больше площади красной, т. к. в синей фигуре 6 мерок-квадратов, а в красной — 5.

В математике мерка- квадрат. А квадрат со стороной 1 см называется квадратный сантиметр и обозначается см 2. .

Задания тренировочного модуля:

1.Выберите правильное высказывание:

Площадь фигуры — это…..

1. сумма длин всех сторон

2. внутренняя часть фигуры

2. внутренняя часть фигуры

2. Выделите фигуры с одинаковой площадью.

Источник

Математика

Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет

С этой картой можно накопить на мечту, жми ⇒

План урока:

Здравствуйте, друзья! Давайте познакомимся. Я — Сова — Мудрая голова.

Масса моего мозга больше, чем у других птиц. Я, как все учителя, терпелива, замечаю все вокруг, слышу шорохи, обдумываю свои шаги. У многих народов меня считают символом знаний.

Сегодня на уроке мы познакомимся с различными способами сравнения и измерения геометрических фигур, а я поделюсь с вами своей мудростью.

Будь внимателен, дружок!

Начинаем наш урок.

Понятие площади фигур

Распределите фигуры на группы.

Какие фигуры вы видите?

Прямые и кривые линии, прямые и кривые, овалы, круг, прямоугольники, квадраты, треугольники.

Чем похожи данные фигуры?

Их можно начертить на плоскости.

Чем они отличаются?

Из бумаги можно вырезать только плоские фигуры, у которых кроме длин сторон, можно вычислить и новую величину — площадь.

Для чего это надо нам знать? Когда может пригодиться?

Величины нужны не только для решения математических задач, но и в жизни. Чтобы сделать поделку, надо определить, какое количество бумаги потребуется. При ремонте квартиры мы считаем, сколько купить рулонов обоев, чтобы оклеить стены комнаты. Величина понадобится при постройке дома, при изготовлении какой-либо продукции в промышленности. Даже в саду и огороде хозяйки считают, хватит ли места на грядке.

Как можно объяснить слово площадь? Значение понятий мы узнаем в толковых словарях.

Прочитайте, какой смысл нового термина в словаре С.И. Ожегова.

Как называется главное место столицы нашей страны?

Красная площадь в Москве.

Общую и полезную площадь имеют разные помещения:

Квартира, в которой вы живете.

Классная комната, где вы учитесь.

Спортивный зал, столовая, бассейн школы.

Разные объекты, занимающие место на земле, можно встретить в любом городе.

Интересно, что некоторые люди заводят дома ушастых сов. Но держать птиц в клетке не рекомендуется: для них требуется более просторная комната, где они могли бы летать.

Жилая площадь квартиры

Любым диким животным лучше жить на воле. Сова – это хищная птица. Она питается грызунами, мышами, полевками, насекомыми и птицами. В этом отношении колоссальная польза от совы состоит в том, что за одно лето она может уничтожить около одной тысячи полевых мышей. Каждый грызун уничтожает более килограмма зерна на посевных площадях страны.

Поле с зерновыми культурами

Понятие площади фигуры:

В математике говорят — площадь фигуры. Это величина пространства, ограниченного замкнутым контуром (периметром фигуры).

Ее можно посчитать математическими методами. С этой целью еще в далекой древности была создана целая наука под названием геометрия. Она применялась для деления поля на земельные участки, но потом ее стали использовать для измерения различных фигур. Поэтому их называют геометрическими фигурами, их место на плоскости — площадью.

Сравнение площадей фигур

Мы можем площади плоских фигур сравнить на глазок. Посмотрите на иллюстрацию.

Картина на стене занимает меньше места, потому говорят, что ее площадь меньше, чем стена. Книги, тетради меньше площади крышки стола. Их как бы наложили сверху, и еще осталось место.

Перечислите способы сравнения фигур по площади.

Можно сравнить на глазок или накладывая предметы, фигуры друг на друга.

Расставьте в порядке уменьшения:

Если получилось так: 3, 1, 2, 4, то вы отлично справились.

Теперь сравните треугольник с кругом:

Круг меньше площади треугольника.

Сравнить можно с помощью любых мерок. На рисунке прямоугольники измеряли заданной меркой — треугольником.

В левый прямоугольник их поместилось 18, а в правый — 20. Делаем вывод, что площадь левой фигуры меньше, чем правой.

Хороший способ сравнения — это подсчет клеток.

Чтобы сравнить площади клетчатых фигур, надо пересчитать количество клеток:

Фигура 3 самая маленькая по площади – 6 клеток. Фигура 2 имеют большую площадь, чем 3. В ней 7 клеток. Площади фигур 1,4,5,6 равновеликие. Они равны 8 клеткам, по площади больше фигур 2 и 3.

Разностное сравнение площадей фигур — это нахождение разницы между большей и меньшей величиной.

Сравните площади фигур 3 и 1. Запишите результаты сравнения.

Проверьте себя:

Ответ: 2 клетки

Квадратный сантиметр, дециметр, метр

Какой меркой лучше измерить площадь фигуры квадрата и прямоугольника?

В 18 веке на Руси вводилась основная мера измерения площади — десятина и четь. Но поля крестьян были неровными, поэтому часто мерками служила урожайная копна. Народ изобретал особые мерки: выть, соха, обжа, коробь, веревка, жеребья. Сейчас мы не используем этих мер.

Начертите прямоугольник со сторонами 5см и 4см. Какими мерками можно измерить фигуру?

Посмотрите на рисунок, утенок измерил прямоугольник с помощью треугольников, ежонок — квадратами, а котенок — прямоугольниками.

Посчитаем, сколько единичных мерок находится в прямоугольнике. У животных получились разные величины: 40, 20, 10.

Всегда ли удобно определять площадь фигуры произвольными мерками?

Вывод: значение величины зависит от выбранной мерки. Чтобы сравнить, нужно договориться об одинаковом способе измерения.

Всегда ли для определения площади фигуры подходит клетка?

Какого размера должна быть клетка?

Я предлагаю измерять как ежик, квадратами по 2 клеточки.

Измерьте длину и ширину этого квадратика. Что получилось?

Длина и ширина равна 1 см.

Единицей измерения площади еще 4-5 тысяч лет тому назад жители древнего города Вавилона считали квадрат, так как именно квадрат имеет превосходные признаки: четыре стороны равны межу собой, четыре прямых угла; можно провести ось и найти центр симметрии. Форма квадрата без изъянов, совершенна, поэтому его легко начертить и плотно покрыть фигуры любой формы.

Если у квадратика сторона 1см – площадь его равна квадратному сантиметру.

1 квадратный сантиметр сравним с ноготком взрослого человека.

Записывается площадь 1 квадратного сантиметра так:

S = 1 кв. см или S = 1 см 2

Латинская буква «эс» обозначает площадь, двойка в правом верхнем углу — две величины: длину и ширину.

Начертите квадрат со стороной 10 сантиметров.

Квадратный дециметр (1 дм 2 ) — это квадрат со стороной 1 дм или 10 см.

Квадратный метр (1 м 2 ) — это квадрат со стороной 1 м или 10 дм. В квадратных метрах обозначается площадь в жилых помещениях, например: в комнатах, коридорах. Эта мерка подойдет для измерения дачного участка, спортивного зала, территории сквера.

А при строительстве школ важно учитывать, сколько квадратных метров должно быть в классе, если для одного ученика по санитарным правилам нужно 4 квадратных метра.

Вы хорошо справляетесь с заданиями. Спине, голове, всему телу нужен отдых. Встаньте на физкультурную минутку.

Физкультминутка

Поднимитесь, вверх потянитесь,

Ниже, ниже тянитесь,

Достаньте мизинцем до пятки.

Получилось? Тогда все в порядке.

Выпрямитесь, грудью вздохните,

Руки шире в стороны разведите.

Соедините в замок на лопатках.

Получилось? Тогда все в порядке.

Глазки зажмурьте, спокойно постойте.

Отдохнули? Теперь посчитайте площадки.

Площадь прямоугольника

Площади простых фигур, таких как квадратов и прямоугольников рассчитывать научились быстро. Для этого измеряют стороны прямоугольника.

Площадь прямоугольника находится по формуле: S = a ∙ b, где длину надо умножить на ширину фигуры.

Задание 1.

Постройте прямоугольник, длина которого 50 мм, а ширина 30 мм.

Можно ли длину и ширину данного прямоугольника выразить в сантиметрах?

Найдите периметр прямоугольника. Р = (a + b) ∙ 2

Р = (5 + 3) ∙ 2 = 16 (см)

Ответ: 16 см

Имеет ли построенная вами фигура площадь?

Да. Прямоугольник имеет длину 5 см и ширину 3 см. Найдем, чему равна площадь прямоугольника по формуле S = a ∙ b.

S = 5 ∙ 3 = 15 см 2

Ответ: площадь прямоугольника равна 15 кв.см.

Задание 2.

Чему равна площадь прямоугольника со сторонами 5 см и 4 см? Рассуждаем так. Нам известна длина и ширина прямоугольника. Площадь равна произведению этих величин.

S = 5 ∙ 4 = 20 см 2

Ответ: 20 кв.см.

Задание 3.

Рассмотрите следующий рисунок:

Как называется данная геометрическая фигура?

Как найти площадь этого многоугольника?

Найти площади отдельных прямоугольников.

Найдите площадь этого многоугольника разными способами.

Первый способ.

Решение.

Измеряем стороны большого прямоугольника.

Длина равна 3 см, а ширина 3 + 1 = 4 (см).

1) 4 · 3 = 12 (см 2 ) – площадь большого прямоугольника.

Длина маленького прямоугольника 3 см, а ширина 1 см. Перемножим эти величины.

2) 3 · 1 = 3 (см 2 ) – площадь маленького прямоугольника.

Теперь из большей фигуры вырезаем два маленьких белых прямоугольника.

3) S = 12 – 3 – 3 = 6 (см 2 ) – площадь многоугольника.

Второй способ.

Решение.

1) 3 · 1 = 3 (см 2 ) – площадь верхнего прямоугольника.

2) 3 · 1 = 3 (см 2 ) – площадь второго прямоугольника.

3) S = 3 + 3 = 6 (см 2 ) – общая площадь многоугольника.

Ответ: S = 6 см 2

Преобразование величин

По формуле S = a ∙ b квадратные сантиметры можно выразить в квадратных метрах. Давайте вспомним, что один метр равен сто сантиметрам.

Мы выполним умножение сторон, и найдем квадратную величину.

Значит: 1 м 2 = 100 ∙ 100 = 10000 см 2

Задание 4.

Вычислите сколько кв.дм в 1 м 2 . Во сколько раз 1 кв. м. больше 1 кв. дм?

Как преобразовать квадратные дециметры в квадратные метры? Давайте рассуждать так. Квадрат со стороной 1 м разделим на 10 столбиков. В каждом таком столбике по 10 кв. дм, то есть всего в кв. м 10 десятков, или 100 дм 2 .

Второй вариант размышлений отталкивается от формулы. Умножаем длину на ширину. 10 дм на 10 дм, получится 100 дм 2 .

1 м 2 = 10 ∙ 10 = 100 дм 2

Ответ: в 1 кв. м содержится 100 кв.дм. 1 кв.м. в сто раз больше одного квадратного дециметра.

Задание 5.

Сколько кв. см в 1 кв. дм? Во сколько раз 1 кв. дм. больше 1 кв. см?

Выражаем квадратные дециметры в квадратных сантиметрах.

1 дм 2 = 10 ∙ 10 = 100 см 2

Ответ: 1 кв.дм равен 100 кв.см. 1 кв.дм в сто раз больше одного квадратного сантиметра.

Выполните упражнение:

Найдите, сколько квадратных дециметров в 8 м 2 , в 25 м 2 , в 45 м 2 9 дм 2

Мы знаем, что 1 м 2 – это 100 дм 2 , то есть число м 2 в 100 раз больше числа дм 2 , поэтому умножим 8 на 100, получим 800 дм 2 .

25 м 2 : умножим 25 на 100 = 2500 дм 2 .

45 м 2 9 дм 2 : это 45 ∙ 100 + 9 = 3100 + 9 = 4509 мм 2 .

Наш урок подходит к концу.

Продолжите фразу:

сегодня я научился

Вы хорошо потрудились, поэтому сможете справиться с самостоятельными заданиями.

Источник