Как найти площадь прямоугольника 3 класс два способа

3 класс. Моро. Учебник №1. Ответы к стр. 87

Дек 17

3 класс. Моро. Учебник №1. Ответы к стр. 87

Числа от 1 до 100
Умножение и деление (продолжение)
Деление нуля на число

Ответы к стр. 87

Учимся решать задачи и выполнять вычисления.

7. Реши уравнения.

75 + x = 90 80 — k = 42 6 • n = 54
x = 90 — 75 k = 80 — 42 n = 54 : 6
x = 15 k = 38 n = 9

8. 1) Найди площадь прямоугольника BCKE и площадь прямоугольника AEKD.

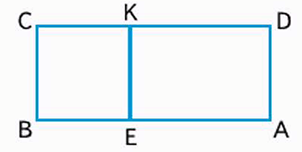
Площадь прямоугольника BCKE: 2 • 2 = 4 (см 2 )
Площадь прямоугольника AEKD: 3 • 2 = 6 (см 2 )

2) Найди двумя способами площадь прямоугольника ABCD.

1 способ:

Нужно сложить площади прямоугольников BCKE и AEKD:
4 + 6 = 10 (см 2 )

2 способ:

Нужно измерить сторонe AB и сторону CD и умножить друг на друга (длину умножить на ширину):
5 • 2 = 10 (см 2 )

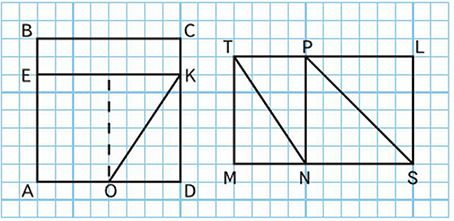
9. 1) Сделай такой же чертёж в тетради и подумай, как можно узнать площадь каждой из фигур с общей стороной OK (рис. 1); с общей стороной NP (рис. 2).

Площадь OKD: 2 • 3 : 2 = 3 (см 2 )
Площадь OKEA: 4 • 3 — 3 = 9 (см 2 )
Площадь OKCBA: 4 • 4 — 3 = 13 (см 2 )

Площадь NPTM: 3 • 2 = 6 (см 2 )
Площадь NPLS: 3 • 3 = 9 (см 2 )
Площадь NPT: 3 • 2 : 2 = 3 (см 2 )
Площадь NPS: 30 мм • 30 мм : 2 = 450 (мм 2 )

2) Узнай, площадь какой фигуры меньше: прямоугольника BCKE или треугольника OKD — и на сколько квадратных сантиметров.

Площадь BCKE: 4 • 1 = 4 (см 2 )
Площадь OKD: 2 • 3 : 2 = 3 (см 2 )

Площадь прямоугольника BCKE больше площади треугольника на: 4 — 3 = 1 (см 2 )

На сколько 9 меньше, чем 72?

На 63: 72 — 9 = 63

Во сколько раз 6 меньше, чем 54?

В 9 раз: 54 : 6 = 9

ЗАДАНИЕ НА ПОЛЯХ:
ЦЕПОЧКА:

54 → 6 → 42 → 100 → 25

Источник

Математика. 3 класс

Конспект урока

Математика, 3 класс

Урок №22. Площадь прямоугольника

Перечень вопросов, рассматриваемых в теме:

1. Как вычислить площадь прямоугольника?
2. В каких единицах измеряется площадь?
3. Какими способами можно сравнить геометрические фигуры?

Глоссарий по теме:

Площадь – внутренняя часть любой плоской геометрической фигуры.

Квадрат – это прямоугольник, у которого все стороны равны.

Прямоугольник – это четырёхугольник, у которого все углы прямые.

Квадратный сантиметр – квадрат со стороной 1 сантиметр.

Основная и дополнительная литература по теме урока:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 60-61.

2. Рудницкая В. Н. Тесты по математике:3 класс. М.: Издательство «Экзамен», 2016 с. 38-43.

3. Волкова Е. В. ВПР. Математика 3 класс Практикум по выполнению типовых заданий. ФГОС .М.: Издательство «Экзамен», 2018, с. 36-53.

Теоретический материал для самостоятельного изучения

Упоминание о первых геометрических фигурах встречается еще у древних египтян и древних шумеров. Учёными-археологами (они ищут разные исторические древности) был найден папирусный свиток (бумага древних египтян, изготавливаемая из растения папирус) с геометрическими задачами, в которых упоминались геометрические фигуры. И каждая из них называлась каким-то определенным словом. Одним определенным словом называлась фигура прямоугольник независимо от того какие стороны были у этого прямоугольника. А если у прямоугольника все стороны были одинаковые, то такой прямоугольник имел специальное название – квадрат. Таким образом, значит, что уже в те далекие времена люди имели представление о геометрии и знали изучаемые этой наукой фигуры. Название «геометрическая фигура» придумали древние греки. И названия всем геометрическим фигурам дали тоже древнегреческие учёные.

Найдём площадь геометрической фигуры.

Чтобы найти площадь фигуры, надо узнать сколько раз в фигуре поместится квадрат со стороной 1 см. Площадь этой геометрической фигуры составляет 18 квадратов. Для удобства подсчёта количество квадратов можно воспользоваться знаниями таблицы умножения. По 6 взять 3 раза получится 18 квадратов.

Найдём площадь прямоугольника со сторонами 6 см и 3 см.

Для этого достаточно умножить длину на ширину. 6 ∙ 3 = 18 см 2

Таким образом, формулируем вывод: чтобы найти площадь прямоугольника, надо длину умножить на ширину.

Источник

Как найти площадь прямоугольника – 9 способов с формулами и примерами

Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.

Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.

По диагонали и стороне

Должна быть известна диагональ и любая из сторон. Действия:

1. Найти квадрат диагонали, то есть умножить ее на саму себя.
2. Найти квадрат известной стороны.
3. Из квадрата диагонали вычесть квадрат стороны.
4. Найти квадратный корень получившейся разности.
5. Умножить его на известную сторону.

Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.

1. Квадрат стороны = 3*3 = 9 см.
2. Квадрат диагонали = 5*5 = 25 см.
3. Вычитаю из квадрата диагонали квадрат стороны: 25-9 = 16 см.
4. Нахожу квадратный корень получившейся разности. Корень из 16 = 4 см.
5. Умножаю корень разности на известную сторону: 16*9 = 144 см.

Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.

По стороне и диаметру описанной окружности

Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.

1. Найдите квадрат диаметра – умножьте диаметр на диаметр.
2. Найдите квадрат известной стороны.
3. Отнимите от квадрата диаметра квадрат стороны.
4. Найдите квадратный корень разности.
5. Умножьте квадратный корень на известную сторону.

Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.

1. Квадрат диаметра: 10*10 = 100 см.
2. Квадрат стороны: 8*8 = 64 см.
3. Отнимаю от квадрата диаметра квадрат стороны: 100-64 = 36 см.
4. Квадратный корень из 36 равен 6 см (потому что 6*6 = 36).
5. Умножаю сторону на корень из разности: 8*6 = 48 см.

Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:

А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.

Диаметр равен двум радиусам, потому что радиус – это половина диаметра.

По радиусу описанной окружности и стороне

Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.

1. Найти квадрат радиуса (умножьте радиус на радиус).
2. Умножить квадрат радиуса на 4.
3. Найти квадрат известной стороны.
4. Отнять от четырех радиусов в квадрате квадрат известной стороны (из второго отнять третье).
5. Найти квадратный корень разности.
6. Умножить корень на известную сторону.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.

1. Квадрат радиуса: 5*5=25 см.
2. Четыре квадрата радиуса: 4*25 = 100 см.
3. Квадрат стороны: 6*6 = 36 см.
4. Отнимаю от четырех радиусов в квадрате квадрат стороны: 100-36 = 64 см.
5. Нахожу квадратный корень разности. Корень из 64 равен 8 см.
6. Умножаю корень на сторону: 8*6 = 48 см.

Радиус = половине диаметра.

Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.

По стороне и периметру – 1 способ

Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).

Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.

Пример. Периметр прямоугольника равен 14 см, а одна из сторон равна 3 см. Найдите площадь.

1. Нахожу вторую сторону прямоугольника:
   1. P=2(a+b).
   2. P=2a+2b.
   3. 14= 2*3+2b.
   4. 14 = 6+2b.
   5. 2b = 14-6 = 8.
   6. b = 8/2.
   7. b = 4.
2. Нахожу площадь по основной формуле. S = 3*4 = 12 см.

По стороне и периметру – 2 способ

1. Умножьте периметр на сторону.
2. Найдите квадрат стороны.
3. Умножьте квадрат стороны на 2.
4. Отнимите от произведения периметра и стороны два квадрата стороны (от первого отнимите третье).
5. Поделите на 2.

Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.

1. Умножаю периметр на сторону: 8*28 = 224 см.
2. Нахожу квадрат стороны: 8*8 = 64 см.
3. Умножаю квадрат стороны на два: 64*2 = 84 см.
4. Отнимаю из первого третье: 224-84 = 140 см.
5. Делю разность на два: 140/2 = 70 см.

По диагонали и углу между диагоналями

Диагонали прямоугольника всегда равны.

1. Найти квадрат диагонали (умножить диагональ на саму себя).
2. Найти половину этого квадрата – умножить его на 0,5.
3. Найти синус угла между диагоналями.
4. Умножить половину квадрата диагонали на синус угла между диагоналями.

Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.

1. Квадрат диагонали: 10*10 = 100 см.
2. Половина этого квадрата: 0,5*100 = 50 см.
3. Синус угла между диагоналями: sin 30 градусов = 0,5.
4. Перемножаю половину квадрата и синус угла, чтобы найти площадь: 50*0,5 = 25 см.

Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).

По радиусу описанной окружности и углу между диагоналями – первый способ

Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.

1. Находим длину диагонали: 6*2 =12 см.
2. Квадрат диагонали равен 144 см.
3. Половина квадрата: 72 см.
4. Синус 30 градусов равен 0,5.
5. Умножаем половину квадрата на синус: 72*0,5 = 36 см.

По радиусу описанной окружности и углу между диагоналями – второй способ

1. Найти квадрат радиуса (умножить радиус на радиус).
2. Умножить квадрат радиуса на два.
3. Найти синус угла между диагоналями.
4. Умножить синус угла на два радиуса в квадрате.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.

1. Квадрат радиуса: 6*6 = 36.
2. Два радиуса в квадрате: 36*2 = 72.
3. Синус 30 градусов равен 0,5.
4. Произведение синуса и двух радиусов в квадрате: 72*0,5 = 36 см.

Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.

Источник

Учебник Моро 3 класс 1 часть. Страница 87

7. Реши уравнения.

8. 1) Найди площадь прямоугольника ВСКЕ и площадь прямоугольника АЕКD.

Измерим линейкой стороны фигур.

ВС=КЕ = 2 см, СК = ВЕ = 2 см. Значит площадь ВСКЕ = 2 • 2 = 4 см².

КD = АЕ = 3 см, ЕК = АD = 2 см. Значит площадь АЕКD = 3 • 2 = 6 см².

2) Найди двумя способами площадь прямоугольника АВСD.

Площадь прямоугольника АВСD можно найти сложив площади ВСКЕ и АЕКD.

Площадь прямоугольника АВСD можно найти перемножив его длину и ширину.

АВ = СD = ВЕ + АЕ = 2 + 3 = 5 см, ВС = АD = 2 см.

9. 1) Сделай такой же чертёж в тетради и подумай, как можно узнать площадь каждой из фигур с общей стороной ОК (рис. 1); с общей стороной NP (рис. 2).

Общая сторона OK есть у трёх фигур: треугольника OKD, четырехугольника OKEA и пятиугольника OKCBF.

Площадь треугольника OKD = (OD • KD) : 2 = (2 см • 3 см) : 2 = 6 см² : 2 = 3 см²

Площадь четырехугольника OKEA = EKDA — OKD = 4 см • 3 см — 3 см² = 12 см² — 3 см² = 9 см²

Площадь пятиугольника OKCBF = ABCD — OKD= 4 см • 4 см — 3 см² = 16 см² — 3 см² = 13 см²

Общая сторона NP есть у четырёх фигур: треугольника NPS, квадрата NPLS, треугольника NPT и прямоугольника NPTM.

Площадь квадрата NPLS = NP • LS = 3 см • 3 см = 9 см²

Площадь треугольника NPS = NPLS : 2 = 9 см² : 2 = 4,5 см² (или можно выразить в миллиметрах — 9 см² = 900 мм², площадь треугольника NPS = 900 мм² : 2 = 450 мм²)

Площадь прямоугольника NPTM = NP • NM = 3 см • 2 см = 6 см²

Площадь треугольника NPT = NPTM : 2 = 6 см² : 2 = 3 см²

2) Узнай, площадь какой фигуры меньше: прямоугольника ВСКЕ или треугольника ОKD — и на сколько квадратных сантиметров.

Площадь прямоугольника BCKE = BC • CK = 4 см • 1 см = 4 см²

Площадь треугольника OKD = (OD • KD) : 2 = (2 см • 3 см) : 2 = 6 см² : 2 = 3 см²

4 см² > 3 см², значит площадь прямоугольника BCKE больше площади треугольника OKD.

4 см² — 3 см² = 1 см². Площадь прямоугольника BCKE больше площади треугольника OKD на 1 см².

На сколько 9 меньше, чем 72?

72 — 9 = 63, значит 9 меньше, чем 72 на 63.

Во сколько раз 6 меньше, чем 54?

54 : 6 = 9, значит 6 меньше, чем 54 в 9 раз.

Источник