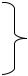Основы геодезии
О геодезии и разный полезный материал для геодезистов.
Аналитический способ
При наличии прямоугольных координат X и Y вершин n -угольника его площадь можно вычислить по формулам аналитической геометрии; выведем одну из таких формул.
Пусть в треугольнике ABC координаты вершин равны X1 , Y1 (A), X2, Y2 (B) и X3, Y3 (C) – рис.6.2.
Из вершин треугольника опустим перпендикуляры на оси координат и обозначим их длину, как показано на рис.6.2.
Площадь треугольника P будет равна сумме площадей двух трапеций I(aABc) и II(bBCc) за вычетом площади трапеции III(aACc)
Выразим площадь каждой трапеции через ее основания и высоту:
Чтобы избавиться от множителя 0.5, будем вычислять удвоенную площадь треугольника. Выполним умножение, приведем подобные члены, вынесем общие множители за скобки и получим:
или в общем виде:
В этой формуле индекс “i” показывает номер вершины треугольника; индекс “i” означает, что нужно брать следующую или предыдущую вершину (при обходе фигуры по часовой стрелке).
Если при группировке членов выносить за скобки Y1, то получится формула:
Вычисления по обоим формулам дают одинаковый результат, поэтому на практике можно пользоваться любой из них.
Хотя формулы (6.11) и (6.12) выведены для треугольника, нетрудно показать, что они пригодны для вычисления площади любого n – угольника.
Оценка точности площади. В большинстве случаев участки на местности имеют форму неправильного n – угольника, причем количество вершин многоугольника n может быть от 30 до 20 и более. Площадь таких участков вычисляют аналитическим способом по прямоугольным координатам вершин, которые, в свою очередь, определяют в результате обработки геодезических измерений. При этом для каждой вершины многоугольника получают координаты и ошибку ее положения относительно исходных пунктов, задающих систему координат на местности.
Выведем формулу для оценки площади многоугольника по известным внутренним углам, длинам его сторон и ошибкам положения mti его вершин.
На рис.6.3 изображен фрагмент многоугольника с вершинами i-1, i, i+1, i+2 и сторонами li-1,li,li+1.
Проведем на вершинах i и i+1 окружности радиусами mti и mt(i+1) и построим биссектрисы углов βi и βi+1. Затем восстановим перпендикуляры к стороне li и найдем проекции отрезков mti и mt(i+1) на эти перпендикуляры:
Построим трапецию, основаниями которой являются отрезки mi и mi+1, а высотой – сторона li и найдем площадь этой трапеции ΔPi. Как известно, площадь трапеции равна произведению полусуммы оснований на высоту, а поскольку основаниями трапеции являются проекции ср.кв. ошибок, то вместо полусуммы нужно взять квадратичную полусумму оснований; таким образом,
Площадь трапеции, построенной на одной стороне многоугольника, является частью ошибки площади всего многоугольника; выполнив квадратичное суммирование площадей ΔPi по всем сторонам, получим:
Из формулы (6.16) можно получить формулу средней квадратической ошибки площади правильного многоугольника с одинаковой ошибкой положения mt всех его вершин:
mP=an * mt * L, (6.17)
где: L – периметр многоугольника,
an – коэффициент, зависящий от n – количества вершин; 
его значения:
n 3 4 5 6 7 8 9 10
an 0.204 0.250 0.256 0.250 0.243 0.231 0.222 0.212
n 11 12 15 20 24 30 60 120
an 0.205 0.197 0.179 0.156 0.143 0.128 0.091 0.065
Формула (6.17) является базовой и при оценке площади неправильных n-угольников, для которых ошибка площади mp оказывается лишь на несколько процентов больше, чем для правильного n – угольника. Так, если площадь неправильного n – угольника при том же периметре в два раза меньше площади правильного n-угольника, то ошибка его площади увеличивается лишь на 20 %.
При неодинаковых ошибках положения вершин многоугольника в формуле (6.17) достаточно вместо mt поставить mt(ср).
Примером применения формулы (6.17) является оценка площади участков, координаты вершин которых получены с топографических планов. Например, для плана масштаба 1:2000 ошибку положения точек можно принять равной mt = 0.50 мм * M = 1 м (при условии, что основа плана достаточно жесткая и ее деформацией можно пренебречь). При площади участка 0.12 га и количестве вершин n=4 (5 или 6) средняя квадратическая ошибка его площади при правильной форме (периметр L = 140 м) будет равна 35 кв.м, а при неправильной форме (периметр L>140 м) она может достигать 40 кв.м.
Другим примером применения формулы (6.17) может служить оценка площади многоугольника, координаты вершин которого получены из полярной засечки, выполненной с одного пункта-станции.
При использовании точных приборов (электронных тахеометров или систем GPS) доля ошибок измерений в ошибке положения точек значительно меньше доли ошибки их фиксации mф на местности. Приняв mti= mф, можно использовать формулу (6.17) для любых способов получения координат вершин многоугольника.
Площадь правильного n-угольника можно выразить через его периметр:
И из формулы (6.17) получить формулу относительной ошибки площади:
для треугольника (n=3) mp/P = 4.24* mt/L,
для четырехугольника (n=4) mp/P = 4.00* mt/L,
для пятиугольника (n=5) mp/P = 3.72 mt/L,
для шестиугольника (n=6) mp/P = 3.46 mt/L.
Таким образом, для приближенной оценки площади 3-4-5-6- угольника в аналитическом способе можно применять формулу:
ошибка этой формулы может достигать 15% – 20% для участков, форма которых заметно отличается от формы правильного n -угольника.
Источник
ЛЕКЦИЯ № 15
Определение площадей. Геометрические, аналитический
и механический способы
В настоящее время площади земельных угодий и инженерных сооружений вычисляют при помощи компьютеров по исходным данным, полученным в результате измерений на местности, по координатам границ объекта, по данным фотографирования местности и др. Но инженер-геодезист должен знать сущность определения площадей объектов традиционными способами, поскольку их геометрия и математическая основа используется в компьютерных программах и нередки случаи, когда приходится определять площади объектов без применения компьютера. К традиционным относятся способы определения площадей: геометрические, аналитические, механические.
15.1. Геометрические способы определения площади
К геометрическим способам определения площади относятся графические (по чертежам местности) и аналитические (расчетные по координатам контура территории).
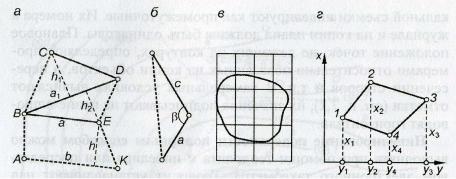
Графические способы определения площади применяются для небольших участков. На местности (рис. 15.1, а ) сложный контур АВСDЕК разделяют на простые геометрические фигуры, вершины которых обозначают вехами. В трапеции АВЕК измеряют основания а и b , высоту h , а в треугольниках ВСD и ВDЕ измеряют основания а 1 и а , высоты h 1 и h . Площадь участка Р = Р 1 + Р 2 + Р 3 , где Р 1 = h ( а
+ b )/2; Р 2 = а 1 h 1 /2; Р 3 = а h 2 /2.
Если треугольнике (рис. 15.1, б ) измерить две стороны и угол β между ними, то
Площадь определяется рассмотренными способами с относительной погреш-
ностью 1 / 1000 – 1/5000.
Рис. 15.1. Геометрические способы определения площадей:
а , б – измерением геометрических фигур; в – с помощью палетки; г – по координатам
Аналогичные способы можно применить для графического определения площади по плану масштаба 1 : М, но с относительной погрешностью 1/50 – 1/1000, зависящей от масштаба и точности плана. С помощью карандаша и линейки контур АВСDЕК (см. рис. 15.1, а ) разграфляют на плане на простые фигуры, а их площади в нашем примере будут вычисляться по формулам, приведенным выше, или по формулам Р 1 = М 2 h ( а + b )/2; Р 2 = М 2 а 1 h 1 /2; Р 3 = М 2 а h 2 /2. Линейные величины а , b и h определяются по плану с погрешностями до 0,5 мм за счет неточностей изображения границ общего контура.
Площадь по плану или карте можно определить при помощи палетки , представляющей прозрачный лист пластика, на который нанесена сетка равных по площади фигур, например квадратов со стороной от 2 до 10 мм (рис. 15.1, в ). Техника определения площади палетками рассмотрена в п. 15.4.
15.2. Аналитический способ определения площад и
Аналитические способы определения площади применяют для замкнутых плоских многоугольников, в которых известны координаты х и у всех вершин (к таким многоугольникам относятся граница населенного пункта, промышленного, сельскохозяйственного или горно-добывающего предприятия, контур лесного массива, озера, болота и т.д.).
Площадь замкнутого многоугольника вычисляют по различным формулам ана-
литической геометрии, наиболее распространены следующие:
2 Р = ∑ х i ( у i +1 – у i -1 );
2 Р = ∑ у i ( х i- 1 – х i +1 ); i = 1, 2, …, n ,
т.е. удвоенная площадь многоугольника равна сумме произведений каждой абсциссы на разность ординат передней и задней по ходу точек, а также сумме произведений каждой ординаты на разность абсцисс задней и передней по ходу точек. Например, для многоугольника 1-2-3-4 (рис. 15.1. г )
2 Р = х 1 ( у 2 – у 4 ) + х 2 ( у 3 – у 1 ) + х 3 ( у 4 – у 2 ) + х 4 ( у 1 – у 3 );
2 Р = у 1 ( х 4 – х 2 ) + у 2 ( х 1 – х 3 ) + у 3 ( х 2 – х 4 ) + у 4 ( х 3 – х 1 );
Площадь вычисляют отдельно по каждой формуле (15.3) с промежуточным контролем разностей координат на условие
∑( у i +1 – у i -1 ) = 0;
∑( х i- 1 – х i +1 ) = 0, i = 1, 2, …, n .
Точность расчетов по формулам (15.4) определяется погрешностями координат. Например, если координаты вершин многоугольника получены теодолитным ходом, то площадь участка получается с относительной погрешностью 1/500 – 1/2000. В случае неверно записанного значения хотя бы одной из координат х i или у i получается ошибочное значение площади при полном совпадении результатов расчетов по формулам (15.3) и (15.4). Такую ошибку можно обнаружить, например, по чрезмерному расхождению между площадью многоугольника и суммой площадей контуров внутри него, нанесенных на план и измеренных планиметром.
15.3. Определение площади полярным планиметром
Полярный планиметр – это механическое устройство для определения площади фигур на планах и картах, а также на других чертежах. На полюсном рычаге 1 планиметра (рис. 15.2) закреплен груз с иглой 3 , представляющей полюс О п планиметра. Вторым концом полюсный рычаг шарнирно входит в гнездо 10 корпуса счетного механизма, установленного на обводном рычаге. Обводный шпиль 6 , укреплен-
ный на обводном рычаге, представляет обводную точку (марку) М (см. рис. 15.4, б ). Рабочий радиус R обводного рычага равен расстоянию АМ между центром шарнира и обводной точкой М (см. рис. 15.4, а ) . Этот радиус можно изменить перемещением корпуса счетного механизма вдоль обводного рычага (рис. 15.3), а величину радиуса отсчитать по шкале на обводном рычаге и верньеру счетного механизма. В нашем примере (см. рис. 15.3) R = 1713.
Рис. 15.2. Полярный планиметр:
полюсный рычаг; 2 –
груз; 3 – игла; 4 – ручка; 5 – опорный штифт;
— обводный шпиль; 7 –
обводный рычаг; 8 –
опора корпуса счетного механизма; 10 –
гнездо соединения рычагов
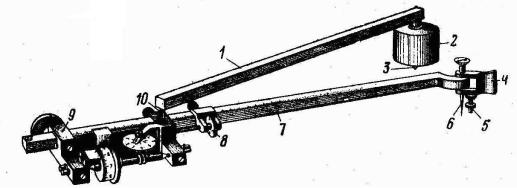
Отсчет по шкалам счетного механизма содержит четыре цифры (см. рис. 15.3). Здесь отсчет u = 3684, где 3 – отсчет по циферблату оборотов счетного колеса; 684
– отсчет по шкале счетного колеса относительно нулевого штриха верньера (68 – номер штриха расположенного ниже нуля верньера; 4 – номер совмещенного штриха верньера).
Рис. 15.3. Счетный механизм планиметра:
1 – указатель; 2 – счетное колесо; 3 – верньер счетного механизма; 4 – винты регулировки зазора между верньером и сетным колесом; 5, 10 – винты регулировки счетного колеса; 6 – опорный ролик; 7 – верньер шкалы радиуса планиметра; 8 – закрепительный винт корпуса счетного механизма; 9 – гнездо соединения рычагов; 11 – циферблат счетчика оборотов счетного колеса
П о в е р к и п л а н и м е т р а
До начала работ планиметр необходимо проверить на комплектность и устранить обнаруженные механические неисправности, затем выполнить следующие поверки устройства:
1. Счетное колесо должно свободно вращаться при незначительном люфте и
с небольшим (0,1 – 0,2 мм) зазором относительно пластинки верньера . При юсти-
ровке вращают два осевых винта 5 и 10 (см. рис. 15.3), в отверстия которых входят конические концы оси счетного колеса.
2. Ось счетного колеса должна быть параллельна прямой, проходящей через обводный шпиль(или метку) и центр шарнира . Для поверки контур обводят шпи-
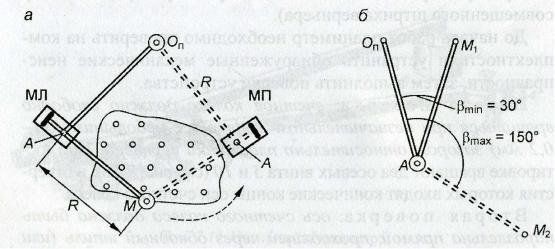
лем (маркой М ) несколько раз в положении планиметра МЛ «счетный механизм слева от фигуры» (см. рис . 15.5, а ) и столько же раз в положении МП «счетный механизм справа от фигуры», не меняя точки полюса О . Если средние разности отсчетов n МЛ и n МП различаются в пределах точности измерений планиметром, то
условие считается выполненным. Для юстировки исправительным винтом изменяют угол между корпусом счетного механизма и обводным рычагом.
Рис. 15.4. Вторая поверка планиметра ( а ); допустимые углы между рычагами ( б )
При работе с неотъюстированным на данное условие планиметром каждую фигуру следует обводить при двух положениях планиметра – ПП и ПЛ и за окончательный результат принимать среднее.
Для измерения площади план кладут на расположенную горизонтально чертежную доску с гладкой поверхностью. Полюс полярного планиметра можно закреплять на плане в положении вне контура или в положении внутри контура , предпочтительное положение полюса – вне контура. Выбирают положение полюса так, чтобы при обводе контура угол β между рычагами (см. рис. 15.4, б ) не был меньше 30 и больше 150°. Обводную точку М совмещают с какой-либо точкой К контура. По счетному механизму берут отсчет u 1 и записывают в таблицу 15.1, затем контур плавно обводят точкой М и завершают обвод в точке К и берут отсчет u 2 (желательно обводить против часовой стрелки, в этом случае последовательные значения отсчетов u i уменьшаются и это удобно для вычислений). Разность отсчетов u 1 – u 1 = n 1 представляет площадь в делениях планиметра.
Продолжают обводы, берут отсчеты u i (см. табл. 15.1) и вычисляют разности отсчетов n i , которые не должны различаться между собой более чем на две единицы при n ≤ 200, на четыре при n ≤ 1000, на шесть при n ≤ 2000. Вычисляют среднюю площадь n в делениях планиметра.
Если плюс расположен вне фигуры, ее площадь в масштабе плана вычисляется по формуле
Источник