Как найти периметр трапеции все способы

Формула периметра трапеции

Трапе́ция (от др. -греч. τράπέζιου — «столик» ; τράπεζα — «стол, еда» ) — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна. Иногда трапеция определяется как четырёхугольник, у которого произвольная пара противолежащих сторон параллельна, в этом случае параллелограмм является частным случаем трапеции

Периметр произвольной трапеции

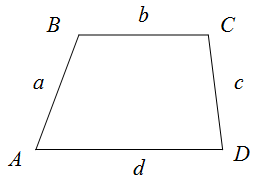
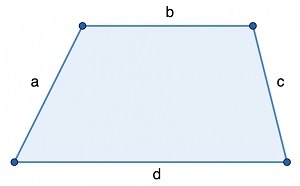
Периметр произвольной трапеции, в которой AB=a , BC=b , CD=c , AD=d , имеет вид:

\[ \LARGE P_ = a + b + c + d \]

где:
P — периметр трапеции
a, b, c, d — стороны трапеции

Периметр равнобокой трапеции

Равнобедренная трапеция — это трапеция у котрой боковые стороны равны.

Периметр произвольной трапеции, в которой AB=CD=a , BC=b , AD=c , имеет вид:

\[ \LARGE P_ = 2 \cdot a + b + c \]

где:
P — периметр трапеции
a, b, c, d — стороны трапеции

Признаки равнобедренной трапеции

Трапеция будет равнобедренной если выполняется одно из этих условий:

1. Углы при основе равны: ∠ABC = ∠BCD и ∠BAD = ∠ADC

2. Диагонали равны: AC = BD

3. Одинаковые углы между диагоналями и основаниями: ∠ABD = ∠ACD , ∠DBC = ∠ACB , ∠CAD = ∠ADB , ∠BAC = ∠BDC

4. Сумма противоположных углов равна 180°: ∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°

5. Вокруг трапеции можно описати окружность

Также можно найти периметр трапеции, не зная длин оснований, но имея среднюю линию m . Средняя линия по определению представляет собой полусумму оснований трапеции, поэтому умножив ее на два, можно подставить ее вместо оснований в формулу периметра: \( P = 2 \cdot m + c + d \) .

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

Источник

Нахождение периметра трапеции: формула и задачи

В данной публикации мы рассмотрим, каким образом можно посчитать периметр трапеции и разберем примеры решения задач.

Формула вычисления периметра

Периметр (P) трапеции равняется сумме длин всех ее сторон.

P = a + b + c + d

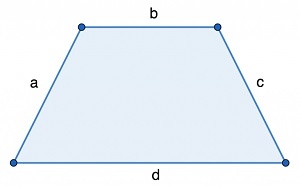
• b и d – основания трапеции;
• a и с – ее боковые стороны.

Периметр равнобедренной трапеции

В равнобедренной трапеции боковые стороны равны (a=c), из-за чего ее, также, называют равнобокой. Периметр считается так:

P = 2a + b + d или P = 2с + b + d

Периметр прямоугольной трапеции

Для расчета периметра используется такая же формула, что и для разносторонней трапеции.

P = a + b + c + d

Примеры задач

Задание 1
Найдите периметр трапеции, если ее основания равны 7 и 10 см, а боковые стороны – 4 и 5 см.

Решение:
Используем стандартную формулу, подставив в нее известные нам длины сторон: P = 7 см + 10 см + 4 см + 5 см = 26 см.

Задание 2
Периметр равнобедренной трапеции равняется 22 см. Найдите длину боковой стороны, если основания фигуры равны 3 см и 9 см.

Решение:
Как мы знаем, периметр равнобедренной трапеции вычисляется по формуле: P = 2a + b + d, где а – боковая сторона.
Ее длина, умноженная на два равна: 2a = P – b – d = 22 см – 3 см – 9 см = 10 см.
Следовательно, длина боковой стороны составляет: a = 10 см / 2 = 5 см.

Источник

Как найти периметр трапеции

Формула

Чтобы найти периметр трапеции необходимо найти сумму длин её сторон.

В общем случае для произвольной трапеции $ABCD$ со сторонами $AB=a$, $BC=b$, $CD=c$, $AD=d$ периметр вычисляется по формуле:

Если трапеция $ABCD$ равнобокая, то по определению её боковые стороны равны $AB=CD=a$ и формула для нахождения периметра примет вид:

Примеры вычисления периметра трапеции

Задание. Найти периметр трапеции $ABCD$ со сторонами $AB=1,5$ см, $BC=2$ см, $CD=1$ см, $AD=3$ см.

Решение. Для нахождения периметра трапеции $ABCD$ воспользуемся формулой

Подставляя в неё заданные в условии длины сторон, получим:

Ответ. $P_<\Delta A B C D>=7,5$ (см)

Как найти периметр трапеции не по зубам? Тебе ответит эксперт через 10 минут!

Задание. Заданна равнобокая трапеция $ABCD$ с основаниями $BC=3$ см, $AD=7$ см и высотой $BK=2 \sqrt<3>$ см. Найти периметр заданной трапеции.

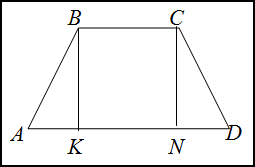
Решение. Сделаем рисунок.

Опустим высоту $CN$. Полученный в результате четырехугольник $BCKN$ является прямоугольником, поэтому $BC=KN$. Треугольники $\Delta A B K \quad$ и $\quad \Delta N C D$ — прямоугольные и равны между собой. Тогда $AK=ND$. Найдем чему равно $AK$:

$A K=(A D-B C): 2 \Rightarrow A K=(7-3): 2=2$ (см)

Из $\Delta ABK$ по теореме Пифагора найдем боковую сторону $AB$ трапеции:

Тогда периметр рассматриваемой равнобокой трапеции

Ответ. $P_<\Delta A B C D>=18$ (см)

Источник

Как найти периметр трапеции

​Трапеция — это четырехугольник, у которого лишь одна пара противолежащих сторон параллельна.

Периметр трапеции — это сумма длин всех его сторон.

Основные свойства трапеции

• средняя линия трапеции параллельна ее основаниям, а также равна половине их суммы;

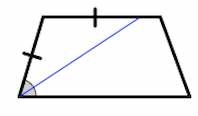
• биссектриса любого угла данного четырехугольника отсекает на его основании отрезок, равный боковой стороне;

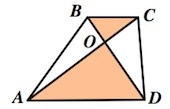
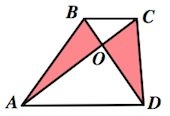
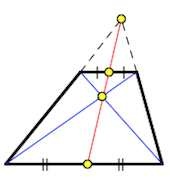
• треугольники ABO и DCO (на картинке), образованные диагоналями фигуры и ее основаниями, подобны;

• треугольники OAB и OCD, образованные диагоналями трапеции и ее боковыми сторонами, имеют одинаковую площадь;

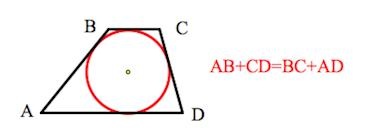
• если сумма длин оснований четырехугольника равна сумме его боковых ребер, то в фигуру можно вписать окружность;

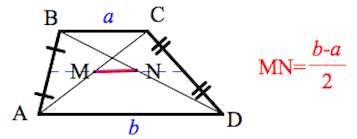
• точки M и N середины диагоналей лежат на одной прямой со средней линией фигуры. Также отрезок MN равен полуразность оснований четырехугольника;

• середины оснований фигуры, точка пересечения ее диагоналей, а также точка пересечения продолжений ее боковых сторон лежат на одной прямой;

Свойства равнобедренной трапеции

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

• в равнобедренной трапеции углы при обоих ее основаниях одинаковы;
• диагонали равны;
• равнобедренную трапецию всегда можно вписать в окружность или описать окружность вокруг;
• если диагонали перпендикулярны, то высота фигуры равна полусумме ее оснований.

Способы нахождений периметра

Рассмотрим способы, с помощью которых можно найти сумму длин всех сторон данного четырехугольника.

По всем сторонам

Формула для нахождения периметра выглядит так:

где a, b, c, d — стороны трапеции.

По сторонам равнобедренной трапеции

Если нам известны ребра этого четырехугольника с одинаковыми боковыми сторонами, то находить ее P можно по следующей формуле:

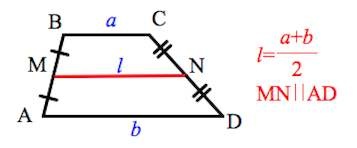
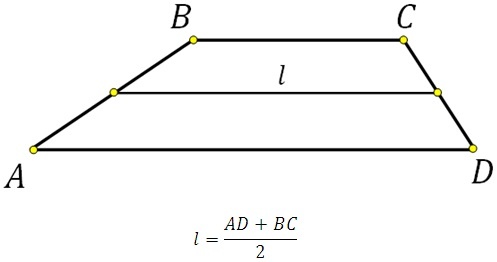
Через среднюю линию

Так как средняя линия трапеции равна полусумме ее оснований, то формулу P можно выразить так:

где l — средняя линия фигуры.

Примеры решения задач

Давайте рассмотрим наглядные примеры решения задач на нахождение суммы длин всех ребер этой фигуры.

Задача 1

Дана трапеция с боковыми сторонами 4 см и 5 см, а ее основания равны 7 см и 10 см. Найти периметр данного многоугольника.

Решение:

Нам пригодится самая первая формула для расчета:

Подставляем значения и получаем:

Задача 2

Известно, что у трапеции две боковые стороны равны 7 см, а ее основания равны 5 см и 8 см. Нужно найти P четырехугольника.

Решение:

Так как трапеция равнобедренная, удобнее всего будет использовать формулу:

Таким образом, получается:

\(P=2\times 7+5+8=27\) см.

Задача 3

Средняя линия l трапеции равна 6 см, а боковые стороны 5 см и 9 см. Вычислить P фигуры.

Источник

Периметр трапеции

Периметр трапеции часто нужно определить в задачах по геометрии. Периметр трапеции определяется также как и периметр любой другой фигуры на плоскости:

Периметр плоской фигуры — есть сумма всех сторон фигуры.

Чему равен периметр равнобедренной трапеции — то же самое — сумме всех ее сторон.

Найти периметр трапеции в задачах ЕГЭ

В задачах ЕГЭ вы найдете периметр трапеции. Например,

Задача 1

Около окружности описана трапеция, периметр которой равен 60. Найдите длину ее средней линии.

Решение:

В четырехугольник можно вписать окружность тогда и только тогда, когда суммы противолежащих сторон равны:

Где P_ABCD — периметр трапеции. В самом деле P_ABCD =AD+CB+DC+AB=2(DC+AB), а значит, DC+AB=P_ABCD /2

Средняя линия трапеции — это полусумма ее оснований, то есть MN=(DC+AB)/2=(P_ABCD /2)/2=P_ABCD /4 = 60/4=15 .

Ответ: 15.

Задача 2

Около окружности описана трапеция, периметр которой равен 44. Найдите длину ее средней линии.

Решение. Рассуждаем аналогично и получаем MN=(DC+AB)/2=(P_ABCD /2)/2=P_ABCD /4 = 44/4=11.

Ответ: 11.

То есть мы сами с вами вывели лайфхак для решения этой задачи:

И обратный лайфхак:

Применим наш лайфхак 1 к решению следующей задачи?

Задача 3

Около окружности описана трапеция, периметр которой равен 30. Найдите длину ее средней линии.

Ответ: 7,5.

Задача 4

Периметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 37, найдите радиус окружности.

Решение. Периметр трапеции равен: АD+DC+CB+AB=P_ABCD (1)

В трапецию можно вписать окружность, если суммы длин противоположных сторон равны. То есть, имеем: AD+CB=DC+AB (2)

С учетом (2) равенство (1) можно записать в виде: 2(АD+CB)=P_ABCD (3)

Теперь давайте посмотрим на вот такой рисунок:

Видно, что сторона AD=2R, где R — радиус окружности.

Тогда, AD+CB=2R+37, тогда равенство (3): 2(2R+37)=100.

Решаем уравнение, относительно R:

Ответ: 6,5

Задача 5

Из сборника ЕГЭ по математике профильный уровень 2020 год вариант 19 задание 6.
Около окружности описана трапеция, периметр которой равен 28. Найдите длину ее средней линии.
Решение: пользуясь лайфхаком, который мы вывели выше, вычисляем длину средней линии трепеции: делим периметр трапеции на 4.
Получаем 28:4=7
Ответ: 7.

Источник