Как найти периметр прямоугольника квадрата предложите разные способы

Как найти периметр фигуры

О чем эта статья:

Определение периметра

Периметром принято называть длину всех сторон многоугольника. Какой буквой обозначается периметр — заглавной латинской P. Под обозначением «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.

Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

Формула нахождения периметра

Рассмотрим пять фигур.

Треугольник

Периметр треугольника — это сумма длин трех его сторон.

P = a + b + c, где a, b, c — длина стороны.

Формула измерения периметра для равностороннего треугольника — это произведение длины стороны на три.

P = 3 * a, где a — длина стороны.

Квадрат и ромб

Периметр квадрата — это произведение длины стороны на четыре. Формула ромба выглядит идентично.

P = 4 * a, где a — длина стороны.

Прямоугольник и параллелограмм

Периметр прямоугольника — сумма длины и ширины, умноженная на два. Формула параллелограмма выглядит соответственно.

P = 2 * (a + b), где a — ширина, b — высота.

Записывайтесь на онлайн уроки по математике к лучшим преподавателям! Уроки для учеников с 1 по 11 классы!

Равнобедренная трапеция

Формула для равнобедренной трапеции отличается от прямоугольника тем, что у первого есть две равные стороны.

P = a + b + 2 * c, где a, b — параллельные стороны, c — две длины одинаковых сторон.

Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.

L = d * π = 2 * r * π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!

Решение задач

Площадь прямоугольника равна 80 см 2 , длина составляет 10 см. Чему равен периметр фигуры?

• Для использования формулы P = 2 * (a + b), нам нужно найти ширину;
• Так как S = a * b, для поиска одной стороны необходимо разделить площадь на известную сторону: 80 : 10 = 8 см;
• Далее подставляем известные переменные в формулу: (10 + 8) * 2 = 36 см;

Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?

• Используя формулу P = a + b + c вычислим сумму двух неизвестных сторон: 40 — 6 = 34 см;
• Известно, что равнобедренный треугольник имеет две равные стороны;
• Далее делим получившуюся сумму на два: 34 : 2 = 17 см;

Ответ: две другие стороны равны 17см.

Круг вписан в квадрат, его сторона равна 20 см. Найти периметр круга.

• Периметр круга равен длине ограничивающей его окружности. Значит P = L = d * π;
• Сторона квадрата для круга является диаметром, поэтому P = 20 * 3,14;

Источник

Как найти периметр квадрата

О чем эта статья:

2 класс, 3 класс

Основные определения

Квадратом принято называть правильный четырёхугольник, у которого равны все углы и стороны. Это частный случай прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов.

Периметр — это длина всех сторон многоугольника. Общепринятое обозначение — заглавная латинская буква P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.

Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

• квадратный миллиметр (мм 2 );
• квадратный сантиметр (см 2 );
• квадратный дециметр (дм 2 );
• квадратный метр (м 2 );
• квадратный километр (км 2 );
• гектар (га).

Формула нахождения периметра квадрата

Как находится периметр квадрата, всегда зависит от исходных данных. Рассмотрим две формулы, которые проходят 2 и 3 класс.

Если известна длина стороны

P = a + a + a + a, где a — сторона.

Так как все стороны фигуры равны, можно использовать формулу в таком виде: P = 4 * a

Если известна длина диагонали

P = d * 2 * √2, где d — диагональ.

Диагональ — это отрезок, который соединяет противоположные стороны фигуры.

Математика, как и любой другой предмет не сразу дается легко. Сложности могут возникать из-за неумения быстро делать простые арифметические действия — именно поэтому полезно практиковаться в решении примеров, как можно чаще. Давайте сделаем это прямо сейчас!

Занимайся изучением математики онлайн! Курсы по математике для учеников с 1 по 11 классы!

Решение задач

1. Найти периметр квадрата, диагональ которого равняется √4 см.

• Воспользуемся формулой P = d * 2 * √2;
• P = √4 * 2 * √2;

2. Найти периметр квадрата со стороной 97 мм. Записать ответ в сантиметрах

• Воспользуемся формулой P = 4 * a;
• P = 4 * 97

3. Периметр квадрата 48 см. Чему равна его сторона?

• Воспользуемся формулой P = 4 * a;
• Значит a = P : 4;
• a = 48 : 4;

4. Периметр квадрата 20 см. Как найти его площадь?

• Воспользуемся формулой P = 4 * a;
• Тогда a = P : 4;
• a = 20 : 4 = 5 см;
• Воспользуемся формулой S = a * a;
• Значит S = 5 * 5;

Источник

Как найти периметр прямоугольника

О чем эта статья:

Основные определения

Прямоугольником принято называть четырехугольник, у которого равны все углы. Они также являются прямыми и составляют 90°.

Периметр — это длина всех сторон многоугольника. Общепринятое обозначение — заглавная латинская буква P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.

Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

Формула нахождения периметра прямоугольника

Способ вычисления нужно выбрать, отталкиваясь от исходных данных. Далее рассмотрим четыре классические формулы.

Когда известны все или две соседние стороны

P = a + b + c + d, где a, b, c, d — стороны.

Когда известна любая сторона и площадь

P = 2 * (a + S : a), где a — сторона, S — площадь.

Площадь — это плоскость внутри замкнутой геометрической фигуры.

Когда известна любая сторона и диагональ

P = 2 * (a + √(d 2 — а 2 )), где a — сторона, d — диагональ.

Диагональ — это отрезок, который соединяет противоположные стороны фигуры.

Когда известна одна любая сторона и радиус описанной окружности

P = 2 * (a + √(4 * R 2 — a 2 )), где a — сторона, R — радиус окружности.

Радиус — отрезок, соединяющий центр и любую точку окружности.

Решение задач

А теперь практиковаться!

1. Одна сторона прямоугольника 9 см, а другая на 11 см длиннее. Как узнать периметр?

• Если a = 9, то b = 9 + 11;
• Тогда b = 20 см;
• Воспользуемся формулой P = 2 * (a + b);
• P = 2 * (9 + 20);

2. Площадь прямоугольника составляет 60 м², ширина равна 15 м. Чему равен периметр фигуры?

• Для использования формулы P = 2 * (a + b), нам нужно найти длину;
• Так как S = a * b, для поиска одной стороны необходимо разделить площадь на известную сторону: 60 : 15 = 4;
• Далее подставляем известные переменные в формулу: (15 + 4) * 2 = 38;

А еще можно вот так:

• Воспользуемся формулой P = 2 * (a + S : a);
• P = 2 * (15 + 60 : 15);

Ответ — такой же, 38 м.

3. Как найти периметр прямоугольника, если его диагональ в два раза больше длины равной 8 см?

• Если a = 8, то d = 8 *2;
• Тогда d = 16;
• Воспользуемся формулой P = 2 * (a + √(d 2 — а 2 ));
• P = 2 * (8 + √(16 2 — 8 2 ));

Источник

Периметр прямоугольника — формулы или способы расчетов

Началом пропедевтики изучения геометрии являются знания, которые учащиеся получают, переходя во 2 класс. Применяя правила умножения, здесь впервые вычисляют периметр прямоугольника.

Переходя в следующий, 3 класс, школьники на основе этой формулы начинают знакомиться с правилами раскрытия скобок.

Как вычислить периметр прямоугольника

Учитывая, что периметр любой фигуры есть сумма длин её сторон, выводят две формы записи для нахождения этой величины.

В прямоугольнике противоположные стороны равны, поэтому, обозначив смежные стороны a и b, получают по определению:

откуда после приведения подобных слагаемых, вытекает формула

или, вынося двойку за скобки,

Рассматривая квадрат, как прямоугольник с равными сторонами, получают формулу его периметра:

Стандартный метод

В зависимости от сложности вычислений, применяют одну из формул, чтобы высчитать периметр. Учащиеся начальной школы знакомятся с понятием, сталкиваясь с практическими задачами.

Задача

Найти длину забора участка прямоугольной формы, который надо построить Сидору Карловичу, если общая граница с участком Ивана Петровича составляет 3 метра, а с плантацией Марии Ивановны – 5 метров.

Решение

Чтобы решить задачу и помочь незадачливому Сидору Карловичу, ученику приходится использовать формулу периметра прямоугольника. Учитывая, что a = 3, b = 5, дети легко находят, что длина забора равна

P = 2 (a + b) = 2 * (3 + 5) = 2 * 8 = 16 (метров)

Важные требования, предъявляемые к ученикам на данном этапе изучения материала, заключаются в правильном соизмерении длины и ширины, а также в умении начертить фигуру.

Работа выполняется только при одинаковых единицах измерения, все чертежи делаются строго с использованием инструментов!

Часто длина заданного отрезка измеряется непосредственно.

Нахождение периметра через площадь и одну сторону

При более близком знакомстве с прямоугольником, способы нахождения его периметра начинают варьироваться в зависимости от исходных данных в задаче.

Если известны одна из сторон и площадь, то, чтобы узнать, чему равен периметр, выражается неизвестная сторона, а затем она подставляется в формулу.

то есть, соотношение площади и периметра при известной стороне есть

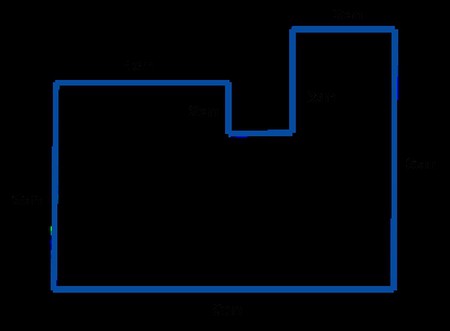
Как найти периметр прямоугольной фигуры

В начальной школе для запоминания принципа детям часто предлагается понятие «неправильного четырёхугольника» (не прямоугольника).

Для нахождения его периметра предлагается рассчитать сумму длин сторон непосредственно, предварительно измерив каждую из них.

Для любой более сложной фигуры производят разбиение, если возможно, на небольшие прямоугольники, с которыми и работают.

Заключение

Современный онлайн калькулятор позволяет ввести значения сторон и задать необходимую точность вычислений, мгновенно производя расчёт и выдавая необходимый результат.

Источник

Периметр квадрата и прямоугольника. Способы определения и примеры решения.

Часто на просторах интернета можно найти насмешки по поводу того, как знания по математике — интегралы, дифференциалы, тригонометрические функции и прочие разделы предмета — не помогают облегчить жизнь человека. Такие шутки напрасны, ведь как выручает умение правильно рассчитывать периметр квадрата, прямоугольника и других геометрических фигур в строительных работах. Расход материала: плитки, обоев, напольного покрытия — не определить без понимания элементарных математических формул и геометрических фигур.

Свойства квадрата

Любые вычисления в математике базируются на свойствах объекта. Чтобы ответить на вопрос: «Чему равен периметр квадрата?» — рекомендуется вспомнить отличительные характеристики этой фигуры.

1. Равенство всех сторон.
2. Наличие четырех углов величиной 90 градусов.
3. Параллельность сторон.
4. Поворотная симметрия. При вращении фигуры ее вид остается неизменным.
5. Возможность описать и вписать окружность.
6. Диагонали при пересечении делят друг друга пополам.
7. Площадь фигуры характеризует заполненное квадратом место в двухмерном пространстве.
8. Периметр фигуры не что иное, как сумма длин его сторон.
9. Из предыдущего свойства вытекает, что единицами измерения величины периметра будут единицы длины: м, см, дм и другие.

Для подсчета плинтусов для завершения ремонта в квадратном помещении, необходимо знать длину комнаты. Для этого необходимо посчитать ее периметр.

Периметр

В переводе с греческого языка слово означает «измерять вокруг». Термин применим ко всем замкнутым фигурам: квадрату, окружности, прямоугольнику, треугольнику, трапеции и прочим. Знания по определению периметра элементарных фигур необходимы для решения сложных геометрических задач с объектами неправильной формы. Например, для расчета плинтусов в комнату планировкой типа «Г», или как еще называют, «сапожком», потребуется определить периметр квадрата и прямоугольника. Ведь форма помещения состоит из этих элементарных фигур.

Общепринятое обозначение такой величины – буква Р. Каждой фигуре с учетом ее свойств присуща своя формула для определения периметра.

Свойства прямоугольника

1. Равенство противоположных сторон.
2. Равенство диагоналей.
3. Возможность описать окружность.
4. Высоты прямоугольника равны его сторонам.
5. Сумма углов равна 360 градусов, и все углы прямые.
6. Параллельность противоположных сторон.
7. Перпендикулярность прилегающих сторон.
8. Сумма квадратов диагоналей прямоугольника равна сумме квадратов его сторон.
9. Пересекаясь, диагонали делят друг друга пополам.
10. Невозможность вписать в фигуру окружность.

Периметр квадрата

В зависимости от установленных (известных) параметров квадрата, существуют разные формулы для определения его периметра. Простой задачей является расчет периметра при установленной длине его стороны (с). В этом случае Р=с+с+с+с или 4*с. Например, длина стороны квадрата 7 см, тогда периметр фигуры буде 28 см (4*7).

В первом случае все понятно, но как найти периметр квадрата, зная его площадь? И тут все предельно ясно. Поскольку площадь фигуры определяется умножением одной стороны на другую, а у квадрата все стороны равны, необходимо извлечь корень из известной величины. Пример: есть квадрат с площадью 25 дм 2 . Корень из 25 равен 5 – эта величина характеризует длину стороны квадрата. Теперь, подставляя найденную величину — 5 дм 2 — в первоначальную формулу периметра, можно решить задачу. Ответом будет значение в 20 дм. То есть 4 умножили на 5, получили искомую величину.

Квадрат и окружность

Из свойств рассматриваемой фигуры выплывает, что в квадрат можно вписать окружность и также ее описать вокруг фигуры.

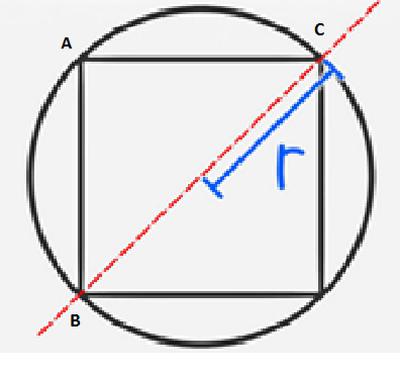
Первый вариант – нахождение периметра по радиусу описанной окружности. Вписанным считается квадрат, вершины которого находятся на окружности. Радиус окружности равен 1/2 длине диагонали. Выходит, что диаметр равен диагонали. Теперь необходимо рассмотреть прямоугольный треугольник, который получился в результате деления диагональю квадрата. Решение задачи сводится к нахождению сторон этого треугольника. ВС – это известная величина, диаметр описанной окружности. Допустим, он равен 3 см. Теорема Пифагора в случае с равными сторонами треугольника, будет выглядеть так: 2с 2 =3 2 . В формуле обозначение с – это длина стороны треугольника и квадрата; 3 – известная величина гипотенузы. Отсюда, с=√9/2. Зная сторону квадрата, его периметр посчитать не проблема.

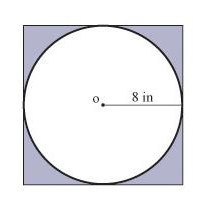
Особенностью вписанной окружности является деление сторон квадрата пополам. Поэтому радиус равняется половине длины стороны квадрата. Тогда сторона с=2*радиус. Периметр квадрата в этом случае равен 4*2*радиус или 8 радиусам окружности.

Периметр прямоугольника

Самая элементарная формула определения периметра прямоугольника через известные величины его сторон выглядит так: Р=2(а+b), где а и b — длины сторон фигуры.

Диагональ прямоугольника аналогично квадрату делит фигуру пополам, образуя прямоугольный треугольник. Однако задача усложняется тем, что стороны этого треугольника неравные. В случае с известной величиной одной из сторон и диагонали, вторую можно найти, следуя теореме Пифагора: д 2 =а 2 +в 2 , где а и в – стороны фигуры, а д – диагональ.

Если неизвестна ни одна из сторон, тогда в дело вступают знания тригонометрии: синусы, косинусы и другие функции.

Нахождение периметра по описанной окружности и известному диаметру сводится к тому, что диаметр равен длине диагонали фигуры. Дальше решение задачи определяется по наличию известных величин. Если даны углы, тогда через тригонометрические функции. Если дана сторона, ответ будет найден через теорему Пифагора.

Прямоугольник и тригонометрические функции

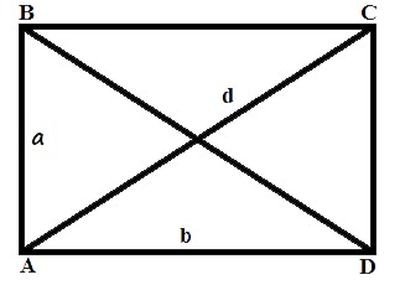
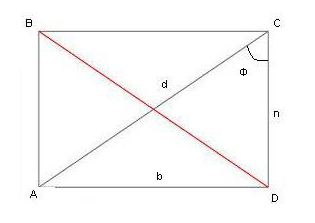
Для наглядности приведен пример решения задачи. Дано: прямоугольник АВСД; длина диагонали (d) 20 см; угол ф – 30°. Найти периметр фигуры.

Из тригонометрии необходимо вспомнить следующее: синус угла в прямоугольном треугольнике равен отношению противоположного катета к гипотенузе. Синус 30° (существуют таблицы, по которым можно определить значения тригонометрических функций для правильных углов) равен 1/2. Получается 1/2 = отношению в к d. Неизвестная величина в будет равна d/2=20/2=10 см.

Для расчета периметра следует найти вторую сторону фигуры. Можно через теорему Пифагора, так как известны длины гипотенузы и одного из катетов или опять через отношение сторон для косинуса угла.

Косинус угла ф выражается как отношение прилежащего катета к гипотенузе и равен √3/2.

√3/2=n/d, n=(d*√3)/2 или 10*√3. После извлечения корня из 3, получаем длину стороны треугольника: 10*1,73=17,3 см.

Периметр равен 2(17,3+10)=2*27,3=54,6 см.

Периметр и отношение сторон

В школьной программе встречаются задачи по геометрии, когда длины сторон прямоугольника выражены их отношением друг к другу. Рассмотрение решения подобной задачи представлено ниже.

Известно, что сумма длин всех сторон прямоугольника, то есть его периметр, равен 84 см. Отношение длины (д) к ширине (ш) – 3:2. Найти стороны фигуры.

Решение: пусть длина будет 3х, а ширина 2х, согласно соотношению из условия задачи. Формула периметра прямоугольника с полученными данными длин сторон будет следующей: 3х+3х+2х+2х = 84. Далее, 10х = 84, х=8,4 см. Подставив х в выражение длины и ширины прямоугольника, можно найти искомые величины. Длина будет: 3*8,4 = 25,2 см; ширина: 2*8,4 = 16,8 см.

Статья посвящена решению наиболее часто встречаемых задач в школьной программе. И это далеко не все способы нахождения периметра квадрата и прямоугольника.

Источник