Как найти натуральную величину треугольника все способы

Определить натуральную величину треугольника ABC

Здравствуйте!
Что такое натуральная величина треугольника и как определить натуральную величину треугольника АВС?
Очень нужны примеры.
Спасибо!

Разберем что такое натуральная величина треугольника и как определить натуральную величину треугольника АВС.
Задание определения натуральной величины плоской фигуры относят к метрическим задачам.
Натуральную величину треугольника на эпюре Монжа можно определить несколькими способами. Рассмотрим некоторые из них.

1. Способ прямоугольного треугольника

Необходимо поочередно применять этот способ, чтобы определить действительные величины отрезков, которые составляют треугольник, а далее методом засечек к одному из них строят два других.
Коротко о способе прямоугольного треугольника:
Данный способ применяют, чтобы определить натуральные величины отрезков и углов наклона этих отрезков к плоскостям проекций. Для этого нужно выполнить построение прямоугольного треугольника, один катет которого будет одной из проекций отрезка. Другой катет будет разностью глубин или высот конечных точек отрезка, а гипотенуза будет натуральной величиной.

1. Плоскопараллельное перемещение

1. Вращение вокруг перпендикулярных к плоскостям проекций осей

http://ru.solverbook.com/img_questions/16.02__15_1.jpg

1. Способ вращения вокруг горизонтали, являющихся линиями уровня

или вокруг фронтали, являющихся линиями уровня

1. Способ вращения вокруг следа (или совмещение с плоскостью проекций)

1. Способ перемены плоскости проекции

Источник

Определение натуральной величины отрезка

Если отрезок параллелен плоскости, то он проецируется на неё без искажений. В остальных случаях для нахождения его натуральной величины применяют метод прямоугольного треугольника или способы преобразования ортогональных проекций.

Метод прямоугольного треугольника

Сущность данного метода заключается в нахождении гипотенузы прямоугольного треугольника, у которого один катет равен горизонтальной (или фронтальной) проекции отрезка, а величина другого катета представляет собой разность удаления концов отрезка от горизонтальной (или, соответственно, фронтальной) плоскости проекции.

Для того чтобы найти натуральную величину отрезка AB (рисунок выше), строим прямоугольный треугольник A₀A’B’. Его первый катет A’B’ – это горизонтальная проекция AB. Второй катет A’A₀ равен величине Z_A – Z_B, то есть разности удаления точек A и B от горизонтальной плоскости П₁.

Откладываем A’A₀ = Z_A – Z_B перпендикулярно A’B’. Затем проводим гипотенузу A₀B’ треугольника A₀A’B’. На рисунке она обозначена красным цветом. Её величина соответствует настоящей длине AB.

Способ параллельного переноса

Параллельный перенос представляет собой перемещение геометрической фигуры параллельно одной из плоскостей проекций. При этом величина проекции фигуры на эту плоскость не меняется. Например, если перемещать отрезок EF параллельно горизонтальной плоскости П₁, то длина его проекции E’F’ не изменится, когда она займет новое положение E’₁F’₁ (как это показано на рисунке ниже).

Еще одно важное свойство параллельного переноса заключается в том, что при любом перемещении точки параллельно горизонтальной плоскости проекции, её фронтальная проекция движется по прямой, параллельной оси X. Если точка перемещается параллельно фронтальной плоскости, то её горизонтальная проекция движется по прямой, параллельной оси X.

Чтобы определить действительный размер отрезка EF, на свободном месте чертежа строим его новую горизонтальную проекцию E’₁F’₁ = E’F’ так, чтобы она была параллельна оси X . Затем по линиям связи находим точки E»₁ и F»₁. Расстояние между ними и есть искомая величина, поскольку мы перенесли EF в положение, параллельное фронтальной плоскости.

Метод параллельного переноса, описанный здесь, иногда называют параллельным перемещением. Посмотреть дополнительные примеры и получить более подробную информацию по данной теме можно в этой статье.

Поворот вокруг оси

Для того, чтобы отрезок стал параллелен плоскости проекции и без искажения отразился на ней, он может быть повернут вокруг проецирующей прямой, проходящей через один из его концов.

Определим длину произвольного отрезка MN. Для этого через точку N проводим горизонтально проецирующую прямую i. Вокруг неё поворачиваем MN так, чтобы его проекция M’N’ заняла положение M’₁N’₁, параллельное оси X.

По линиям связи находим точку M»₁. При этом исходим из того, что M» в процессе вращения движется параллельно горизонтальной плоскости.

Точка N не изменит своего положения, так как лежит на оси поворота. Поэтому осталось только соединить N»₁ и M»₁ искомым отрезком. На рисунке он выделен красным цветом.

Более подробную информацию о решении задач методом поворота вокруг оси вы можете получить, ознакомившись со следующим материалом.

Источник

Как найти натуральную величину треугольника

— можно способами преобразования чертежа, которые переводят заданный треугольник в положение параллельное одной из плоскостей проекций.

Способ совмещения вращением вокруг следа плоскости

Продлевая стороны треугольника до горизонтальной плоскости проекций получаются точки 1 и 2 лежащие на горизонтальном следе h α плоскости треугольника. Фронтальный след f α построен из точки схода следов и точки 3 которая соответствует пересечению BC с фронтальной проекцией.

На фронтальном следе произвольно выбрана точка F. При вращении плоскости треугольника вокруг горизонтального следа, каждая точка плоскости описывает окружность лежащую в вертикально проецирующей плоскости, которая перпендикулярна горизонтальному следу. При совмещении плоскости треугольника с горизонтальной плоскостью проекций, точка F должна быть удалена от точки схода следов X_0α на расстояние равное удалению по фронтальной проекции фронтального следа. Фактически, горизонтальная проекция F в совмещённом положении строится как пересечение дуги с центром в точке схода следов и горизонтальной проекции траектории движения при повороте.

Серия горизонталей h проведена через вершины треугольника на фронтальной проекции до пересечения с фронтальным следом. По точкам пересечения со следом, горизонтали перенесены на плоскость совмещённую с горизонтальной проекцией. При вращении треугольника вокруг горизонтального следа, вершины перемещаются по окружностям в плоскостях перпендикулярных горизонтальному следу. Пересечения горизонтальных проекций траекторий вращения вершин с горизонтальными проекциями горизонталей определяют точки треугольника совмещёнными с горизонтальной плоскостью проекций. Таким образом, A 0
1 B 0
1 C 0
1 — найденная Натуральная величина треугольника.

Замена плоскостей проекций

В плоскости треугольника проведена фронталь f. Перпендикулярно фронтали построена плоскость проекций П₅, заменяющая П₁. На П₅ треугольник проецируется в отрезок. Вторая замена параллельно треугольнику A₆B₆C₆=АВС .

Плоскопараллельное перемещение

Плоскопараллельным перемещением выполнено треугольник перемещён до положения горизонтально проецирующего f⊥П₁. Первое перемещение преобразовывает горизонтальную проекцию треугольника в отрезок прямой. Второе перемещение производится до положения параллельно фронтальной плоскости.

Метод прямоугольного треугольника

Методом прямоугольного треугольника можно найти натуральную величину расстояния от прямой линии лежащей в плоскости треугольника до вершин. Если в качестве этой линии выбрать горизонталь или фронталь, то используя натуральную величину можно построить треугольник равный заданному но лежащий в плоскости параллельной горизонтальной или фронтальной проекции. Соответственно, проекция построенного треугольника окажется равной натуральной величине.

При вращении треугольника вокруг фронтали f, вершины перемещаются по окружностям во фронтально проецирующих плоскостях. Фронтальные проекции траектории вращения вершин треугольника представлены перпендикулярами к f. Радиус вращения вершин построен методом прямоугольного треугольника. B 0
2 — положение вершины в плоскости параллельной фронтальной проекции и проходящей через ось вращения — фронталь.

Источник

Натуральная величина треугольника

Цель видеоурока Автокад/НГ: Обучение Автокад 2D на практике и закрепление пройденного материала раздела «Теоретические и практические видеоуроки Автокад». Закрепление знаний по решению задач на построение натуральной величины отрезка, треугольника, сечения и т.д. используя для этого любой способ преобразования чертежа.

Задание: Определить натуральную величину треугольника ABC.

Дано: Таблица значения координат.

Вариант	Значения координат
	XA	YA	ZA	XB	YB	ZB	XC	YC	ZC
1	90	90	10	140	90	70	160	20	30

Для определения натуральной величины треугольника ABC воспользуемся способом преобразования проекций – вращение плоскости вокруг оси.

Источник

Чертежик

Метки

Натуральная величина треугольника с описанием.

Натуральная величина треугольника определяется 2 методами:

1. замена плоскостей проекции;
2. плоскопараллельное перемещение.

Это задание является обязательным для студентов в учебных заведениях и для его решения необходимо изучить тему: » Способы преобразования чертежа».

Для наглядности я использовал определенное задание и на его примере покажу как находится натуральная величина треугольника.

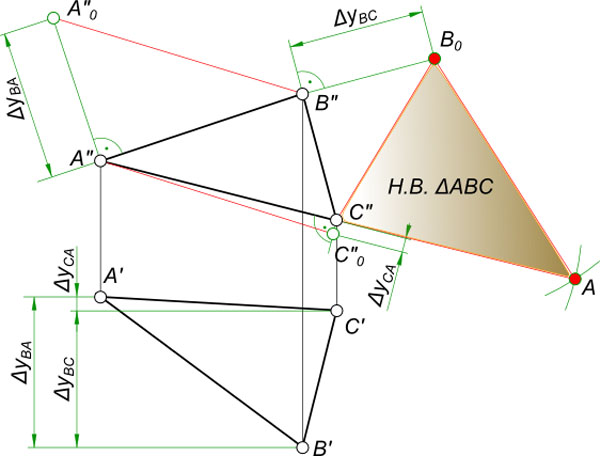
Алгоритм определения натуральной величины плоскости:

Замена плоскостей проекции

1.) Для построения чертежа использовал задание, расположенное снизу. Первоначально строятся точки по координат в плоскостях П1 и П2.

2.) Строится дополнительная горизонтальная линия 1 1 в верхнем изображении (проводится линия от средне расположенной точки по высоте), затем опускают дополнительные отрезки на нижнее изображение (как указано на рисунке снизу) и соединяют прямой. Эта прямая необходима для того, чтобы на ней расположить вспомогательную плоскость.

3.) Построив прямую на нижнем рисунке, чертится под углом 90 0 ось Х 1 (от точки С1 располагаем на произвольном расстоянии, но не слишком далеко). Затем отмеряются расстояния:

• от С2 до оси Х;
• от В2 до оси Х;
• от А0 до оси Х.

Полученные размеры откладываются от оси Х1 (размеры указаны разными цветами на рисунке снизу) и соединяют, далее подписываются точки.

4.) Строится еще одна дополнительная ось Х2, расположенная параллельно отрезку В 4 С 4 А 4. От точек В4,С4 и А4 проводят прямые перпендикулярные оси Х2.

5.) Отмеряются расстояния:

• от В1 до Х1;
• от С1 до Х1;
• от А1 до Х1.

Полученные результаты измерений откладываются от иси Х2 (на изображении снизу отмечены зелеными и голубым цветами).

6.) Соединяются точки и подписывают полученную плоскость заглавными «Н.В.»

Плоскопараллельное перемещение

7.) Откладывается отрезок на оси Х (обозначен синим цветом).

8.) Переносятся точки на текущее построение.

9.) Соединяют точки, получившиеся при переносе из плоскостей проекций. 10.) Методом вращения точки А2′, С2′ переносятся на горизонтальную прямую, а точка В2′ не меняет свое положение (относительно ее и происходило вращение).11.) Откладывается точка (располагают от оси Х на небольшом расстоянии, т.е. произвольном), относительно которой и будет откладываться плоско параллельное перемещение плоскости. 12.) От точек А2′, С2′ и В2′ опускаются прямые. Далее циркулем необходимо отмерить расстояния:

Затем эти размеры откладываются от С1′ (обозначены красным и синим цветами).

13.) Соединяются и подписываются точки (А1′, В1′ и С1′). Опускают прямые от С2″ и А2″14.) От точек С1 и А1 отводят прямые до пересечения с прямыми опущенными от точек С2″ и А2″. В месте пересечения ставится точка.15.) Завершающим шагом является соединение точек и обводка линиями всего чертежа.Пример чертежа на тему «Натуральная величина треугольника» смотрите здесь.

Источник