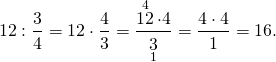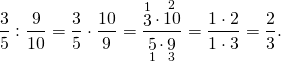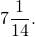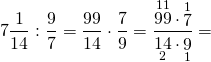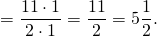Как найти число по данному значению его дроби 2 способа

Как найти число по заданному значению его дроби

Нахождение числа по заданному значению его дроби

Дробь — вариант записи числа в математике.

Дроби разделяют на следующие виды:

Запись числа в виде обыкновенной дроби предполагает написание числа, представленного в виде числителя, поделенного на знаменатель. Знак, отделяющий числитель от знаменателя, называют дробной чертой. Дробная черта подразумевает знак деления.

Числитель — число над дробной чертой в обыкновенной дроби.

Знаменатель — число под дробной чертой в обыкновенной дроби.

Если числитель равен знаменателю, то дробь превращается в единицу.

Если числитель меньше знаменателя, то дробь правильная.

Если числитель больше знаменателя — неправильная.

Обыкновенные дроби: 4 5 , 6 11 , 12 7 .

Среди обыкновенных дробей выделяют смешанные числа вида 3 4 5

В этой записи числа 3 обозначает целую часть, 4 — числитель, 5 — знаменатель.

Чтобы перевести смешанное число в обыкновенную дробь, нужно:

1. В числителе записать число, которое получают по схеме: целую часть умножить на знаменатель и прибавить числитель.
2. Знаменатель дроби оставить без изменений.

Полученная дробь называется неправильной. У нее числитель будет больше знаменателя.

Перевести смешанное число 3 4 5 в неправильную дробь.

3 4 5 = 3 * 5 + 4 5 = 19 5 .

Десятичные дроби записываются с помощью знака запятой, отделяющей целую часть от дробной части.

Десятичные дроби: 7,346;\;0,97;\;0,0001.

Вася съел 3 7 пиццы, что составляется 6 кусков. Найдите, на сколько частей разделена пицца.

Пусть вся пицца равняется x. Тогда по условию задачи: 3 7 пиццы (x) равны трем кускам, получим уравнение 3 7 x = 6 .

Из этого уравнения находим x, выраженный неизвестным множителем. Для этого нужно произведение разделить на известный множитель.

Получим: x = 6 : 3 7 .

Чтобы натуральное число разделить на обыкновенную дробь, нужно:

1. Переписать натуральное число, а знак деления заменить на знак умножения.
2. Умножить натуральное число на дробь, которая будет взаимно обратной данной.

Взаимно обратными называются дроби, произведение которых дает единицу.

Дробь, являющаяся взаимно обратной дроби 3 7 — это 7 3 .

Тогда 6 умножаем на 7 3 .

Чтобы умножить число на обыкновенную дробь:

1. Натуральное число представляем в виде дроби со знаменателем 1.

1. Умножаем полученные дроби: числитель умножаем на числитель, знаменатель на знаменатель.

6 1 * 7 3 = 6 * 7 1 * 3 .

1. Сокращаем полученную дробь: ищем такое число, на которое делится и числитель, и знаменатель нацело (без остатка).

6 и 3 делятся нацело на 3.

6 * 7 1 * 3 = 2 * 7 1 * 1 = 14 1 = 14

Вся цепочка решения:

x = 6 : 3 7 = 6 1 : 3 7 = 6 1 * 7 3 = 6 * 7 1 * 3 = 2 * 7 1 * 1 = 14 1 = 14 .

Получаем, что пицца состоит из 14 кусков.

Ответ: пиццу разделили на 14 частей.

Основные правила, описание алгоритма

Нахождение числа по заданному значению его дроби можно свести к следующему правилу: значение делим на дробь.

5 6 числа равны 20. Найдите это число.

Воспользуемся правилом: чтобы найти число по заданному значению его дроби, нужно значение разделить на дробь.

Получим: 20 : 5 6 .

Чтобы число разделить на обыкновенную дробь, нужно натуральное число умножить на дробь, взаимно обратную данной.

Дробь, которая будет взаимно обратной дроби 5 6 равна 6 5 .

Переводим натуральное число в дробь. Для этого представляем его в виде: 20 1 .

Получим выражение: 20 1 * 6 5 .

20 1 * 6 5 = 20 * 6 1 * 5 .

Сокращаем дробь. Числитель и знаменатель делятся нацело на 5.

20 * 6 1 * 5 = 4 * 6 1 * 1 = 24 1 = 24 .

Вся цепочка решения: 20 : 5 6 = 20 1 : 5 6 = 20 1 * 6 5 = 20 * 6 1 * 5 = 4 * 6 1 * 1 = 24 1 = 24 .

Ответ: искомое число равно 24.

Также встречаются задания на нахождение числа по его проценту.

Процент — это сотая часть числа. Чтобы перевести проценты в число, нужно это число разделить на сто процентов.

Разберем алгоритм решения задач такого типа на примере.

Увеличив время на работу на 5%, Маша собрала на 2 подарка больше за неделю, чем планировала. Сколько подарков должна была собрать Маша изначально?

Переводим проценты в десятичную дробь. Для этого используем правило: данное число процентов (5%) делим на 100%. Получаем:

Теперь по правилу нахождения числа по значению его дроби, делим 2 на 0,05.

В выражении 2 — делимое; 0,05 — делитель.

Чтобы разделить натуральное число на десятичную дробь, нужно:

1. Избавиться от запятой в делителе. Для этого умножаем 0,05 на 100 — в дроби после запятой два знака, значит, умножаем на сто. Количество знаков после запятой в дроби соответствует количеству нулей после единицы в множителе.
2. Чтобы выражение осталось неизменным, нужно умножить на 100 и делимое.

1. Подставим в выражения измененные числа: 200 разделим на 5.
2. Считаем:

Вся цепочка решения: 2:0,05=(2*100):(0,05*100)=200:5=40.

Ответ: 40 подарков.

Получаем алгоритм нахождения числа по его проценту:

1 шаг — перевести процент в число: разделить число процентов на сто процентов.

2 шаг — разделить значение заданной части числа на полученное в первом шаге значение.

Примеры задач на дробные выражения для 6 класса

7 9 числа составляют 42. Найдите это число.

Пусть неизвестное число равняется x. Тогда 7 9 числа x равняются 42:

Задача свелась к решению уравнения. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.

7 9 x = 42 x = 42 : 7 9 Чтобы натуральное число разделить на обыкновенную дробь, представляем натуральное число в виде дроби со знаменателем 1 и умножаем ее а дробь, которая будет взаимно обратной дроби 7 9 . x = 42 1 * 9 7 Умножаем числитель на числитель, знаменатель на знаменатель: x = 42 * 9 1 * 7 Сокращаем дробь: ищем общий делитель числителя и знаменателя. Числитель и знаменатель делятся нацело на 7 42 делится нацело на 7 и 7 делится нацело на 7. x = 6 * 9 1 * 1 x = 54 1 x = 54 .

Используя материал урока, самостоятельно решите задание.

63% числа составляют 126. Найдите это число.

Переводим 63% в десятичную дробь. Получим 0,63.

Тогда 0,63 от искомого числа составляют 126. Обозначим искомое число за x.

0 , 63 x = 126 x = 126 : 0 , 63 Чтобы число разделить на десятичную дробь, избавляемся в делителе от запятой. Для этого каждый компонент выражения умножаем на сто. Получим: x = 12600 : 63 И считаем: x = 200 .

Ответ: искомое число — 200.

Иван прошел 250 метров, что составляет 4 7 местной экологической тропы. Какова протяженность экологической тропы?

Пусть длина всей экологической тропы равняется x метрам. Тогда получим уравнение для нахождения всего пути:

Чтобы найти неизвестный множитель x, делим произведение на известный множитель.

x = 250 : 4 7 Представляем натуральное число в виде дроби 250 1 . x = 250 1 : 4 7 Чтобы разделить две дроби друг на друга, первую дробь переписываем, знак деления меняем на знак\;умножения,\;вторую\;дробь\;«переворачиваем»\;(находим дробь, обратную данной). x = 250 1 * 7 4 Перемножаем числитель на числитель, знаменатель на знаменатель. x = 250 * 7 1 * 4 Сокращаем дробь: делим числитель и знаменатель на одно и то же число. 250 и 4 делятся на 2. x = 125 * 7 1 * 2 x = 875 2 Делим числитель на знаменатель. Получаем десятичную дробь: x = 437 , 5 .

Ответ: длина экологической тропы 437,5 метра.

Ирина одолела 25% заданий, что составляет 4 примера. Сколько примеров нужно решить Ирине.

Пусть суммарное количество примеров равняется x. Тогда 25% от x равняется 4.

Составим уравнение: 25%x=4.

Чтобы решить уравнение, нужно найти неизвестный множитель x: произведение разделить на известный множитель.

Переводим проценты в дробь: 25%:100%=0,25.

Получим уравнение: 0,25x=4.

0 , 25 x = 4 x = 4 : 0 , 25 Чтобы натуральное число разделить на десятичную дробь, домножаем каждый компонент на сто: x = 4 * 100 : 0 , 25 * 100 x = 400 : 25 x = 16 .

Получается, Ирине было задано решить 16 примеров, из которых 4 она уже решила. Значит, ей осталось решить:

Источник

Как найти число по его дроби

Правило нахождения числа по его дроби:

Чтобы найти число по данному значению его дроби, нужно это значение разделить на дробь.

Рассмотрим, как найти число по его дроби, на конкретных примерах.

1) Найти число, 3/4 которого равны 12.

Чтобы найти число по его дроби, это число делим на эту дробь. Чтобы разделить число на дробь , надо данное число умножить на число, обратное к дроби (то есть на перевернутую дробь). Чтобы умножить дробь на число , надо числитель умножить на это число, а знаменатель оставить без изменения. Сокращаем 12 и 3 на 3. Так как в знаменателе получили единицу, ответ — целое число.

2) Найти число, если 9/10 его равняются 3/5.

Чтобы найти число по данному значению его дроби, это значение делим на эту дробь. Чтобы разделить дробь на дробь, первую дробь умножаем на обратную ко второй (перевернутую). Чтобы умножить дробь на дробь, числитель умножаем на числитель, знаменатель — на знаменатель. Сокращаем 10 и 5 на 5, 3 и 9 — на 3. В результате получили правильную несократимую дробь, значит это — окончательный результат.

3) Найти число, 9/7 которого равны

Чтобы найти число по значению его дроби, это значение делим на эту дробь. Смешанное число переводим в неправильную дробь и умножаем его на число, обратное ко второму (перевернутую дробь). Сокращаем 99 и 9 на 9, 7 и 14 — на 7. Поскольку получили неправильную дробь, необходимо выделить из нее целую часть.

Источник

Урок 19 Бесплатно Нахождение числа по его дроби

В этом уроке мы научимся, зная дробь от числа, находить все число.

Также мы узнаем, как делать аналогичные действия для процентов, то есть по данному количеству процентов находить все число.

Потом применим полученные навыки для решения задач.

Нахождение числа по его дроби

Сформулируем, в чем состоит задача нахождения числа по его дроби.

Имеется дробь; она говорит о том, какая часть от числа нам дана.

Имеется число, равное данной дробной части от искомого числа.

Мы уже умеем находить дробь от числа. Вспомним как это делать.

Чтобы найти дробь от числа нам нужно исходное число умножить на эту дробь, тогда получится какое-то значение, обозначающее дробь от числа.

В этой задаче было известно все число и то, какую дробную часть от него необходимо получить. Дробь от числа оставалась неизвестной.

В задаче этого урока дробь от числа нам уже известна, а все число, напротив, только предстоит найти.

Для его нахождения можно составить уравнение, аналогичное тому, которое было на картинке выше. Отличие будет только в том, какие переменные нам известны.

Решая это уравнение, вы переносите известный нам множитель, то есть дробь, в правую часть.

Как делить на дробь мы изучили в прошлом уроке. Напомним, что для этого надо домножить на взаимно обратное число к этой дроби.

Итак, вы получили выражение для неизвестного числа.

Сформулируем правило: чтобы найти дробь от числа необходимо разделить известную часть числа на дробь.

Пример 1

\(\mathbf<\frac<3><4>>\) от числа равны 21-му, найдите исходное число.

Для решения необходимо разделить известную часть на дробь, то есть 21 разделить на \(\mathbf<\frac<3><4>>\)

Пример 2

\(\mathbf<\frac<2><7>>\) от числа равны 12, найдите исходное число.

Для решения надо разделить данную часть числа на данную дробь, то есть 12 разделить на \(\mathbf<\frac<2><7>>\)

Пример 3

Далеко не всегда часть числа делится на числитель данной дроби; в таких случаях мы будем получать в ответе не целые числа, а дроби или смешанные числа.

\(\mathbf<\frac<2><3>>\) от числа равны 11, найдите исходное число.

Во всем остальном решение ничем не будет отличаться- также разделим дробь от числа, равную \(\mathbf<\frac<2><3>>\), на величину дроби, равную 11 и получим результат.

Для получения ответа нам понадобилось выделить целую часть.

Важен еще один случай.

Никто не гарантирует, что данная нам часть числа сама по себе не будет являться дробью.

Такого случая не стоит пугаться, а стоит придерживаться алгоритма, а именно делить часть числа на то, какой дробью она является.

Пример 4

\(\mathbf<\frac<5><6>>\) от числа равны \(\mathbf<\frac<2><3>>\), найдите все число.

Для решения этого примера разделим \(\mathbf<\frac<2><3>>\)- часть числа, на \(\mathbf<\frac<5><6>>\)- дробь.

Все исходное число равняется \(\mathbf<\frac<4><5>>\)

Пройти тест и получить оценку можно после входа или регистрации

Нахождение числа по проценту

Теперь представим, что дан какой-то определенный процент от числа и необходимо найти, от какого числа брали процент.

Вспомним, что процент- это способ записи десятичной дроби.

То есть, чтобы из процента получить десятичную дробь, которую он обозначает, надо величину процента разделить на 100.

Поэтому для решения такого рода задач надо преобразовать процент в десятичную дробь, а дальше сделать все то же самое: разделить число на эту дробь.

Пример 1

Известно, что зарплата работника увеличилась на 2 000 рублей или на 25 процентов. Какая зарплата у работника была изначально?

Решение:

Переведем проценты в дроби: \(\mathbf<25\%=25\div100=0.25>\)

Разделим число на дробь: \(\mathbf<2000\div0.25=8000>\)

Ответ: изначально зарплата работника была 8000 рублей.

Чтобы найти число по проценту от него, надо перевести процент в десятичную дробь, а после разделить данную часть числа на полученную дробь.

Пример 2

Сказано, что 9% от числа равны 81. Необходимо найти все число.

Решение:

Первым действием переводим проценты в десятичную дробь.

Вторым действием делим данное число на эту дробь.

Ответ: искомое число 900

Пройти тест и получить оценку можно после входа или регистрации

Решение задач на дроби от числа и проценты

Задачи, в которых фигурируют дроби от числа часто встречаются не только в школьных учебниках и задачниках, но и в реальной жизни, поэтому стоит уделить им особое внимание.

Сначала разберем некоторые из таких задач вместе, а дальше вы попробуете свои силы в самостоятельном решении задач.

Часть задач тривиальна, иными словами, их решение очевидно, достаточно лишь увидеть в них формулу, подставить в нее данные значения и получить результат.

Пример:

Айсберг возвышается над водой на \(\mathbf<\frac<1><11>>\) своей высоты.

Капитан корабля заметил, что от воды до макушки айсберга по вертикали 16 метров.

Какова общая высота айсберга?

Решение:

В данном случае мы сразу можем сказать, что все число- это общая высота айсберга, дробь от числа- 16 (метров), а величина дроби- \(\mathbf<\frac<1><11>>\).

Соответственно, по правилу, для получения ответа мы делим 16 на \(\mathbf<\frac<1><11>>\) и получаем результат.

\(\mathbf<16\div\frac<1><11>=16\cdot11=176>\) (метр)- общая высота айсберга

Ответ: 176 (метров).

Некоторые задачи для своего решения требуют более глубокого анализа.

Пример:

Магазин продал \(\mathbf<\frac<2><3>>\) пар новых кроссовок специальной партии, после чего на складе осталось 56 пар.

Какого размера была специальная партия?

Решение:

В данной задаче, если не вчитываться в условие, интуитивно хочется просто поделить 56 на \(\mathbf<\frac<2><3>>\) и получить ответ, но ответ не будет правильным.

Если посмотреть внимательно, то 56 пар соответствуют оставшейся части партии, в то время как дробь \(\mathbf<\frac<2><3>>\) описывает проданную часть.

Но мы пока не знаем общего количества пар и не можем сказать, какому числу соответствует \(\mathbf<\frac<2><3>>\)

Зато мы можем вычислить размер оставшейся части.

Если вся партия — это 1, и продано \(\mathbf<\frac<2><3>>\), значит осталась \(\mathbf<\frac<1><3>>\) товара.

Эта дробь соответствует 56 оставшимся парам.

Дальнейшие действия аналогичны рассмотренным в предыдущей задаче.

Теперь оформим решение:

1) \(\mathbf<1-\frac<2><3>=\frac<1><3>>\) составляет оставшаяся часть от всего размера партии

2) \(\mathbf<56\div\frac<1><3>=56\cdot3=168>\) (пар) кроссовок всего было в партии

Ответ: 168 (пар).

Вам могут встретиться задачи и с более сложными условиями, все их разобрать невозможно, но главное:

• не давать себя запутать
• расписать, какой части какая дробь и какое число соответствует
• понять, где данных достаточно, чтобы узнать что- то новое
• и так постепенно продвигаться к ответу

Пройти тест и получить оценку можно после входа или регистрации

Интересная информация

Задачи математики часто диктуются другими науками, в том числе экономикой.

Существуют поднауки других наук, связанные с математикой. Примерами таких могут служить математическая физика, изучающая, как следует из названия, физические модели, а также математическая экономика, о которой мы вам сейчас расскажем.

Предметом изучения этой теории является математическое описание экономических объектов, явлений и процессов.

В самом деле, интересно применить мощнейший математический аппарат к таким насущным вопросам, как изменение цен и доходов, изменение предпочтений покупателей и пр.

Истоки математической экономики идут с XVII века. Тогда преподаватели германских университетов начали использовать новый стиль преподавания, который включал в себя статистику. Там, где появляется статистика, то есть множество чисел, появляется и математика, которая выявляет какие-то закономерности.

К примеру, расчет среднего дохода крестьян не является сложной задачей и сводится к вычислению среднего арифметического, но тоже является задачей математики.

В это же время группа английских ученых создала метод «численной аргументации государственной политики», который затрагивал темы налогов, сборов, таможенных пошлин, и прочие экономические процессы, в которых участвует государство.

К XIX веку появляется и развивается классическая школа политической экономики, чьим лицом принято считать Адама Смита.

Именно в этот период математика начала активно применяться в экономике.

В дальнейшем все большее количество математических инструментов переходило в экономику, а в наши дни на нее трудятся еще и информационные технологии.

Так что в наши дни великим экономистом может быть не тот, кто изначально учился на экономиста, а успешный математик или программист.

Заключительный тест

Пройти тест и получить оценку можно после входа или регистрации

Источник