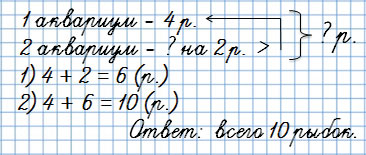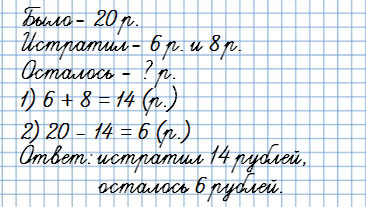Как написать задачу разными способами

Различные способы решения задач и различные формы записи решения

Страницы работы

Содержание работы

С. Е. ЦАРЕВА. Различные способы решения задач и различные формы записи решения// Начальная школа, 1982. — №2. – с.39-41.

На одном из уроков математики во II клас­се ученик, получив задание “Реши задачу”, спросил: “Каким способом нужно решать: по действиям или выражением”. Учитель ответил: “По действиям”.

Этот диалог показал, что и учитель, и уче­ник принимают различные формы запи­си решения за различные способы ее решения. Посещение уроков, беседы с учителями и учащимися позволили нам сде­лать вывод, что эта ошибка довольно распро­странена. Смешение же названных понятий приводит к тому, что, когда требуется дей­ствительно решить задачу разными способами, учащиеся либо вовсе не понимают задания, либо понимают его с большим трудом. А это, в свою очередь, снижает обучающие и воспитывающие возможности такого важного вида работы над задачей, как решение задач раз­ными способами.

Поэтому мы считаем своевременным обра­тить внимание учителей на отличие понятий способа решения задачи и формы записи решения задачи.

Задача считается решенной различными спо­собами, если се решения отличаются связями между данными и искомыми, положенными в основу решений, или последовательностью использования этих связей.

Рассмотрим, например, задачу № 522 из учебника математики для II класса: “Для уро­ков труда купили 4 катушки белых ниток, по 10 коп. за катушку, и 6 катушек черных ни­ток по такой же цене. Сколько денег уплатили за эти нитки?”

Эта задача может быть решена двумя ариф­метическими способами.

При первом из них, наиболее очевидном, первоначально определяют стоимость черных ниток: (10-4)-коп., затем стоимость белых ни­ток: (10-6) коп. и, наконец, стоимость всех ниток.

При втором способе замечаем, что цена 1 катушки белых ниток та же, что и черных, поэтому вначале можно узнать, сколько всего катушек ниток купили (6+4), а затем опре­делить стоимость всех этих ниток

Запись решения, для каждого способа может быть выполнена в нескольких формах. Пока­жем все эти формы для каждого способа ре­шения.

Запись решения по действиям с пла­ном.

1. Сколько стоят белые нитки? 10·4 = 40 (коп.)

2. Сколько стоят черные нитки? 10·6=60 (коп.)

3. Сколько денег уплатили за все эти нитки?

1. Сколько всего катушек с нитками купили?

2. Сколько денег уплатили за все эти нитки?

В настоящее время эта форма записи реше­ния задач в начальной школе практически не применяется. Однако мы считаем, что озна­комить с ней учащихся полезно и ее можно использовать на уроках математики, хотя и значительно реже, чем другие формы.

Рассмотрим другую форму записи решения той же задачи — это запись решения по дей­ствиям с пояснениями.

1. 10 · 4 =40 (коп) — стоимость белых ниток,

2. 10 ·6 = 60 (коп) — стоимость черных ни­ток.

3. 40+60=100 (коп.) — стоимость всех ни­ток.

4. 100 коп.= 1 руб.

1. 6+4 = 10 (шт.) — всего купили катушек ниток.

2. 10·10 = 100 (коп) — стоимость всех ниток.

3. 100 коп. = 1 руб.

Решение задачи можно также оформить по действиям без пояснений.

3. 40 + 60=100 (коп).

4. 100 коп. = 1 руб.

2. 10 · 10=100 (коп).

3. 100 коп.= 1 руб.

Ответ: все нитки стоят 1 руб.

Ответ: все нитки стоят 1 руб.

По задаче можно также составить выражение и найти его значение.

10 · 4+10 · 6=100 (коп)

Ответ: все нитки стоят 1 руб

Ответ: все нитки стоят 1 руб.

Запись решения в этой форме осуществляется учащимися в два этапа. Вначале составляется выражение, затем учащиеся находят его значение, после чего запись решения приобретает вид равенства, в левой части кото­рого записано выражение, составленное по задаче, а в правой части — его значение.

Ни в коем случае нельзя называть запись 10 · 4 + 10 · 6 = 100 выражением, так как это противоречит тому определению поня­тия выражения, которое положено в основу изучения этого понятия в школе. Математи­ческое выражение составляется из цифр, букв, знаков арифметических действий и скобок, но не содержит знаков математических отноше­ний: равенства, неравенства и др. Два мате­матических выражения, соединенные знаком равенства, образуют равенство.

Приведенная выше запись — это равенство, левая часть которого есть выражение, составленное по задаче (10 · 4 + 10 ··6), а правая часть — выражение, состоящее всего лишь из одного числа (100), являющегося значением предыдущего выражения.

При проверке решения задачи, записанной в этой форме, учащимся можно дать такие задания:

1. Прочитайте выражение, составленное по задаче.

При выполнении этого задания учащиеся должны прочитать только левую часть равен­ства. (Сумма двух произведений 10·4 и 10·6.) После чтения выражения можно задать вопро­сы, ответы на которые покажут, как учащие­ся понимают смысл каждой части выражения (10 — 4 и 10 — 6) и всего выражения в целом (10 · 4 +10 · 6): что означает произведение деся­ти и четырех? десяти и шести? что означает сумма этих произведений?

2. Назовите значение этого выражения. (Значение составленного по задаче выражения равно 100.)

3. Дайте ответ на вопрос задачи. (Все нитки стоят 100 коп., т. е. 1 руб.)

При решении задач следует правильно употреблять в своей речи соответствующие термины: Решите задачу и запишите решение по действиям с пояснениями. Решите задачу двумя способами, записав каждое решение в виде равенства, левая часть которого — выражение, составленное по задаче. Решите задачу двумя способами. Составьте соответствующие выражения и найдите их значения. Решите задачу и запишите решение вначале по действиям с пояснениями, а затем в виде выражения. Найдите значение этого выражения. Дайте ответ на вопрос задачи.

Источник

Способы записи решения задач.
учебно-методический материал по математике

Учебный-методический материал поможет учителю при работе с текстовыми задачами на уроках математики.

Скачать:

Вложение	Размер
sposoby_zapisi_resheniya_zadach.doc	26 КБ

Предварительный просмотр:

Способы записи решения задач.

Начальный курс математики ставит своей основной целью научить младших школьников решать задачи арифметическим способом, который сводится к выбору арифметических действий, моделирующих связи между данными и искомыми величинами. Решение задач в этом случае оформляется в виде последовательности числовых равенств, к которым даются пояснения, или числовым выражением. В начальных классах используются различные формы записи решения задач арифметическим способом: по действиям; по действиям с пояснением; с вопросами; выражением.

У мальчика было 90 книг. 28 он поставил на первую полку. 12 — на вторую, остальные — на третью. Сколько книг на третьей полке?

а ) Решение по действиям:

Ответ: 50 книг на третьей полке.

б ) По действиям с пояснением:

1) 28+12=40 ( к.) — на первой и второй полках вместе,

2) 90-40=50 ( к.) — на третьей полке.

1) Сколько книг на первой и второй полках вместе?

2) Сколько книг на третьей полке?

Ответ: 50 книг на третьей полке,

При записи решения задачи выражением можно вычислить его значение. Тогда запись решения задачи будет выглядеть так: 90-(28+12)=50 (к.)

Ответ: 50 книг на третьей полке.

Не следует путать такие понятия, как: решение задачи различными способами (практический, арифметический, графический, алгебраический); различные формы записи арифметического способа решения задачи (по действиям, выражением, по действиям с пояснением, с вопросами) и решение задачи различными арифметическими способами. В последнем случае речь идет о возможности установления различных связей между данными и искомыми, а следовательно, о выборе других действий или другой их последовательности для ответа на вопрос задачи.

Например, рассмотренную выше задачу можно решить другим арифметическим способом:

1) 90-28 = 62 ( к.) — на второй и третьей полке,

2) 62-12 = 50 ( к.) — на третьей полке.

Ответ: 50 книг на третьей полке.

В качестве арифметического способа можно рассматривать и такое решение

1) 90-12 = 78 ( к.) — на первой и третьей полке,

2) 78-28 = 50 ( к.) — на третьей полке.

Ответ: 50 книг на третьей полке

По теме: методические разработки, презентации и конспекты

Урок математики во 2 классе «Решение задач графическим способом»

Урок развивает умение решать текстовые задачи графическим способом; развивает математическую речь, логическое мышление; воспитывает интерес к точным наукам, аккуратность, чувство товарищества, в.

Конспект урока русского языка на тему: «Выявление орфографической задачи на месте сочетаний [сн], [с\’н\’] и способы её решения.

Тема урока: «Выявление орфографической задачи на месте сочетаний [сн], ]с\’н\’] и способы её решения»Цель урока: усвоение основ орфограммНа уроке ребята узнают, что некоторые звуки руссого языка трудно .

Мастер-класс » Комбинаторные задачи и способы их решения»

ФГОС второго поколения начального общего образования определяет новые требования к уровню подготовки младших школьников, что предполагает необходимость переосмысления учителями начальной школы как сам.

Конспект урока математики по теме: «Решение задач разными способами»

Конспект урока с использованием деятельностного подхода.

Конспект урока по математике в 3 классе «Решение задач разными способами»

Конспект урока по математике в 3 классе.

Методика записи краткого условия и решения задачи.

Уроки счета для глубоко умственно отсталых связаны с формированием разнообразных умений и навыков умственной и учебной деятельности способствуют коррекции недостатков познавательной деятельности и лич.

Конспект урока математики 4 класс (система Д.Б.Эльконина – В.В.Давыдова) Тема. Анализ средств для самоконтроля при составлении краткой записи и решении задач.

Конспект урока математики 4 класс (система Д.Б.Эльконина – В.В.Давыдова)Тема. Анализ средств для самоконтроля при составлении краткой записи и решении задач.Тип урока. Урок рефлексии.Цель. Форми.

Источник

Образцы оформления задачи

В разделе «Задачи» мы рассмотрели несколько видов задач. Теперь поучимся оформлять решения к ним.

В вопросе задач такого типа всегда есть «Сколько всего?»

На школьном участке ребята посадили 7 лип и 4 клёна.

Сколько всего деревьев посадили ребята?

2. Задачи на нахождение остатка

В вопросе «Сколько . осталось?»

Мама с Юлей посадили 7 кустов смородины. Затем они полили 4 куста.

Сколько кустов смородины осталось полить?

В условии «на . больше»

Папа с Володей собирали грибы. Папа нашёл 8 грибов, а Володя на 3 гриба больше.

Сколько грибов нашёл Володя?

В условии «на . меньше»

У Ани было 10 рублей, а у Оли на 2 рубля меньше.

Сколько денег было у Оли?

4. Задачи на разностное сравнение

Краски стоят 15 рублей, а альбом 8 рублей.

На сколько рублей краски дороже альбома?

«На сколько меньше. «

Дыня весит 3 кг, а арбуз 7 кг.

На сколько кг дыня легче арбуза?

5. Задачи на нахождение неизвестного слагаемого

В условии «Было. Стало. «

В вопросе «Сколько добавили?»

У Саши было 4 карандаша. Когда ему купили еще несколько карандашей, у него их стало 9.

Сколько карандашей купили Саше?

6. Задачи на нахождение неизвестного вычитаемого

В условии «Было. Осталось. «

В вопросе «Сколько уехало?»

«Сколько человек вышло?»

В гараже было 9 машин. Когда несколько машин уехало, в гараже осталось 5 машин.

Сколько машин уехало?

7. Задачи на нахождение неизвестного уменьшаемого

В условии «Убрали. Осталось. «

В вопросе «Сколько было сначала?»

После того, как Дима отдал 2 свои машинки младшему брату, у него осталось 6 машинок.

Сколько машинок было у Димы сначала?

Задачи в 2 и 3 действия

Бабушка испекла пончики и разложила их по тарелкам. На первую тарелку она положила 5 пончиков, а на вторую на вторую на 2 пончика меньше.

Сколько всего пончиков испекла бабушка?

В классе два маленьких аквариума. В первом аквариуме 4 рыбки, а во втором — на 2 рыбки больше.

Сколько рыбок в двух аквариумах?

У Тани было 10 тетрадей. Она использовала 4 тетради.

На сколько больше тетрадей осталось, чем Таня использовала?

У Юры было 12 счетных палочек. Для решения примеров он использовал сначала 3, а потом еще 4 палочки.

Сколько палочек у него осталось?

У Вани было 20 рублей. На покупку карандаша и ручки он истратил 6 и 8 рублей.

Сколько рублей осталось у Вани?

Задачи с составлением таблиц по из условию:

I тип:

На 3 одинаковые шторы израсходовали 18 м ткани. Сколько таких штор можно сшить из 30 м такой же ткани?

В двух одинаковых пакетах 4 кг муки. Сколько килограммов муки в пяти таких пакетах?

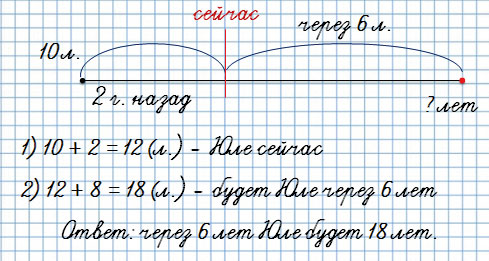
Задачи с составлением рисунка по условию:

Два года назад Юле было 10 лет. Сколько лет будет Юле через 6 лет?

Поделись с друзьями в социальных сетях:

Источник