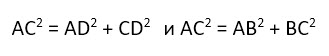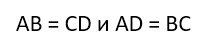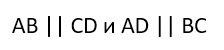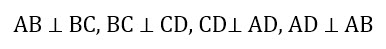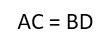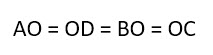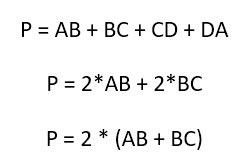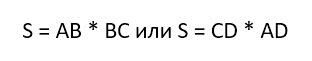Как можно назвать прямоугольник 2 способом

Прямоугольник — это одна из основ геометрии

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.

Сегодня мы расскажем об одной из основных геометрических фигур – ПРЯМОУГОЛЬНИКЕ.

Название это весьма говорящее, и в нем скрыто официальное определение.

Прямоугольник – это четырехугольник, у которого все углы прямые, то есть равны 90 градусам.

Впервые описание этой фигуры встречается еще в Древнем Египте. Но в те времена все геометрические правила давались как неопровержимые истины, не предоставляя доказательств.

Более правильный подход появился в Древней Греции. И естественно, автором стал самый знаменитый математик той эпохи — Евклид. А прямоугольник, как и многие другие фигуры и термины, был подробно описан в его произведении «Начала».

Прямоугольник — это.

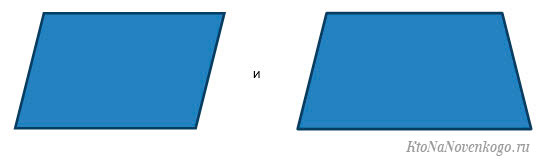
Все тот же Евклид разделил все четырехугольники на два вида – параллелограммы (что это?) и трапеции (что это?).

У первых противоположные стороны равны и параллельны, а у вторых параллельна только одна пара сторон, и они при этом не равны.

То есть выглядит это так:

Так вот, прямоугольник в данном случае является частным случаем параллелограмма.

У этой фигуры противоположные стороны параллельны. Это первое условие по Евклиду. И к тому же они равны, что является условием номер два.

У прямоугольника есть и собственный частный случай. Когда равны не только противоположные стороны, а все. И как нетрудно догадаться, фигура эта называется квадрат.

Ну, и логично предположить, что квадрат (как и сам прямоугольник) является частным случаем параллелограмма.

Признаки прямоугольника

Признаки геометрической фигуры – это совокупность отличий, по которым ее можно выделить среди других.

В случае с прямоугольником их всего три:

1. Если один из углов параллелограмма прямой, то данный параллелограмм является прямоугольником.
2. Если три угла четырехугольника являются прямыми, то перед нами опять же прямоугольник. При этом нет необходимости доказывать, что четырехугольник является параллелограммом. Это промежуточное звено становится верно само по себе.
3. Если диагонали параллелограмма равны между собой, то фигура точно является прямоугольником.

» alt=»»>

Диагонали прямоугольника

Как мы уже упомянули выше, диагонали прямоугольника (отрезки, соединяющие его противоположные углы) равны между собой.

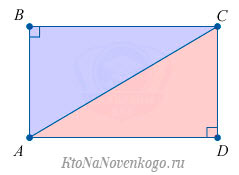
Доказать это можно с помощью известной теоремы Пифагора. Она гласит, что «Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы».

В нашем случае гипотенузой является диагональ прямоугольника, которая делит его на два равных прямоугольных треугольника. И теорема Пифагора выглядит следующим образом:

Свойства прямоугольника

К свойствам прямоугольника относятся следующие утверждения:

Прямоугольник является параллелограммом, а значит имеет все присущие ему свойства.
У прямоугольника равны противоположные стороны.





















Периметр и площадь

Для того чтобы определить периметр прямоугольника, надо просто сложить длины всех его четырех сторон.



Но с учетом того, что попарно они равны, то конечная формула может выглядеть более просто:



Площадь прямоугольника вычисляется также весьма просто. Надо лишь перемножить две его стороны:



К слову, это не единственная формула для вычисления площади. Площадь также можно получить, имея значение периметра фигуры или длину его диагонали. Но эти формулы гораздо сложнее.



Вот и все, что мы хотели рассказать о геометрической фигуре ПРЯМОУГОЛЬНИК. До новых встреч на страницах нашего блога.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (5)

Главная основа геометрии — это все же треугольник. Через него можно построить любую фигуру и доказать любую теорему.

Прямоугольник отличается от квадрата, этому учат в школе в младших классах. Квадрат — это одинаковая длина соединяющих углов, если я правильно выражаюсь, а прямоугольник формы может быть: телефон, звуковые колонки, паспорт и прочее.

Не согласен с утверждением, что раз один угол прямой, то перед нами точно прямоугольник, всё же прямоугольник — это когда все противоположные стороны параллельны друг другу, а если только один угол прямой, то там и трапеция может быть.

Я бы сказала, что прямоугольник — это основа архитектуры. Все здания так или иначе используют эту фигуру в своем дизайне.

Вот за что я люблю прямоугольники, так за то, что площадь его легко найти, да и периметр, вот с трапецией сложнее, увы, но те же земельные участки больше трапеции, отсюда и земельные споры.

Источник

Урок геометрии во 2-м классе по теме: «Виды четырехугольников. Прямоугольник»

Тема: Виды четырехугольников. Прямоугольник

Цели:

1. Обеспечить усвоение учащимися знаний о различных видах четырехугольников, прямоугольника.
2. Развить умения классифицировать факты, делать выводы, строить прямоугольник и отличать его из ряда четырехугольников.
3. Воспитание мотивов учения, положительного отношения к занятиям.

Тип урока – комбинированный.

Вид урока – дидактическая игра.

Методы и приемы обучения: диалогический и эвристический методы:

• организация труда в парах;
• фронтальная работа;
• оперативная форма проверки знаний (спецкарточки);
• демонстрация наглядных пособий;
• работа в бригадах.
• кодоскоп;
• плакат с видами четырехугольников;
• наглядные пособия к сказке;
• сигнальные карточки;
• перфокарты для каждого ученика с заготовленными таблицами;
• заготовки прямоугольников;
• ножницы, линейки, карандаши, чертежные треугольники;
• магнитная доска;
• прямоугольники с номерками;
• раздаточный материал (прямоугольники красного цвета для поощрения отвечающих);
• магнитофон.

Ход урока

Сегодня на уроке мы с вами совершим путешествие в удивительную страну Геометрию:

– Кто знает, что в переводе с греческого обозначает слово “геометрия”?

“Гео” – земля, “метрия” – измерение.

Наука эта появилась в Греции.

Сопровождать нас будет в нашем путешествии (учитель показывает сказочного героя) удивительный герой – волшебник.

– Всех вас он зашифровал, и вы будете путешествовать под зашифрованными номерами.

– Кто узнал его? (Старик Хоттабыч.)

– Кто написал книжку “Старик Хоттабыч”? (Лагин.)

Старик Хоттабыч очень старый волшебник и его знания устарели, поэтому он пришел к вам на урок и хочет узнать, что же сейчас изучают современные дети. Помогите волшебнику разобраться.

– Что изображено на доске? (Геометрические фигуры.)



– Определите на какие 2 группы вы могли бы разделить эти геометрические фигуры? (Треугольники и четырехугольники.)

Заполните карточку №1. Укажите номера треугольников и четырехугольников. Все дети указывают в карточке номера.

Каточка №1

1 3 5 7 9 10

В это время 2 ученика фиксируют ответы на доске.

– Укажите во второй карточке номера треугольников по углам (тупоугольный, прямоугольный, остроугольный) и по сторонам (равносторонний и равнобедренный).

Работу выполняют по вариантам, а потом обмениваются карточками и осуществляют взаимопроверку в парах.

Углы треугольника

ников Тупоугольный

Остроугольный 5 7

1 10 Вариант №1: Карточка №2

Стороны треугольника

ников Равносторонний

Равнобедренный 10

1) Сегодня мы с нашим героем познакомимся с видами четырёхугольников, а именно; с прямоугольником, научимся его чертить и выделять среди других фигур Т.к. треугольников и четырёхугольников в геометрии много. Вот как выглядят некоторые из них:



– Какие из них вы уже знаете?

Дети называют те виды, которые знают.

– Что общего у этих фигур, что их объединяет в одну группу?

(4 стороны, 4 угла, 4 вершины.)

– А чем один вид отличается от другого? (Длинами сторон и особенностями углов.)

Учитель обращает внимание детей на таблицу и говорит определения.

1. Квадрат – прямоугольник, у которого все стороны равны.
2. Трапеция – четырехугольник, у которого только 2 противоположные стороны параллельны (перевод “столик”).
3. Параллелограмм– четырехугольник, у которого противоположные стороны параллельны и равны.
4. Ромб– параллелограмм, у которого все стороны равны.
5. Неправильный четырехугольник– фигура, у которой стороны не равны и не параллельны.

2) Помогите Хоттабычу из ряда четырехугольников найти похожие (1 3 5).



– Как называются углы у фигур 1, 3, 5? (Прямые.)

– А как бы вы назвали эти фигуры? (Прямоугольники.)

– Попробуйте сказать, что же такое прямоугольник?

Прямоугольник – геометрическая фигура, у которой все углы прямые и противоположные стороны равны.

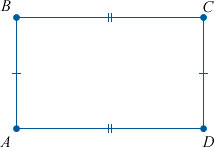
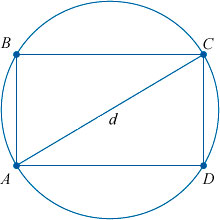
– Назовите вершины у прямоугольника АВСД? (А, В, С, Д – вершины.)

Источник

Что такое прямоугольник: определение, свойства, признаки, формулы

В данной публикации мы рассмотрим определение, свойства и признаки одной из основных геометрических фигур – прямоугольника. Также приведем формулы, с помощью которых можно найти его площадь и периметр.

Определение прямоугольника

Прямоугольник – это четырехугольник, у которого все углы равны 90° (т.е. являются прямыми).



∠ABC = ∠BCD = ∠BAD = ADC = 90°

Прямоугольник состоит из:

• длины – более длинная пара сторон. Обычно обозначаются латинской буквой, например, a;
• ширины – более короткая пара сторон. Чаще всего обозначаются как b.

Сам прямоугольник обычно записывается путем перечисления его вершин, например, ABCD в нашем случае.

Примечание: Прямоугольник является разновидностью параллелограмма.

Свойства прямоугольника

Свойство 1

Противоположные стороны прямоугольника попарно параллельны и равны.



Свойство 2

Длина и ширина прямоугольника одновременно являются его высотами, т.к. они взаимно перпендикулярны.



• a– это высота h₁, проведенная к стороне b
• b– это высота h₂, проведенная к стороне a

Свойство 3

Если соединить середины сторон прямоугольника, то получится ромб.



Свойство 4

Квадрат диагонали (d) прямоугольника равняется сумме квадратов его смежных сторон.

d 2 = a 2 + b 2



Это следует из теоремы Пифагора, которую можно применить к любому из прямоугольных треугольников, которые образуются в результате деления диагональю прямоугольника.

Свойство 5

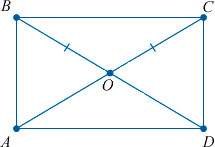
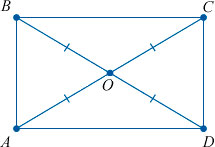
Диагонали прямоугольника равны, и в точке пересечения делятся пополам.



Свойство 6

Около любого прямоугольника можно описать окружность, радиус (R) которой равен половине диагонали этого прямоугольника.



Следовательно, диаметр окружности равен полной длине диагонали прямоугольника.

Признаки прямоугольника

Параллелограмм является прямоугольником, если верно одно из следующих утверждений:

• Его диагонали равны.
• Все его углы равны.
• Если квадрат диагонали равен сумме квадратов его смежных сторон.

Формулы

1. Площадь прямоугольника (S):

2. Периметр прямоугольника (P):

Источник

Читайте также:  Лапша удон dr naturi способ приготовления