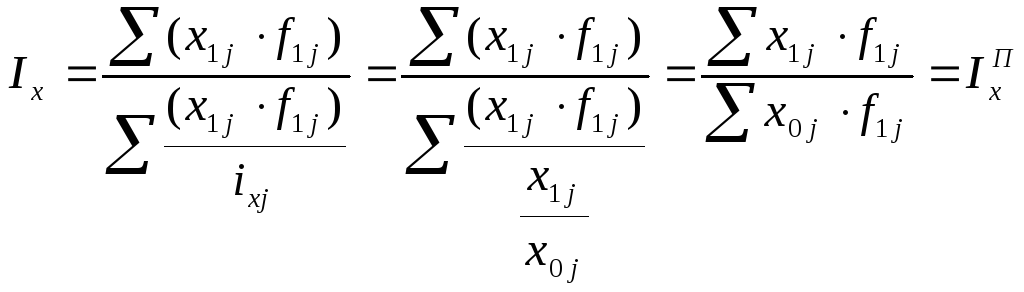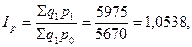Как классифицируются индексы по способу построения агрегатные

48. Агрегатные индексы и их виды

Агрегатный индекс является основной формой индекса.

Он строится как отношение сумм произведений двух величин: 1) индексируемой величины; 2) показателя-соизмерителя (веса индекса).

Формула агрегатного индекса в общем виде имеет следующий вид:

,

где х_1j – сравниваемое (текущее) значение индексируемой величины j-го элемента;

х_0j – базисное значение индексируемой величины j-го элемента;

f_j – показатель-соизмеритель (вес индекса) для j-го элемента;

– результативный показатель для j-гo элемента;

J – всего элементов в совокупности.

В зависимости от того, какому уровню (базисному или текущему) относится вес индекса различают 2 вида агрегатных индекса:

Агрегатный индекс Ласпейреса: (базисный)

Агрегатный индекс Пааше: (текущий)

Индексы физического объема:

Агрегатный индекс цен:

49. Средние индексы на основе индивидуальных индексов

Сводный индекс может быть построен как среднее взвешенное арифметическое или гармоническое из индивидуальных индексов.

При этом значение среднего индекса должно совпадать со значением агрегатного индекса (Ласпейреса или Пааше). Весами усреднения выступают результативные показатели (либо базисного, либо текущего уровня).

Метод усреднения зависит от имеющейся в распоряжении информации.

1) Если имеются данные об индивидуальных индексах (i_xj) и о значении результативного показателя базисного уровня (), то сводный индекс рассчитываем как среднее арифметическое взвешенное с весами, равными данному результативному показателю.

2) Если имеются данные об индивидуальных индексах (i_xj) и о значении результативного показателя текущего уровня – (), то сводный индекс рассчитываем как среднее гармоническое взвешенное с весами, равными данному результативному показателю.

50. Индексный метод анализа факторов

Некоторые социально-экономические показатели находятся между собой в определенной (функциональной) связи, например, в виде произведения (либо отношения). В таком же соотношении должны находиться и статистические показатели, характеризующие изменение исходных социально-экономических показателей (т. е. индексы).

Если , то.

Данное соотношение между индексами осуществимо, если веса индексирования для I_X и I_Y берутся за разные периоды времени (или относятся к разным объектам), т. е. один из индексов должен быть построен по формуле Ласпейреса, а другой – по формуле Пааше:

.

Индексный метод позволяет также представить абсолютное изменение результативного показателя () как результат влияния различных факторов (входящих в формулу его расчета).

Общее абсолютное изменение результативного показателя текущего уровня по сравнению с базисным определяется как разница между числителем и знаменателем в формуле сводного индекса данного результативного показателя:

.

Оно может быть разложено на составляющие: абсолютные изменения за счет отдельных факторов, входящих в его расчетную формулу (,).

51. Взаимосвязь между индексами переменного, постоянного состава и структурных сдвигов.

Индексы позволяют анализировать изменения не только агрегатов, но и их средних величин с помощью индексов переменного и постоянного состава и структурного сдвига. Если индексируемую величину обозначить через X, а веса усреднения – через f, то индекс средней величины можно записать так:

.

Данный индекс называют еще индексом переменного состава (I_пс)

Если при расчете индекса средних величин использовать веса усреднения одного и того же уровня (либо текущего – f₁, либо базисного – f₀), то влияние изменения структурного фактора на изменение средней величины будет устранено. Такой индекс называют индексом фиксированного (постоянного) состава – I_фс:

.

Если при расчете индекса средних величин использовать значения усредняемого признака X одного и того же уровня (либо текущего – Х₁, либо базисного – Х₀), то на изменение средних будет оказывать влияние только изменение весов, т. е. структуры совокупности. Этот индекс условно называют индексом структуры (или индексом структурного сдвига):

.

Индекс структуры показывает, в какой степени изменение средней величины индексируемого показателя произошло за счет изменения структуры (состава) совокупности.

Между индексами переменного, постоянного состава и структурных сдвигов существует следующая взаимосвязь:

.

Источник

ВИДЫ ИНДЕКСОВ, СПОСОБЫ ИХ ПОСТРОЕНИЯ

Лекция No 9: «ИНДЕКСНЫЙ МЕТОД АНАЛИЗА»

Учебные вопросы лекции:

1. Понятие об индексах и их значение в анализе

2. Виды индексов, способы их построения

3. Индексы Ласпейреса, Пааше, Фишера. Взаимосвязи важнейших

ПОНЯТИЕ ОБ ИНДЕКСАХ И ИХ ЗНАЧЕНИЕ В АНАЛИЗЕ

Для всесторонней характеристики сложных массовых явлений и

анализа роли факторов на изменение результативных показателей

используют систему индексов.

В практике статистики индексы наряду со средними величинами

являются наиболее распространенными статистическими показателями. С их

помощью характеризуется развитие национальной экономики в целом и ее

отдельных отраслей, анализируются результаты производственно-

хозяйственной деятельности предприятий и организаций, исследуется роль

отдельных факторов в формировании важнейших экономических

показателей, выявляются резервы производства, индексы используются

также в международных сопоставлениях экономических показателей,

определении уровня жизни, мониторинге деловой активности в экономике.

В статистике под индексом понимается обобщающий относительный

показатель, характеризующий среднее изменение массовых общественных

явлений во времени и пространстве, состоящих из непосредственно

Индексируемая величина – это показатель, изменение которого

характеризует индекс. Она устанавливается исходя из названия индекса.

Коэффициент соизмерения или соизмеритель – это величина,

приводящая непосредственно несоизмеримые элементы к сопоставимому

Индексы позволяют решать в экономическом анализе следующие

✓ дают обобщенную количественную характеристику уровня

плановых заданий, оценивают степень выполнения плана по группе

разнородных предприятий, отраслей;

✓ отражают изменение сложных массовых явлений в динамике;

✓ устанавливают меру различий в уровнях сложных массовых

явлений в пространстве;

✓ определяют меру влияния отдельных факторов на изменение

✓ устанавливают влияние структурных сдвигов на изменение

ВИДЫ ИНДЕКСОВ, СПОСОБЫ ИХ ПОСТРОЕНИЯ

Индексы классифицируются по следующим принципам:

1. по степени охвата явлений;

2. по базе сравнения;

3. по виду весов (соизмерителей);

4. по форме построения;

5. по составу явлений;

6. по содержанию индексируемых величин;

7. по объекту исследования;

8. по периоду исчисления.

I. По степени охвата совокупности индексы бывают:

(1) Индивидуальные индексы дают относительную характеристику

изменения отдельных элементов сложных массовых явлений и получаются в

результате сравнения однотипных явлений. В зависимости от

экономического назначения индивидуальные индексы бывают: физического

объема продукции, себестоимости, цен и т. д.:

(2) Групповые индексы используются для характеристики изменения

части или группы элементов, имеющих определенную качественную

общность, но непосредственно несоизмеримых.

(3) . Общие индексы характеризуют изменение сложного массового

явления, составные части которого непосредственно несоизмеримы. Общие

индексы состоят из количественных (объемных) и качественных показателей.

В экономических расчетах чаще всего используются общие индексы.

Индивидуальные индексы принято обозначать i, а общие индексы – I.

II. По базе сравнения индексы могут быть

— динамические индексы отражают изменение явления во времени. При

исчислении этих индексов сравнивают значения показателя за отчетный

период со значением этого показателя за предыдущий период, который

называют базисным. Они бывают двух видов: базисные и цепные индексы:

Источник

Агрегатные индексы. Построение взаимосвязанных агрегатных индексов

Общие индексы по форме построения могут быть агрегатными и средними.

Агрегатные индексы – это индексы, в которых числитель и знаменатель представляют собой сумму произведений показателей (т.е. агрегат). Как правило, перемножаются два показателя: один из них – индексируемая величина, а второй – ее вес.

Агрегатная форма индекса является основной, наиболее распространенной формой индекса в экономических исследованиях.

Агрегатный способ построения индексов позволяет с помощью определенных соизмерителей получить итоговое (суммарное) значение несопоставимых единиц сложной совокупности и в последующем сопоставить эти суммы в отчетном и базисном периодах (см. пример, таблица 9.1).

Наиболее типичные представители агрегатных индексов – индексы физического объема и цен, а также индекс стоимости. В тех случаях, когда имеются данные о производстве (о продаже) различных несоизмеримых в физических единицах продуктов в одной и той же совокупности за 2 периода и необходимо охарактеризовать изменение всего объема продуктов, они с помощью определенных соизмерителей (цены, себестоимости, трудоёмкости и т.п.) выражаются в одинаковых единицах измерения: например, q*p, q*z, q*t, и т.д. Это дает возможность соизмерить объемы продуктов в отчетном и базисном периодах:

агрегатный индекс стоимости, (9.9)

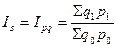
который показывает относительное изменение стоимости продуктов как за счет изменения цен, так и за счет изменения объема продуктов.

Абсолютное изменение стоимости продуктов может быть оценено как

. (9.10)

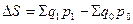
Индекс стоимости показывает, что изменение индексируемой величины обусловлено воздействием двух факторов: физического объема и цен. Для того, чтобы выявить влияние каждого из них, рассчитываются так называемые факторные индексы, которые по форме построения также являются агрегатными.

Агрегатный индекс физического объема получают путем сопоставления стоимости продукции отчетного и базисного периодов, исчисленной в неизменных ценах: ценах базисного периода:

, (9.11)

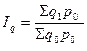
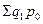
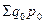
где – стоимость продукции отчетного периода в базисных ценах;

– стоимость продукции базисного периода.

Вычитая из числителя знаменатель, можно определить на сколько в абсолютном выражении изменилась стоимость продукции за счет изменения физического объема:

(9.12)

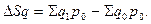
По аналогии строится и агрегатный индекс цен. Только в данном случае индексируемая величина – p, а веса – физические объемы, т.е. .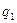

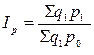
, (9.13)

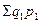
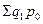
где – стоимость продукции отчетного периода;

– стоимость продукции отчетного периода в базисных ценах.

Изменение стоимости продукции за счет изменения цен в абсолютном выражении:

(9.14)

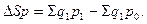
В нашем примере (таблица 9.1):

Общее изменение товарооборота:

(+12,31%)

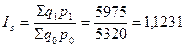
или в абсолютном выражении:

тыс. р.

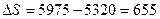
1) за счет изменения количества проданных товаров:

(+6,58%)

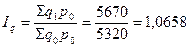
или в абсолютном выражении:

тыс. р.

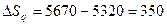
2) за счет изменения цен:

что в абсолютном выражении составит:

тыс.р.

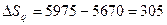
Вывод. Товарооборот в июне увеличился по сравнению с предыдущим месяцем на 12,31 %, или на 655 тыс. р. Это увеличение вызвано воздействием двух факторов: за счет роста физического объема проданных товаров – на 6,58 % (350 тыс. р.) и за счет роста цен – на 5,38 % (305 тыс. р.)

Взаимосвязь индексов 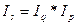носит название сопряженности индексов.

Построение системы взаимосвязанных индексов требует соблюдения следующих правил:

— веса сопряженных (факторных) индексов должны быть зафиксированы в факторных индексах на разных уровнях;

— при построении агрегатных индексов количественных величин веса (цены, себестоимость) фиксируются на базисном уровне;

— при построении агрегатных индексов качественных величин веса (физический объем) фиксируется на уровне отчетного периода.

Так, например, агрегатный индекс общих издержек:

(9.15)

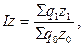
в т.ч. 1) за счет физического объема:

; (9.16)

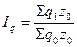
2) за счет себестоимости единицы продукции:

. (9.17)

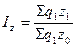
Тогда 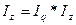– сопряженные индексы.

Свойство сопряженности используется:

а) для проверки правильности расчетов;

б) для нахождения неизвестного индекса по остальным известным, с которыми он связан как сопряженный. Например:

или .

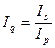
Однако на практике индексы цен и индексы физического объема могут рассчитываться и по-иному. У этого факта есть исторический аспект.

Впервые агрегатная форма индекса была предложена немецким ученым Э.Ласпейресом для измерения цен на товары. В качестве весов он предложил использовать физические объемы базисного периода.

«Индекс Ласпейреса» (9.18)

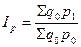
В 1874 г. другой немецкий ученый Г.Пааше предложил строить индекс цен по физическим объемам отчетного периода:

«Индекс Пааше» (9.19)

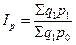
На практике могут использоваться как один, так и другой. При этом индекс Ласпейреса показывает, во сколько бы раз товары базисного периода подорожали бы (или подешевели) из-за изменения цен на них в отчетном периоде (условная экономия или перерасход).

В нашем примере:

.

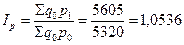
В свою очередь индекс Пааше показывает во сколько раз товары в отчетном периоде стали дороже (дешевле), чем в базисном (фактическая экономия или перерасход):

.

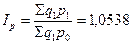
В официальной статистике исчисление индекса цен осуществляется по индексу Пааше. Он нашел наибольшее распространение и на практике, т.к. наибольший интерес для исследователя представляет фактическое изменение цен, его фактическое влияние на стоимость, а не условное изменение товарооборота или стоимости продукции.

Впоследствии названия этих разных методов (с весами базисного периода и с весами отчетного периода) были механически распространены и на другие индексы, в т.ч. и на индекс физического объема. Т.е. он может исчисляться либо по формуле

(Ласпейреса) (9.20)

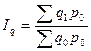
либо по формуле (Пааше). (9.21)

В первом случае I_q = 1,0658 ,

а во втором .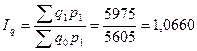

Общий подход: если в индексе использованы базисные веса – индекс построен по методу Ласпейреса;

Если в индексе использованы веса текущего периода – он построен по методу Пааше.

В начале 20 века американский экономист И.Фишер предложил в качестве формулы индекса цен среднюю геометрическую из произведения индексов Ласпейреса и Паше.

Индекс Фишера 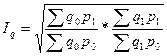. (9.22)

Его назвали идеальным. Однако он имеет недостаток: его трудно интерпретировать.

Источник