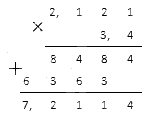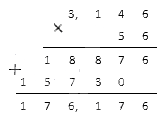Как это вычесть более рациональным способом

Приёмы рациональных вычислений.

Одно из самых важных умений человека – это умение быстро и правильно выполнять вычисления.

Рационализация вычислений означает выполнение вычислений более лёгким, более целесообразным способом.

Устные вычисления способствуют активизации мыслительной деятельности, развитию логического мышления, сообразительности, памяти, творческих начал и волевых

качеств. Способность к умственному (устному) счёту полезна

в отношении практическом и, как средство, для здоровой умственной гимнастики.

1. Приём, основанный на использовании свойств

арифметических действий.

· 89 + 67 + 11 = 89 + 11 + 67 = 167

· 357 + 996 + 48 = 357 + 996 + (43 + 4 + 1) =

= (357 + 43) + (996 + 4) + 1 = 400 + 1000 +1 = 1401

· 25 × 37 × 4 = 37 × (25 × 4) = 37 × 100 =3700

· 87 × 4 + 4 × 13 = (87 + 13) × 4 = 100 × 4 = 400

· 367 : 5 – 167 : 5 = ( 367 – 167) : 5 = 200 : 5 = 40

2. Приём округления.

· 399 + 473 = 400 +472 = 872

· 497 + 196 + 299 = 492 + 200 + 300 = 992

· 196 + 199 + 197 = 200 × 3 – 8 = 592

· 752 – 298 = 754 – 300 = 454

· 134 + 27 + 29 + 38 = 150 + 20 + 30 + 37 = 200 + 37 = 237

· 427 + 28 + 7 + 20 + 652 = 430 + 649 + 30 + 5 + 20 =

= 1079 + 1 + 54 = 1080 + 20 + 34 = 1134

· 198 × 3 = (200 – 2) × 3 = 600 – 6 = 594

· 35 × 18 = 35 × (20 – 2) = 700 – 70 = 630

3. Приём, основанный на зависимости результата от

изменения компонентов действий.

· 56 – 38 = 60 – 42 = 18

· 225 : 75 = (225 2) : (75 2) = 450 : 150 = 3

· 440 : 55 = 880 : 110 = 8

· 364 : 6 + 118 : 3 = 364 : 6 + 236 : 6 = (364 + 236) : 6 = 600 : 6 = 100

4. Приёмы последовательного умножения и деления.

· 75 × 8 = 75 × 2 × 2 × 2 = 150 × 2 × 2 = 300 × 2 = 600

· 35 × 18 = 35 × 2 × 9 = 70 × 9 = 630

· 23 × 55 = 23 × (5 × 11) = 115 × 11 = 1150 + 115 = 1 265

· 540 : 4 = (540 : 2) : 2 = 270 : 2 = 135

· 960 : 15 = (960 : 3) : 5 = 320 : 5 = 64

5. Приёмы умножения и деления на 5, 50, 500, 25, 250, 15, 125.

· 36 × 5 = (36 : 2) × 10 = 180

· 826 × 50 = (826 : 2) × 100 = 41 300

· 84 × 25 = (84 : 4) × 100 = 2 100

· 24 × 15 = 12 × 30 = 360

· 496 × 125 = (496 : 8) × 1000 = 62 000

· 4 340 : 5 = (4 340 : 10) × 2 = 868

· 4 000 : 125 = (4 000 × 8) : (125 × 8) = 32 000 : 1 000 = 32

6. Приёмы умножения на 9, 99, 11, 101. 1001.

· 26 × 9 = 25 × (10 – 1) = 250 – 25 = 225

· 35 × 99 = 3 500 – 35 = 3 465

· 37 × 11 = 37 × (10 + 1) = 370 + 37 = 407

· 73 × 101 = 7 300 + 73 = 7 373

· 735 × 1 001 = 735 000 + 735 = 735 735

Так, наблюдая и выявляя свойства чисел и действий над

ними, ученики накапливают сведения и используют их затем при

вычислениях. Овладение некоторыми приёмами рациональных

вычислений готовит детей к успешному изучению математики в

Источник

Действия с рациональными числами: правила, примеры, решения

Ниже рассмотрим правила основных математических действий над рациональными числами: сложение, вычитание, умножение и деление. Разберем теорию на практических примерах.

Действие сложения рациональных чисел

Рациональные числа содержат натуральные, тогда смысл действия сложения рациональных чисел сопоставим со смыслом сложения натуральных. Например, сумму рациональных чисел, записанную как 5 + 1 4 возможно описать следующим образом: к 5 целым предметам добавили четверть такого предмета, после чего полученное количество рассматривается совместно.

Сформулируем правила сложения рациональных чисел:

Сложение нуля с отличным от него рациональным числом

Прибавление нуля к любому числу дает то же число. Данное правило возможно записать в виде равенства: a + 0 = a (для любого рационального числа а). Используя переместительное свойство сложения, получим также верное равенство: 0 + a = a .

Пара простых примеров: сумма рационального числа 2 , 1 и числа 0 равно 2 , 1 и: 6 4 5 + 0 = 6 4 5 .

Сложение противоположных рациональных чисел

Сумма противоположных чисел равна нулю.

Данное правило можно записать в виде: a + ( — a ) = 0 (для любого рационального числа a ).

К примеру, числа 45 , 13 и — 45 , 13 являются противоположными, т.е. их сумма равно нулю: 45 , 13 + ( — 45 , 13 ) = 0 .

Сложение положительных рациональных чисел

В виде обыкновенной дроби возможно представить любое положительное рациональное число и использовать далее схему сложения обыкновенных дробей.

Необходимо произвести сложение рациональных чисел: 0 , 6 и 5 9 .

Решение

Выполним перевод десятичной дроби в обыкновенную и тогда: 0 , 6 + 5 9 = 6 10 + 5 9 .

Осуществим сложение дробей с разными знаменателями:

6 10 + 5 9 = 54 90 + 50 90 = 104 90 = 1 7 45

Ответ: 0 , 6 + 5 9 = 1 7 45 .

Рациональные числа, которые подвергают действию сложения, возможно записать в виде конечных десятичных дробей или в виде смешанных чисел и, таким образом, осуществить сложение десятичных дробей и смешанных чисел соответственно.

Сложение рациональных чисел с разными знаками

Для того, чтобы осуществить сложение рациональных чисел с разными знаками, необходимо из бОльшего модуля слагаемых вычесть меньший и перед полученным результатом поставить знак того числа, модуль которого больше.

Необходимо осуществить сложение рациональных чисел с разными знаками 8 , 2 и — 2 3 4 .

Решение

Согласно исходным данным, необходимо произвести сложение положительного числа с отрицательным. Придерживаясь вышеуказанного правила, определим модули заданных чисел: | 8 , 2 | = 8 , 2 и | — 2 3 4 | = 2 3 4 . Проведя сравнение модулей — рациональных чисел, получим: 8 , 2 > 2 3 4 и соответственно поймем, какое число из заданных станет уменьшаемым, а какое — вычитаемым. Произведем вычитание смешанных чисел, т.е.: 8 , 2 — 2 3 4 = 8 2 10 — 2 3 4 = 5 9 20 .

Полученному результату присваивается знак плюс, т.к. бОльшее из слагаемых по модулю – положительное число. Ответ: 8 , 2 + ( — 2 3 4 ) = 5 9 20 .

Сложение отрицательных рациональных чисел

Для того, чтобы произвести сложение отрицательных рациональных чисел, необходимо сложить модули заданных слагаемых, затем полученному результату присвоить знак минус.

Необходимо произвести сложение чисел: — 4 , 0203 и — 12 , 193 .

Решение

Модули заданных чисел соответственно равны: 4 , 0203 и 12 , 193 . Сложим их:

​​​​​​

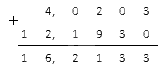
Полученному результату присваиваем знак минус: — 16 , 2133 .

Ответ: ( — 4 , 0203 ) + ( — 12 , 193 ) = — 16 , 2133 .

Действие вычитания рациональных чисел

Вычитание – действие, обратное сложению, в котором мы находим неизвестное слагаемое по сумме и известному слагаемому. Тогда из равенства c + b = a следует, что a — b = c и a — c = b . И наоборот: из равенств a — b = c и a — c = b следует, что c + b = a .

При вычитании из бОльшего положительного рационального числа мы либо производим вычитание обыкновенных дробей, либо, если это уместно, вычитание десятичных дробей или смешанных.

Необходимо вычислить разность рациональных чисел: 4 , ( 36 ) – 1 5 .

Решение

Сначала переведем периодическую десятичную дробь в обыкновенную: 4 , ( 36 ) = 4 + ( 0 , 36 + 0 , 0036 + … ) = 4 + 0 , 36 1 — 0 , 01 = 4 + 36 99 = 4 + 4 11 = 4 4 11

Далее переходим к действию вычитания обыкновенной дроби из смешанного числа: 4 , ( 36 ) — 1 5 = 4 4 11 — 1 5 = 4 + 4 11 — 1 5 = 4 + 20 55 — 11 55 = 4 + 9 55 = 4 9 55

Ответ: 4 , ( 36 ) — 1 5 = 4 9 55

В прочих случаях вычитание рациональных чисел необходимо заменить сложением: к уменьшаемому прибавить число, противоположное вычитаемому: a – b = a + ( — b ) .

Указанное равенство можно доказать, опираясь на свойства действий с рациональными числами. Они дают возможность записать цепочку равенств: ( a + ( — b ) ) + b = a + ( ( — b ) + b ) = a + 0 = a . Отсюда в силу смысла действия вычитания следует, что сумма a + ( — b ) есть разность чисел a и b .

Необходимо из рационального числа 2 7 вычесть рациональное число 5 3 7

Решение

Согласно последнему указанному правилу используем для дальнейших действий число, противоположное вычитаемому, т.е. — 5 3 7 . Тогда: 2 7 — 5 3 7 = 2 7 + — 5 3 7

Далее произведем сложение рациональных чисел с разными знаками: 2 7 + — 5 3 7 = — 5 3 7 — 2 7 = — 5 3 7 — 2 7 = — 5 1 7

Ответ: 2 7 + — 5 3 7 = — 5 1 7

Действие умножения рациональных чисел

Общее понятие числа расширяется от натуральных чисел к целым, так же как от целых к рациональным. Все действия с целыми числами имеют те же свойства, что и действия с натуральными. В таком случае, и действия с рациональными числами также должны характеризоваться всеми свойствами действий с целыми числами. Но для действия умножения рациональных чисел присуще дополнительное свойство: свойство умножения взаимообратных чисел. Вышесказанному соответствуют все правила умножения рациональных чисел. Укажем их.

Умножение на нуль

Произведение любого рационального числа a на нуль есть нуль.

Используя переместительное свойство умножения, получим: 0 · а = 0 .

К примеру, умножение рационального числа 7 13 на 0 даст 0 . Перемножив отрицательное рациональное число — 7 1 8 и нуль, также получим нуль. В частном случае, произведение нуля на нуль есть нуль: 0 · 0 = 0 .

Умножение на единицу

Умножение любого рационального числа a на 1 дает число a .

Т.е. a · 1 = a или 1 · a = a (для любого рационального a ). Единица здесь является нейтральным числом по умножению.

К примеру, умножение рационального числа 5 , 46 на 1 даст в итоге число 5 , 46 .

Умножение взаимообратных чисел

Если множители есть взаимообратные числа, то результатом их произведения будет единица. Т.е. : а · а — 1 = 1 .

К примеру, результатом произведения чисел 5 6 и 6 5 будет единица.

Умножение положительных рациональных чисел

В общих случаях умножение положительных рациональных чисел сводится к умножению обыкновенных дробей. Первым действием множители представляются в виде обыкновенных дробей, если заданные числа таковыми не являются.

Необходимо вычислить произведение положительных рациональных чисел 0 , 5 и 6 25 .

Решение

Представим заданную десятичную дробь в виде обыкновенной 0 , 5 = 5 10 = 1 2 .

Далее произведем умножение обыкновенных дробей: 1 2 · 6 25 = 6 50 = 3 25 .

Ответ: 0 , 5 · 6 25 = 3 25

Можно также работать и с конечными десятичными дробями. Удобнее будет в данном случае не переходить к действиям над обыкновенными дробями.

Необходимо вычислить произведение рациональных чисел 2 , 121 и 3 , 4 .

Решение

Перемножим десятичные дроби столбиком:

Ответ: 2 , 121 · 3 , 4 = 7 , 2114

В частных случаях нахождение произведения рациональных чисел представляет собой умножение натуральных чисел, умножение натурального числа на обыкновенную или десятичную дробь.

Умножение рациональных чисел с разными знаками

Чтобы найти произведение рациональных чисел с разными знаками, необходимо перемножить модули множителей и полученному результату присвоить знак минус.

Необходимо найти произведение чисел: — 3 3 8 и 2 1 2

Решение

Согласно вышеуказанному правилу получим: — 3 3 8 · 2 1 2 = — 3 3 8 · 2 1 2 = — 3 3 8 · 2 1 2

Заменим смешанные дроби неправильными и найдем искомое произведение: — 3 3 8 · 2 1 2 = — 27 8 · 5 2 = — 135 16 = — 8 7 16

Ответ: — 3 3 8 · 2 1 2 = — 8 7 16

Умножение отрицательных рациональных чисел

Для того, чтобы найти произведение отрицательных рациональных чисел, необходимо перемножить модули множителей.

Необходимо найти произведение отрицательных рациональных чисел — 3 , 146 и — 56 .

Решение: модули заданных чисел соответственно равны 3 , 146 и 56 .

Перемножим их столбиком:

Полученный результат и будет являться искомым произведением.

Ответ: ( — 3 , 146 ) · ( — 56 ) = 176 , 176

Деление рациональных чисел

Деление – действие, обратно умножению, в ходе которого мы находим неизвестный множитель по заданному произведению и известному множителю. Смысл действия деления можно записать так: из равенства b · c = a следует, что a : b = c и a : c = b . И наоборот: из равенств a : b = c и a : c = b следует, что b · c = a .

На множестве рациональных чисел деление не считается самостоятельным действием, поскольку оно производится через действие умножения. Собственно, этот смысл заложен в правило деления рациональных чисел.

Разделить число а на число b , отличное от нуля – то же самое, что умножить число a на число, обратное делителю. Т.е., на множестве рациональных чисел верно равенство: a : b = a · b — 1 .

Указанное равенство доказывается просто: на основе свойств действий с рациональными числами справедливой будет цепочка равенств ( a · b — 1 ) · b = a · ( b — 1 · b ) = a · 1 = a , которая и доказывает равенство a : b = a · b — 1 .

Таким образом, деление рационального числа на другое рациональное число, отличное от нуля, сводится к действию умножения рациональных чисел.

Необходимо выполнить действие деления 3 1 3 : — 1 1 6

Решение

Определим число, обратное заданному делителю. Запишем заданный делитель в виде неправильной дроби: — 1 1 6 = — 7 6 .

Число, обратное этой дроби, будет: — 6 7 . Теперь, согласно вышеуказанному правилу, произведем действие умножения рациональных чисел: 3 1 3 — 1 1 6 = 3 1 3 · — 6 7 = 10 3 · ( — 6 7 ) = — ( 10 3 · 6 7 ) = — 20 7 = — 2 6 7

Ответ: 3 1 3 : — 1 1 6 = — 2 6 7

Источник