Как добраться существует только два способа

Вам нужно подняться по лестнице. За один раз можно подняться на одну или две ступеньки. Сколько существует способов добраться до N-й ступеньки?

Авторизуйтесь

Вам нужно подняться по лестнице. За один раз можно подняться на одну или две ступеньки. Сколько существует способов добраться до N-й ступеньки?

Начало здесь простое. Вы стоите на лестничном марше и хотите подняться на первую ступеньку — № 1. Для этого надо сделать всего одно действие — подняться на одну ступеньку вверх. Теперь давайте рассмотрим вторую ступеньку, то есть N = 2. Чтобы подняться на неё, имеются два варианта. Вы можете сделать два шага — по одной ступеньке за раз или сразу подняться на вторую ступеньку.

Это практически вся информация, которая нужна вам для решения этой задачи. Чтобы понять, почему, представьте, что вашей целью является ступенька № 3. Впервые в этой ситуации вы не можете попасть на неё одним движением. здесь потребуется комбинация шагов. Существует только два способа попадания на ступеньку № 3: либо в виде короткого одиночного шага (со ступеньки № 2), либо двойного шага (со ступеньки № 1). Мы уже знаем, что для подъема на ступеньку № 1 имеется лишь один вариант. Мы также знаем, что есть всего два способа подняться на ступеньку № 2. Сложите эти варианты (1 + 2 = 3), и вы получите число способов, позволяющих подняться на ступеньку № 3.

Та же самая логика применяется для подъема на каждую следующую ступеньку. Существует два способа, чтобы подняться на ступеньку № 4 — со ступеньки № 2 или со ступеньки № 3. Добавьте число способов подъема на ступеньку № 2 (2) к числу способов, позволяющих оказаться на ступеньке № 3 (3). Это даёт 5 вариантов — число способов, позволяющих оказаться на ступеньке № 4.

Легко продолжить эту серию и дальше. С увеличением числа ступенек число способов подниматься по ним нарастает, как снежный ком, что можно представить в следующем виде:

Любому человеку с математической подготовкой нижняя серия покажется до боли знакомой. Так оно и есть. Это последовательность Фибоначчи. (Чуть подробнее о ней ниже.) Интервьюер хочет получить ответ для общего случая из N ступенек.

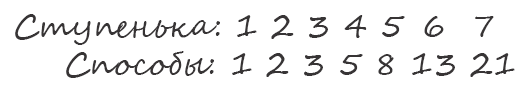
Это просто число Фибоначчи под номером N. Леонардо Фибоначчи, также известный как Леонардо Пизанский, был самым влиятельным итальянским математиком в Средние века. Именно Фибоначчи понял невероятное превосходство арабскo-индийской позиционной системы исчисления по сравнению с римским обозначением цифр, которое все ещё использовалось в средневековой Европе. При помощи арабско-индийской системы умножение и деление можно было свести к алгоритму (еще одно арабское слово). При применении римских чисел эти операции на практике выполнять было сложно. Торговцам приходилось приглашать экспертов и дорого им платить за вычисления, которые те осуществляли при помощи абаков. В 1202 году Фибоначчи написал Liber abaci — руководство по использованию абака, в котором он расхваливал арабские числа своим читателям, которые были, скорее всего, настроены к ним скептически. В этой книге также описывается и та серия чисел, которую мы теперь называем по его фамилии. Однако её изобрел не Фибоначчи. Эта последовательность была известна еще индийским ученым, жившим в VI веке.

Напишите 1, а затем добавьте еще 1 рядом. Сложите их и получите сумму (2), которая затем добавляется к формируемой последовательности:

Для получения каждого нового члена лишь складывайте последние два числа в ряду/ Серия примет следующий вид.

1 1 2 3 5 8 13 21 34 55 89 144…

Поклонники теории заговоров отыскивают серии Фибоначчи в самых неожиданных местах. Хотите перевести расстояние из миль в километры? Воспользуйтесь соседними числами Фибоначчи (55 миль в час = 89 километров в час). В следующий раз, когда у вас окажется свободное время, посчитайте небольшие дольки, из которых состоит кожура ананаса, и вы обнаружите, что они образуют два накладывающихся друг на друга набора спиралей, идущих в противоположных направлениях. В одной из них восемь долей, в другой тринадцать. Оба этих числа относятся к серии Фибоначчи. Аналогичные закономерности можно увидеть в сосновых шишках, подсолнухах и артишоках. Случайность? Вряд ли, если учесть тот факт, что последовательность Фибoначчи проявила себя и в Коде Да Винчи (в виде комбинации для вскрытия сейфа), и в этом вопросе на собеседовании, который задают в компании, стремящейся к информационному доминированию во всем мире (Google, если вы не поняли).

Источник

Как добраться до Мёртвого моря

Мёртвое море – просто удивительное место, побывать в котором мечтает каждый человек. Здесь можно зарядиться здоровьем и энергией, избавиться от различных заболеваний, отдохнуть от суеты и понежиться в теплой соленой воде с уникальным целебным составом.

Огромное количество минералов, содержащихся в этой воде, способно избавить от ревматизма и других заболеваний суставов, снизить лишний вес, вылечить депрессию и нервные заболевания – не существует ни одной болезни, которая не прошла бы в этом потрясающем море. Разве может быть что-то лучше, чем лежать на спине, любоваться лазуревым небом с белоснежными облаками, покачиваясь на ласковых волнах Мертвого моря? Вы почувствуете, как все заботы и тревоги уходят в сторону, уступая место безграничному счастью и полному расслаблению.

Утонуть здесь просто невозможно – вода держит вас на поверхности так нежно, словно вы катаетесь на облачке. Здесь не обязательно уметь плавать – достаточно просто лечь на поверхность воды, и наслаждаться безмятежным отдыхом, ощущая, как с каждой минутой вам становится все лучше и лучше, появляются силы и энергия, а усталость и тревоги отступают в сторону. В этом месте абсолютно не важен ваш социальный статус и финансовое положение – Мертвое море принимает всех.

Ежедневно на побережье Мертвого моря съезжаются тысячи туристов со всего мира – это место и в самом деле стоит того, чтобы посетить его хотя бы раз в жизни.

Как добраться до Мертвого моря

Многие туристы, только приземлившись в Бен-Гурион, мечтают сразу же отправиться на Мертвое море. Аэропорт – просто идеальная отправная точка, ведь существует множество способов добраться отсюда до выбранного курорта.
Добраться до этого чуда света можно из любого уголка страны – оно находится в самом центре страны. Из большинства городов Израиля до побережья ходит различный транспорт, а среднее время поездки займет около двух часов неспешной езды. Добраться можно множеством способов: такси, автобусы, личные автомобили.

К примеру, экскурсионные туры предлагает множество компаний – достаточно открыть сайты турагентств, и вы увидите сотни предложений. К минусам такой поездки можно отнести необходимость провести время проездки в душном автобусе вместе с десятками других туристов – согласитесь, не очень заманчивая перспектива?

Гораздо проще добраться до Мёртвого моря самостоятельно – вы можете построить свой личный маршрут, познакомиться с достопримечательностями и окрестностями израильских городов, избавитесь от необходимости общаться с другими туристами. Сделать это невероятно просто — в этой статье мы расскажем о том, как добраться до Мертвого моря из любого города Израиля и примерные цены, в которые выльется такая поездка. Стоит учитывать, что цена зависит от сезона, поэтому мы указали только примерную стоимость поездки. Итак, поехали – лучшие лайфхаки на тему того, как поскорее добраться до Мертвого моря и при этом сэкономить свои деньги и время.

Как добраться из Иерусалима до Мертвого моря

Расстояние между Иерусалимом и Мертвым морем небольшое – всего 116 километров, которые легко преодолеть примерно за час поездки на любом виде транспорта. Проще всего добраться на трех автобусах.

Автобус № 444 идет до Эйлата, и доберетесь вы на нем только до региона Тамар. Оттуда вам придется добираться до нужной вам точки Мертвого моря на других автобусах или поездах. Этот автобус ежедневно отправляется с Центрального автовокзала в 7.00, в 10.00, в 14.00, и в 17.00. Поездка стоит 42 шекеля (12 долларов — это около 900 рублей). Суббота и воскресенье выходные. Выбирая этот рейс, стоит позаботиться о бронировании билетов заранее – поскольку это прямой рейс до Эйлата, то пассажиров очень много.

Автобус № 486 довезет вас прямиком в Эйн Бокек — Неве Зоар. Это так называемый район самых лучших гостиниц на побережье. Этот рейс очень нравится туристам, ведь маршрут проложен через самые популярные пляжи Мертвого моря – Калию и Минерал, Эйн-Геди и Хамей – Зоар. Он совершает 8 рейсов в сутки — в 8.00, в 8.50, в 9.30, в 10.30, в 11.30, в 12.30, в 13.30, в 16.15. Стоимость поездки до конечной остановки составляет 42 шекеля (около 12 долларов), но цена зависит от того, на какой именно пляж вы хотите попасть. Если вы берете билеты в обе стороны («туда — обратно»), водитель сделает скидку в 15%. Среднее время в пути – 2 часа.

На автобусе № 487 «Иерусалим – Калия» вы с ветерком доберетесь до северных пляжей и кибуца Калия (небольшая, но очень красивая деревушка). С воскресенья по четверг автобус отправляется в 15:15 и 20:40, в пятницу автобус отправляется к Мертвому морю в 16:15. Вернуться в Иерусалим можно с утренним рейсом в 6:59.

Все автобусы отправляются с Центрального автовокзала ежедневно. Рейсы постоянные – в среднем, с понедельника по четверг каждый из автобусов совершает около 7 поездок в день.

Трансфер из Тель-Авива на Мертвое море

Добраться отсюда до Мертвого моря не очень просто – существует только два способа это сделать. Первый – это такси в Израиле, которое довезет вас в любую точку страны максимально быстро и комфортно. Второй – автобус № 421 « Тель – Авив – Спа Эйн- Геди». Маршрут построен очень удачно – вы сможете добраться до большинства популярных израильских пляжей, кроме кибуца Калия. С воскресенья по четверг атвобус отправляется из Терминала Арлозоров в 9:00 и 12:00, в пятницу в 9:00. По субботам рейсов нет – обязательно учитывайте этот момент.

Стоимость поездки около 43 шекелей (12,5 долларов). Среднее время поездки составляет около 2,5 часов – за это время вы успеете полюбоваться местными достопримечательностями и потрясающими видами природы.
Кроме того, добраться до Мертвого моря можно с пересадками – вначале добраться до Иерусалима, и уже оттуда уехать с одним из регулярных рейсов. Сделать это можно как с Новой центральной станции, так и из терминала Арлозоров. В среднем, автобусы ходят каждый 10-20 минут, а стоимость поездки составит около 5 шекелей (4 доллара).

Как добраться из Нетании до Мертвого моря

Если вы решили отправиться на курорты Мертвого моря из этого удивительного городка, то вам придется потратить немного своего времени – отсюда нет ни одного прямого рейса до побережья. Безусловно, всегда есть экскурсионные автобусы – как правило, они стоят возле любого отеля и совершают регулярные (даже в выходные дни) рейсы. Такие экскурсии в Израиле очень популярны – это еще один минус данного способа передвижения, ведь в автобусе будет просто огромное количество пассажиров. Опытный экскурсовод расскажет вам про все достопримечательности, встречающиеся по пути, но стоимость поездки обойдется вам в 50-60 долларов. Гораздо проще добраться с пересадками: вначале доехать до Иерусалима или Тель – Авива, и уже оттуда сесть на один из регулярных рейсов до нужного вам пляжа.

Примерный маршрут может быть таким: на центральном автовокзале Нетании садитесь на автобус № 947, следующий до Иерусалима. Время поездки около 2 часов, а стоимость составит примерно 30 шекелей (8 долларов). Затем, никуда не выходя из здания, пересаживаетесь на автобус № 486 – еще два часа, и вы на Мертвом море.

Как добраться из Хайфы до Мертвого моря

Это очень красивый город, в котором непременно найдется, на что посмотреть. Единственным его недостатком можно считать невозможность добраться напрямую до побережья Мертвого моря – придется вновь строить маршрут с пересадками. Проще всего добраться до Иерусалима – отсюда следует больше всего рейсов до Мертвого моря. Вы можете выбрать один из трех автобусов, которые ежедневно совершают поездки в нужное вам место – вы сможете посетить любой выбранный вами пляж.

Если вы привыкли к комфорту и не хотите трястись в переполненном автобусе вместе с другими пассажирами, вам стоит заранее позаботиться о бронировании такси. Этот способ передвижения придется по вкусу даже самым требовательным пассажирам: опытный водитель, который расскажет про все достопримечательности и покажет самые красивые места Израиля, прохладный воздух в салоне автомобиля, возможность заехать на любой пляж и полюбоваться местными видами природы. Стоит прокат автомобиля недорого – все зависит от дальности поездки.

Наша компания предлагает трансфер в аэропорт и из него – мы довезем вас до самых лучших курортов Мертвого моря или до гостиницы, где вы сможете переодеться перед тем, как отправиться в это удивительное место, попасть в которое мечтает каждый.

Источник

Как добраться существует только два способа

На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт К, не проходящих через пункт В?

Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х.

При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.

С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:

Е = Д = 1 (В не учитываем, поскольку путь не должен проходить через город В).

К = Ж + Е + И + Д = 5.

Примечание. Необходимо найти количество различных путей из города А в город К, не проходящих через город В.

На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт К, не проходящих через пункт Е?

Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х.

При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.

С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:

И = В + Г = 5 (Е не учитываем, поскольку путь не должен проходить через город Е).

Примечание. Необходимо найти количество различных путей из города А в город К, не проходящих через город Е.

На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт Л, проходящих через пункт И?

Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х.

При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.

С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:

Г = А + Б + В + Ж = 4

К = И = 10. (Е не учитываем, поскольку путь должен проходить через И)

Примечание. Необходимо найти количество различных путей из города А в город Л, проходящих через город И.

Приведем другое решение.

Количество путей из пункта А в пункт Л, проходящих через пункт И, равно произведению количества путей из пункта А в пункт И В и количества путей из пункта И в пункт Л.

Найдем количество путей из пункта А в пункт И:

Г = А + Б + В + Ж = 4

Из пункта И в пункт Л есть только один путь И — К — Л.

Тогда количество путей из пункта А в пункт Л, проходящих через пункт И, равно 10 · 1 = 10.

На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт Л, проходящих через пункт Е?

Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х.

При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.

С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:

Г = А + Б + В + Ж = 4

К = Е = 10. (И и В не учитываем, поскольку путь должен проходить через город Е).

Л = К + Е = 20. (Д и Ж не учитываем, поскольку путь должен проходить через город Е).

Примечание. Необходимо найти количество различных путей из города А в город Л, проходящих через город Е.

Приведем другое решение.

Количество путей из пункта А в пункт Л, проходящих через пункт Е, равно произведению количества путей из пункта А в пункт Е и количества путей из пункта Е в пункт Л.

Найдем количество путей из пункта А в пункт Е:

Г = А + Б + В + Ж = 4

Найдем количество путей из пункта Е в пункт Л (при этом Е — исходный пункт):

Тогда количество путей из пункта А в пункт Л, проходящих через пункт Е, равно 10 · 2 = 20.

На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт Л, не проходящих через пункт Е?

Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х.

При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.

С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:

И = Г = 3 (Е не учитываем, поскольку путь не должен проходить через город Е).

К = И = 3 (Е не учитываем, поскольку путь не должен проходить через город Е).

Л = Д + Ж + К = 3 + 3 + 3 = 9 (Е не учитываем, поскольку путь не должен проходить через город Е).

На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К, проходящих через город Д?

Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х.

При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.

С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:

Е = Д = 3 (В и Г не учитываем, поскольку путь должен проходить через город Д).

Примечание. Необходимо найти количество различных путей из города А в город К, проходящих через город Д.

Приведем другое решение.

Количество путей из города А в город К, проходящих через город Д, равно произведению количества путей из города А в город Д и количества путей из города Д в город К.

Найдем количество путей из города А в город Д:

Найдем количество путей из города Д в город К (при этом Д — исходный пункт):

Тогда количество путей из города А в город К, проходящих через город Д, равно 3 · 3 = 9.

На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К, проходящих через город Г?

Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х.

При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.

С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:

Е = Г = 3 (В и Д не учитываем, поскольку путь должен проходить через город Г).

Примечание. Необходимо найти количество различных путей из города А в город К, проходящих через город Г.

Приведем другое решение.

Количество путей из города А в город К, проходящих через город Г, равно произведению количества путей из города А в город Г и количества путей из города Г в город К.

Найдем количество путей из города А в город Г:

Найдем количество путей из города Г в город К (при этом Г — исходный пункт):

Тогда количество путей из города А в город К, проходящих через город Г, равно 3 · 3 = 9.

На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, К, Л, М, Н, П. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.

Сколько существует различных путей из города А в город П, проходящих через город Е?

Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х. При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.

С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:

Ж = Е = 3. (В и Г не учитываем, поскольку в этих вершинах не проходим через Е).

Примечание. Необходимо найти количество различных путей из города А в город П, проходящих через город Е.

Приведем другое решение.

Заметим, что путь из города А в город П обязательно должен проходить через город Ж. По условию задачи путь должен также проходить через город Е. Тогда количество путей из города А в город П, проходящих через город Е, равно произведению количества путей из города А в город Е, количества путей из города Е в город Ж и количества путей из города Ж в город П.

Найдем количество путей из города А в город Е:

Из города Е в город Ж есть только один путь.

Найдем количество путей из города Ж в город П (при этом Ж — исходный пункт):

Тогда количество путей из города А в город П, проходящих через город Е, равно 3 · 1 · 7 = 21.

На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, К, Л, М, Н, П. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.

Сколько существует различных путей из города А в город П, проходящих через город В?

Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х. При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.

С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:

Ж = В = 3. (Е и Г не учитываем, поскольку в этих вершинах не проходим через В).

Примечание. Необходимо найти количество различных путей из города А в город П, проходящих через город В.

Приведем другое решение.

Заметим, что путь из города А в город П обязательно должен проходить через город Ж. По условию задачи путь должен также проходить через город В. Тогда количество путей из города А в город П, проходящих через город В, равно произведению количества путей из города А в город В, количества путей из города В в город Ж и количества путей из города Ж в город П.

Найдем количество путей из города А в город В:

Из города В в город Ж есть только один путь.

Найдем количество путей из города Ж в город П (при этом Ж — исходный пункт):

Тогда количество путей из города А в город П, проходящих через город В, равно 3 · 1 · 7 = 21.

На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, К, Л, М, Н, П. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.

Сколько существует различных путей из города А в город П, проходящих через город М?

Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х. При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.

С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:

Л = М = 17 (Ж и К не учитываем, поскольку путь должен проходить через М).

П = Л + М = 34 (К не учитываем, поскольку путь должен проходить через М).

Примечание. Необходимо найти количество различных путей из города А в город П, проходящих через город М.

Приведем другое решение.

Количество путей из города А в город П, проходящих через город М, равно произведению количества путей из города А в город М и количества путей из города М в город П.

Найдем количество путей из города А в город М:

Найдем количество путей из города М в город П (при этом М — исходный пункт):

Тогда количество путей из города А в город П, проходящих через город М, равно 17 · 2 = 34.

На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.

Сколько существует различных путей из города А в город К, не проходящих через пункт В?

Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х. При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.

С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:

Г = А = 1 (В не учитываем, поскольку путь не должен проходить через город В).

Д = Б = 1 (В не учитываем, поскольку путь не должен проходить через город В).

Е = Г + Д = 2 (В не учитываем, поскольку путь не должен проходить через город В).

К = Д + Ж + И + Е = 5.

Примечание. Необходимо найти количество различных путей из города А в город К, не проходящих через город В.

На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.

Сколько существует различных путей из города А в город К, не проходящих через пункт В?

Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х. При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.

С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:

Г = А = 1 (В не учитываем, поскольку путь не должен проходить через город В).

Д = Б = 1 (В не учитываем, поскольку путь не должен проходить через город В).

Е = Г + Д = 2 (В не учитываем, поскольку путь не должен проходить через город В).

Примечание. Необходимо найти количество различных путей из города А в город К, не проходящих через город В.

Источник