Измерение ускорения свободного падения различными способами

Измерение ускорения свободного падения разными методами
опыты и эксперименты по физике (9 класс) на тему

Экспериментально измерить ускорения свободного падения разными методами и выяснить, какой из них более всего приближен к табличному значению.

Скачать:

Вложение	Размер
issledovatelskaya_rabota.docx	297.81 КБ

Предварительный просмотр:

Муниципальное общеобразовательное учреждение

« Лицей №11 Ворошиловского района Волгограда»

Открытый городской конкурс

Старшеклассников в рамках

Городского научного общества

Учащихся “Я и Земля”

Измерение ускорения свободного падения разными методами

Ученики 9 класса «А» МОУ Лицей №11

Лачугина Вера Алексеевна,

Меренкова Ксения Петровна.
Руководитель:
Маканова Людмила Генриховна.

г. Волгоград
2017 г

Содержание:

История открытия ускорения свободного падени…………………………..4

Методы измерения ускорения свободного падения. 6

Практическая часть. 7

Цель работы:

Экспериментально измерить ускорения свободного падения разными методами и выяснить, какой из них более всего приближен к табличному значению.

• Провести измерения различных физических величин для определения ускорения свободного падения (самостоятельно).
• Выяснить, какой из методов даст более точный результат ,согласно табличным данным
• Приобрести навык работы с физическими приборами
• Научиться оценивать погрешность измерения.

Обоснование выбора темы:

Ускорение свободного падения на Земле на высотах не превышающих 100 метров можно считать постоянным и равным 9,8 м/с 2 . У поверхности Земли ускорение свободного падения одинаково не везде, причина в том, что : 1)экваториальный радиус Земли больше полярного

2) сплюснутость у полюсов;

3) вращение Земли.

Точное значение ускорения свободного падения находит применение в практической деятельности людей.

• при траекторных расчетах искусственных спутников Земли.
• в геофизике: распределении масс внутри и вне Земли;
• в геологии — при поиске полезных ископаемых;

Из школьного курса физики мы знаем, что на все тела действует сила тяжести, F т = mg. Эта сила влияет на движение тел. При решении задач необходимо учитывать эту силу.

При выполнении экспериментальных работ значение ускорения свободного падения, не всегда точно совпадает с тем, которое взято из справочного материала и применяется при решении задач. Из дополнительной литературы мы выяснили , что существует много способов измерения ускорения свободного падения, захотелось самостоятельно опробировать некоторые из них .а может быть изобрести и свой метод. Поэтому мы считаем, что тема актуальна.

Ускорение свободного падения.

В Древней Греции механические движения делились на естественные и неестественные.

Ученый древней Греции Аристотель утверждал, что тело падает на Землю быстрее, если его масса больше. Впервые поспорил с Аристотелем, итальянский ученый физик Галилео Галилей . Он отказался от древнегреческого деления механических движений, и впервые стал использовать физические понятия равномерного и равноускоренного движений. Исследовал механическое движение измеряя расстояния и временя движения.

Особое внимание Галилей уделял исследованию свободного падения тел. Хорошо известны его эксперименты с использованием наклонной башни в городе Пизе. Галилей одновременно ронял с башни полуфунтовый шар и стофунтовую бомбу .И шар . и бомба достигали поверхности Земли почти одновременно: бомба опередила шар всего на несколько дюймов. Галилео еще в то время объяснил это наличием сопротивления воздуха. Такое объяснение являлось гениальным .В своих работах он опроверг еще одно заблуждение, считалось, что если на тело не действует сила , то движение должно прекратиться. Галилей впервые открывает закон инерции. Он писал, что если на тело действует сила, то результат ее действия не зависит покоится ли тело или движется. При свободном падении на тело постоянно действует сила притяжения, по закону инерции действие сохраняется. Это утверждение принято основой законов свободного падения.

Галилей определил ускорение свободного падения с большой погрешностью. Им было измерено, что если шар падает с высоты 50 м в течение 4 с., то нельзя точно определить g, так как в то время когда жил Галилей не было точного прибора для измерения времени .Средства измерения времени: песочные, водяные часы или изобретенные им часы с маятником не давали большой точности отсчета времени (по сравнению с электронными часами существующие в наше время ) В 1660 г ускорение свободного падения было точно определено Христианом Гюйгенсом .

Чтобы достигнуть большей точности измерений, Галилей предложил уменьшить скорость падения тел. Так стали использовать наклонную плоскость для опытов..

Желоб проделали в доске и поставили наклонно. По нему катился латунный шар. Но как более точно измерить время движения ? Галилей на дне большого сосуда с водой проделал отверстие, через которое вытекала тонкая струя. Она направлялась в маленький сосуд, который предварительно взвешивался. Промежуток времени измерялся по приращению веса сосуда! Пуская шар с половины, четверти и т. д. длины наклонной плоскости, Галилей установил, что пройденные шаром пути относились как квадраты времени движения.

S 1 :S 2 :S 3 = t 1 2 :t 2 2 :t 3 2

Создание воздушных насосов, позволило произвести эксперименты со свободным падением тел в вакууме. И. Ньютон выкачал воздух из длинной стеклянной трубки и бросил сверху одновременно птичье перо и золотую монету. Эти тела сильно различающиеся по своей плотности падали с одинаковой скоростью. Этот опыт доказал предположения Галилея. Опыты, Галилея привели к простому правилу. Это правило в случае свободного падения тел в воздухе выполняется с ограниченной точностью. Поэтому верить в него, как в идеальный случай нельзя. Для полного изучения свободного падения тел необходимо знать, какие при падении происходят изменения физических величин: температуры, давления, и др., то есть исследовать все стороны этого явления. Эти исследования были бы очень сложными, заметить их взаимосвязь было бы трудно, поэтому часто в физике приходится довольствоваться лишь тем, что правило представляет собой некое упрощение единого закона.

. Галилей не только проверил опытом и отстаивал свое правило, но и установил вид движения тела, падающего по вертикали: “. естественное движение падающего тела непрерывно ускоряется”.

Методы измерения ускорения свободного падения.

Существует много способов определения ускорения свободного падения, мы проделали всего четыре:

• Определение ускорения свободного падения с помощью математического маятника. (Опыт № 1)
• Определение ускорения свободного падения с помощью двойного математического маятника. (Опыт №2)
• Определение ускорения свободного падения традиционным способом (как делал Галилей). (Опыт № 3)
• Определение ускорения свободного падения с помощью прибора для изучения движения тел.(Опыт №4)

Некоторые из этих опытов не требуют специального оборудования, достаточно знать формулу, где h высота падения тела, t время за которое тело достигло земли.

Например : Определение ускорения свободного падения традиционным способом (как делал Галилей).

Практическая часть:

Опыт №1.

Тема : Определение ускорения свободного падения с помощью математического маятника.

Оборудование : часы с секундной стрелкой, измерительная лента с погрешностью л=0,5 см, шарик с отверстием, нить, штатив с муфтой и кольцом.

1. Установили штатив, у его верхнего конца укрепили при помощи муфты кольцо и подвесили к нему шарик на нити. Шарик должен висеть на расстоянии 2-5 см от пола.
2. Измерили лентой длину маятника.
3. Отклонили маятник от его положения равновесия на 5-8 см и отпустили его.
4. Измерили время 40 полных колебаний.
5. Повторили опыт еще 2 раза.
6. Вычислили среднее значение времени колебаний.
7. Вычислили среднее значение периода колебаний.
8. Результаты измерений занесли в таблицу.

Источник

Различные способы определения ускорения свободного падения Выполнила: ученица 10 «А» класса МКОУ СОШ 2 Нотова Анастасия Руководитель: Гребенщикова Татьяна. — презентация

Презентация была опубликована 8 лет назад пользователемЕлизавета Пантюхина

Похожие презентации

Презентация 10 класса по предмету «Физика и Астрономия» на тему: «Различные способы определения ускорения свободного падения Выполнила: ученица 10 «А» класса МКОУ СОШ 2 Нотова Анастасия Руководитель: Гребенщикова Татьяна.». Скачать бесплатно и без регистрации. — Транскрипт:

1 Различные способы определения ускорения свободного падения Выполнила: ученица 10 «А» класса МКОУ СОШ 2 Нотова Анастасия Руководитель: Гребенщикова Татьяна Сергеевна учитель физики высшей категории

2 Если все свободно падающие тела движутся одинаково, то это движение само по себе заслуживает детального исследования. Эрик Роджерс, «Физика для любознательных».

3 Цель работы: Определение ускорения свободного падения различными способами.

4 Задачи: Изучить литературу по данной теме. Ознакомиться с историей открытия свободного падения. Рассмотреть способы определения ускорения свободного падения. Провести самостоятельные измерения ускорения свободного падения разными способами. Определить наиболее точные способы определения ускорения свободного падения.

5 Свободное падение Свободное падение равноускоренное движение, под действием силы тяжести. Свободное падение представляет собой частный случай равномерно ускоренного движения без начальной скорости.

6 В конце XVI века знаменитый итальянский ученый Г. Галилей опытным путем с доступной для того времени точностью установил, что в отсутствие сопротивления воздуха все тела падают на Землю равноускоренно, и что в данной точке Земли ускорение всех тел при падении одно и то же. До этого в течение почти двух тысяч лет, начиная с Аристотеля, в науке было принято считать, что тяжелые тела падают на Землю быстрее легких.

7 Ускорение свободно падающего тела Экспериментально установлено, что ускорение свободного падения не зависит от массы падающего тела, но зависит от географической широты местности и высоты подъёма над земной поверхностью.

8 Зависимость ускорения свободного падения от радиуса Земли и высоты тела над Землёй непосредственно вытекает из формулы всемирного тяготения. Независимость этого ускорения от массы падающего тела следует из второго закона Ньютона и закона всемирного тяготения.

9 Реальное ускорение свободного падения на поверхности Земли может быть вычислено по эмпирической формуле: g= 9, [1+0, sin 2 (φ) – 0, sin 2 (2φ) ] – 3,086 · ·h, где φ широта рассматриваемого места, h высота над уровнем моря.

10 Значение гравитационного ускорения на поверхности планеты можно приблизительно подсчитать, представив планету точечной массой M, и вычислив гравитационное ускорение на расстоянии её радиуса R: где G гравитационная постоянная (6,6742*10-11 м 3 с- 2 кг- 1 ).

11 Отличия обусловлены: центростремительным ускорением в системе отсчёта, связанной с вращающейся Землёй; неточностью формулы из-за того, что масса планеты распределена по объёму, который, кроме того, имеет не шарообразную форму; неоднородностью Земли, что используется для поиска полезных ископаемых по гравитационным аномалиям.

12 Измерение ускорения свободного падения с помощью вращающегося диска 1) h 1 = 10 см. = 0,1 м., h 2 = 20 см. = 0,2 м., t = φ/ 468° = 40°/468° = 0,09 с. g = 2*(h 1 — h 2 ) 2 / t 2 = 2*(0,1 — 0,25) 2 / 0,092 = 9,9 м/с 2. 2) h 1 = 20 см. = 0,2 м., h 2 = 50 cм. = 0,5 м., t = φ/ 468° = 360° / 468° = 0,13 с. g = 2*(h 1 — h 2 ) 2 / t 2 = 2*(0,2 — 0,5) 2 / 0,132 = 9,9 м/с 2. опыта Высота падения первого шара, h 1, м. Высота падения второго шара, h 2, м. Интервал времени между падением шаров, t, с. Ускорение свободного падения, g, м/с ,1 м.0,25 м.0,09 с.9,9 м/с 2 2.0,2 м.0,5 м.0,13 с.9,9 м/с 2

13 Измерение ускорения свободного падения методом капельницы g= 2h/t 2 = 0.6/ = 8,9 м/с 2 Вывод: Ускорение свободного падения с помощью капельницы определяется с погрешностью. h, м.t, c.g, м/с 2 0,3 м0,26 с8,9 м/с 2

14 Измерение ускорения свободного падения с помощью наклонной плоскости (опыт с шариком) g ср = 2*h/t ср 2 g ср = 2*0.44/ = м/с 2. опыта t, c.t ср, c.t, c.t cр, c.h, м.g ср, м/с с с с с.0.44 с.9,804 м/с с с с с с с с с.

15 Измерение ускорения свободного падения с помощью наклонной плоскости (опыт с монеткой) t=(t 1 +t 2 +t 3 )/3= ( )/3=0.54 c. a= 2s/t 2 =2*0.2/ = 1.4 м/с 2. Sin α= h/s=0.08/0.2=0.4 Cos α=1- sin 2 α=0.9 Вычислим ускорение свободного падения без учета трения. g= a/( sin α — cos α)= 2.8 м/с 2. Вычислим ускорение свободного падения с учетом трения. g= a/( sin α — μ cos α)= 9,46 м/с 2. опыта S, м.h, м.t, с. a, м/с 2. SinαCos αg,м/с 2.(бе з учета трения) g,м/с 2.(с учетом трения, μ= 0,28 ) 10.2 м.0.08 м.0.58 с.0.54 с.1.4 м/с м/с 2 9,46 м/с м.0.67 с м.0.36 с.

16 Анализ полученных результатов Методыg, м/с 2 С помощью вращающегося диска9.9 м/с 2 Методом капельницы8,9 м/с 2 С помощью наклонной плоскости (опыт с шариком) 9,804 м/с 2 С помощью наклонной плоскости (опыт с монеткой без учета трения) 2.8 м/с 2 С помощью наклонной плоскости (опыт с монеткой с учетом трения) 9,46 м/с 2

17 заключение В ходе исследования мной были рассмотрены несколько способов измерения ускорения свободного падения. Проанализировав полученные результаты, я пришла к выводу о том, что самое точное значение было получено при измерении ускорения свободного падения с помощью наклонной плоскости (оно равно приблизительно 9,8 м/с 2 ). Несмотря на некоторые погрешности в измерениях, можно сказать, что ускорение свободного падения является постоянной величиной. Таким образом, я добилась поставленных цели и задач.

Источник

Измерение ускорения свободного падения на различных высотах при помощи математического маятника

1. Введение

Первым человеком, изучавшим природу падения тел, был греческий ученый Аристотель. Затем Галилео Галилей обобщил и не проанализировал опыт и эксперименты нескольких поколений исследователей. Он предположил, что в среде, свободной от воздуха, все тела будут падать с одинаковой скоростью. Также Галилей предположил, что во время падения скорость тел постоянно увеличивается. Экспериментировать со свободным падением тел продолжил Исаак Ньютон. В его выводах прослеживается мысль, что на Луне и на других планетах сила тяжести, воздействующая на одно и то же тело, будет неодинакова, зависит она напрямую от массы космического тела. Например, ускорение g на Луне в несколько раз меньше, чем на Земле. Таким образом, зная массу планеты, можно вычислить ускорение свободного падения тела на этой планете.

Цель настоящего исследования состояла в получении значения ускорения свободного падения при помощи математического маятника в условиях разного уровня высоты на уровнем моря. Для достижения поставленной цели были сформулированы следующие задачи исследования:

1. Ознакомиться с историей открытия свободного падения тел;
2. Изучить методы измерения ускорения свободного падения на поверхности Земли;
3. Провести самостоятельные измерения ускорения свободного падения при помощи математического маятника;
4. Провести измерения на различных высотах.

Гипотеза исследования: логично предположить, что ускорение свободного падения, полученные в разных экспериментах, должны быть близки к значению 9,8 м/с 2 и отличаться на сотые или тысячные доли на глубине станции метро Кремлевская (–34 м) и на высоте небоскреба «Лазурные небеса» (+120 м). Также результаты измерений и вычислений могут отличаться погрешностью измерений.

Методы изучения: самостоятельная, индивидуальная работа в сочетании с теоретическими исследовательскими, проектными формами работы.

Читая много различной в том числе и технической литературы, я узнал о практическом применении различия ускорения свободного падения в разных точках на поверхности Земли. Я измерял g различными способами, рассчитывал погрешности измерений, опираясь на общепринятое значение g, учился грамотно проводить эксперимент. Выяснил, что свободное падение – движение равноускоренное. Ускорение свободного падения не зависит от массы тела. Гипотезу о том, что значения ускорения свободного падения должны быть близки к значению 9,8 м/с 2 и отличаться только погрешностью измерений удалось подтвердить разными экспериментами. Наиболее точный результат ускорения свободного падения у меня получился с помощью математического маятника. Поэтому для исследования изменения значения ускорения свободного падения с высотой я выбрал именно этот способ измерения. Погрешность составила не более 10%.

В дальнейшем я хотел бы самостоятельно исследовать зависимость значения ускорения свободного падения от географического положения.

2. Основная часть

2.1. Исторические сведения об открытии свободного падения и методах его измерения

Еще тысячелетия назад люди замечали, что большая часть предметов падает все быстрее и быстрее, а некоторые падают равномерно. Но как именно падают эти предметы – этот вопрос первобытных людей не занимал. Тем не менее нашлись люди, которые по мере возможностей начали исследовать это явление. Сначала они проделывали опыты с двумя предметами. Например, брали два камня, и давали возможность им свободно падать, выпустив их из рук одновременно. Затем снова бросали два камня, но уже в стороны по горизонтали. Потом бросали один камень в сторону, и в тот же момент выпускали из рук второй, но так, чтобы он просто падал по вертикали. Люди извлекли из таких опытов много сведений о природе. Из опытов с падающими телами люди установили, что маленький и большой камни, выпущенные из рук одновременно, падают с одинаковой скоростью. То же самое можно сказать о кусках свинца, золота, железа, стекла, и т.д. самых разных размеров. Из подобных опытов выводиться простое общее правило: свободное падение всех тел происходит одинаково независимо от размера и материала, из которого тела сделаны. Между наблюдением за причинной связью явлений и тщательно выполненными экспериментами, вероятно, долго существовал разрыв. Две тысячи лет назад некоторые древние ученые, по-видимому, проводили вполне разумные опыты с падающими телами. Великий греческий философ и ученый Аристотель, по-видимому придерживался распространенного представления о том, что тяжелые тела падают быстрее, чем легкие. Аристотель и его последователи стремились объяснить, почему происходят те или иные явления, но не всегда заботились о том, чтобы пронаблюдать, что происходит и как происходит. Он говорил, что тела стремятся найти свое естественное место на поверхности Земли. В XIV столетии группа философов из Парижа восстала против теории Аристотеля и предложила значительно более разумную схему, которая передавалась из поколения в поколение и распространилась до Италии, оказав двумя столетиями позднее влияние на Галилея. Парижские философы говорили об ускоренном движении и даже о постоянном ускорении, объясняя эти понятия архаичным языком. Великий итальянский ученый Галилео Галилей обобщил имеющиеся сведения и представления и критически их проанализировал, а затем описал и начал распространять то, что считал верным. Галилей понимал, что последователей Аристотеля сбивало с толку сопротивление воздуха. Он указал, что плотные предметы, для которых сопротивление воздуха несущественно, падают почти с одинаковой скоростью.

Предположив, что произошло бы в случае свободного падения тел в вакууме, Галилей вывел следующие законы падения тел для идеального случая: все тела при падении движутся одинаково; начав падать одновременно, они движутся с одинаковой скоростью; движение происходит с «постоянным ускорением»; темп увеличения скорости тела не меняется, т.е. за каждую последующую секунду скорость тела возрастает на одну и ту же величину. Существует легенда, будто Галилей проделал большой демонстрационный опыт, бросая легкие и тяжелые предметы с вершины Пизанской падающей башни (одни говорят, что он бросал стальные и деревянные шары, а другие утверждают, будто это были железные шары весом 0,5 и 50 кг). Описаний такого публичного опыта нет, и Галилей, несомненно, не стал таким способом демонстрировать свое правило. Галилей знал, что деревянный шар намного отстал бы при падении от железного, но считал, что для демонстрации различной скорости падения двух неодинаковых железных шаров потребовалась бы более высокая башня. Итак, мелкие камни слегка отстают в падении от крупных, и разница становится тем более заметной, чем большее расстояние пролетают камни. И дело тут не просто в размере тел: деревянный и стальной шары одинакового размера падают не строго одинаково. Галилей знал, что простому описанию падения тел мешает сопротивление воздуха. Но он мог лишь уменьшить его и не мог устранить его полностью. Поэтому ему пришлось вести доказательство, переходя от реальных наблюдений к постоянно уменьшающимся сопротивлением воздуха к идеальному случаю, когда сопротивление воздуха отсутствует. Позже, оглядываясь назад, он смог объяснить различия в реальных экспериментах, приписав их сопротивлению воздуха.

Вскоре после Галилея были созданы воздушные насосы, которые позволили произвести эксперименты со свободным падением в вакууме. С этой целью Ньютон выкачал воздух из длинной стеклянной трубки и бросил сверху одновременно птичье перо и золотую монету. Даже столь сильно различающиеся по своей плотности тела падали с одинаковой скоростью. Именно этот опыт дал решающую проверку предположения Галилея. Опыты и рассуждения Галилея привели к простому правилу, точно справедливому в случае свободного падения тел в вакууме. Это правило в случае свободного падения тел в воздухе выполняется с ограниченной точностью. Поэтому верить в него, как в идеальный случай нельзя. Для полного изучения свободного падения тел необходимо знать, какие при падении происходят изменения температуры, давления, и др., то есть исследовать и другие стороны этого явления. Так Галилей установил признак равноускоренного движения:

Таким образом, можно предположить, что свободное падение есть равноускоренное движение. Так как для равноускоренного движения перемещение рассчитывается по формуле, то если взять три некоторые точки 1,2,3 через которые проходит тело при падении и записать: (ускорение при свободном падении для всех тел одинаково), получится, что отношение перемещений при равноускоренном движении равно:

Остается еще добавить небольшой комментарий относительно экспериментов со свободным падением тел Исаака Ньютона. В его выводах прослеживается мысль, что на Луне и на других планетах сила тяжести, воздействующая на одно и то же тело, будет неодинакова, зависит она напрямую от массы космического тела. Например, ускорение g на Луне в несколько раз меньше, чем на Земле. Таким образом, зная массу планеты, можно вычислить ускорение свободного падения тела на этой планете.

2.2. Практическая значимость нахождения значения ускорения свободного падения

Я много читаю и, как следствие склонен фантазировать. Для меня практическая значимость исследования заключается в возможности прогнозирования форм жизни на небесных телах, с которыми человечество столкнется при неизбежном освоении космоса. Ведь от значения g на другой планете зависит не только сила тяжести. Люди заранее смогут узнать, какие существа встретят их на той или иной планете, какими физическими характеристиками они будут обладать.

2.3. Методы измерения ускорения свободного падения

На самом деле методов по измерению ускорения свободного падения достаточно много. Приведу только те, которые сам испробовал.

1) Измерение ускорения свободного падения с помощью наклонной плоскости

Понадобится следующее оборудование:деревянный брусок, трибометр, штатив с муфтой и лапкой, электронный секундомер, динамометр, измерительная лента, линейка. Рассматривая движение бруска вниз по наклонной плоскости, можно записать второй закон Ньютона в векторном виде:

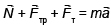
Записывая второй закон Ньютона в проекциях на оси координат:

и учитывая, что N = mgcos α ; F_тр = μN; можно решить данную систему уравнений и получить ускорение свободного падения:

g =	a
	sin α – μcos α

При этом ускорение a можно вычислить из формулы

S =	a t 2	,
	2

так как начальная скорость бруска при скольжении по наклонной плоскости равна 0:

a =	2S	.
	t 2

Видим, что для этого нужно измерить длину наклонной плоскости и время скольжения по ней бруска.

Для вычисления sinα и cosα нужно знать длину S и высоту h наклонной плоскости:

sin α =	h
	S

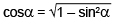
Для определения коэффициента трения скольжения положим трибометр на горизонтальную поверхность и с помощью динамометра равномерно протащим по нему брусок. В этом случае на брусок будут действовать 4 силы: сила тяжести, сила упругости пружины динамометра, сила трения, сила реакции опоры.

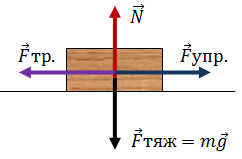
При равномерном движении бруска эти силы будут попарно равны: F_тр = F_упр, F_тяж = N, т. е. F_упр = μF_тяж, тогда коэффициент трения равен

μ =	Fy
	Fт

Для меня в этом методе оказалось слишком много математических действий, с которыми в курсе математики я еще не знаком. Поэтому даже не буду приводить результаты проделанных измерений и вычислений.

2) Определение g благодаря давлению жидкости

Как известно давление столба жидкости обусловлено следующими факторами: плотность жидкости, непосредственно высота столба жидкости и само значение ускорения свободного падения на данной планете.

Если преобразовать формулу P = ρ gh, получится формула нахождения g. Эта формула выглядит так g = P / ρ h, где Р – давление в жидкости на глубине h, которое можно узнать с помощью манометра, ρ – плотность воды равное 1000 кг/м 3 .

При подобных измерениях нужно учитывать погрешность измерительного прибора, манометра. Достаточно точного мне найти не удалось, поэтому для своих исследований я выбрал другой метод.

3) Измерение ускорения свободного падения с помощью математического маятника

Необходимое оборудование: секундомер, штатив с муфтой и лапкой, шарик на нерастяжимой нити, измерительная лента. При малых размерах шарика по сравнению с длиной нити и небольших отклонениях (до 10°) от положения равновесия период колебаний равен периоду колебаний математического маятника

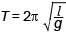
С другой стороны период колебаний маятника можно расчитать из определения, ведь период – это время одного полного колебания. Тогда период

T =	t	,
	N

и ускорения свободного падения может быть вычислено по формуле

g = 4 π 2	l N 2	.
	t 2 cр

Подготовка к проведению работы

В работе используется простейший маятник – шарик на нити. При малых размерах по сравнению с длиной нити и небольших отклонениях от положения равновесия период колебаний равен периоду колебаний математического маятника

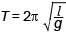
T =	t	,
	N

и ускорения свободного падения может быть вычислено по формуле

g = 4 π 2	l N 2	.
	t 2 cр

Результаты измерений и вычислений представлены в разделе 2.5

2.4. Теоретические расчеты по определению ускорения свободного падения различных высотах

Теоретически значение ускорения свободного падения на поверхности планеты Земля можно приблизительно подсчитать, представив планету точечной массой M, и вычислив гравитационное ускорение на расстоянии её радиуса R:

g = G	M	,
	R 2

где G — гравитационная постоянная (G = 6,6743 · 10 –11 (H ·м 2 )/кг 2 ).

При вычислениях я применял такие значения:

R = 6370 · 10 3 м – радиус Земли на широте Казани;

M = 5,9722 · 10 24 кг – масса Земли.

Таким образом теоретическое значение g_т = 9,823386 м/с 2 .

g = G	M	,
	(R ± h) 2

естественно предположить, что ускорение свободного падения на разных высотах будет немного отличаться: на глубине будет больше, а на высоте меньше вычисленного выше.

Возможно эту небольшую разницу можно объяснить погрешностью измерений. Проверим.

Результаты вычислений значения ускорения свободного падения на различных высотах представлены в таблице:

На станции метро Кремлевская

На 36-м этаже небоскреба

2.5. Экспериментальное определение ускорения свободного падения с помощью математического маятника

Как уже говорилось ранее, оборудование для проведения измерений требовалось весьма не замысловатое: секундомер, штатив с муфтой, шарик на нерастяжимой нити, измерительная лента. При малых размерах шарика по сравнению с длиной нити и небольших отклонениях (до 10°) от положения равновесия период колебаний равен периоду колебаний математического маятника

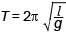
С другой стороны период колебаний маятника можно расчитать из определения, ведь период – это время одного полного колебания. Тогда период

T =	t	,
	N

и ускорения свободного падения может быть вычислено по формуле

g = 4 π 2	l N 2	.
	t 2 cр

Ход работы

Для начала я проделал все необходимые измерения в классе, в кабинете физики Лицея № 110. Кабинет находится на втором этаже. Учитывая высоту потолков (около 3 м), логично предположить, что вычисленные значения g должны быть близки к gт.

Источник