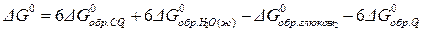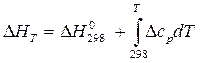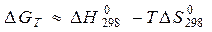Изменение энергии Гиббса в химических реакциях
Расчет DG для химических процессов можно осуществить двумя способами. В первом способеиспользуется соотношение (27):
Рассмотрим в качестве примера расчет DG 0 для реакции
Символ « 0 » , как и прежде, указывает на стандартное состояние всех участников реакции. (Как вводилось у нас ранее, стандартное состояние?)
Известно, что стандартная энтальпия образования воды равна:
Используя табличные значения стандартных энтропий участников реакции, выраженных в энтропийных единицах, э.е. (Дж/моль К),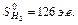 
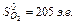
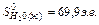
, вычислим DS 0 , используя уравнение (23):
Таким образом, найдем, что
Полученная отрицательная величина говорит о том, что в стандартных условиях эта реакция должна идти слева направо.
Во втором способе расчета DG химических реакций используют то, что эту величину можно рассчитать по известным величинам DG других реакций, комбинация уравнений которых дает интересующее нас уравнение реакции (аналогично расчету тепловых эффектов реакции). При этом мы исходим из свойств этой функции как функции состояния: считаем DG независимым от пути проведения процесса.
Наиболее удобно использовать для этих целей DG реакций образования (DGобр.). С реакциями образования мы знакомились, когда изучали 1-ое следствие из закона Гесса. Напоминаем, что реакциями образования в термодинамике считаются такие реакции, в которых 1 моль вещества в стандартном состоянии при данной температуре образуются из простых веществ, взятых в их стандартном состоянии при той же температуре. Реакции образования часто бывают гипотетическими (т.е. не идущими реально), а лишь соответствующими приведенному выше определению. В термодинамических таблицах приводятся изменения энергии Гиббса для реакций образования при стандартных условиях (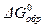 
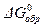
). Понятно, что 
простых веществ равно нулю.
Используя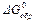 
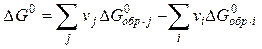
, можно рассчитать стандартное изменение энергии Гиббса (DG 0 ) любой химической реакции. Эта величина равна разности стандартных энергий Гиббса для реакций образования продуктов и исходных веществ с учетом стехиометрических коэффициентов:
(28)
В качестве примера рассчитаем (DG 0 ) важного биохимического процесса — реакции окисления глюкозы:
DG 0 = 6 (— 396,9) + 6 (— 238,1) – 913,1 = — 2885,2 кДж/моль
В биологических системах такое большое количество энергии освобождается не сразу, а небольшими порциями в сложном ряду химических превращений.
Для расчета изменения энергий Гиббса реакций при температурах, отличающихся от стандартных, DGТ, надо знать величины теплоемкостей участников реакции в интервале температур от 298К до Т. Расчетные соотношения получают следующим образом:
Так как в соответствии с уравнениями (11а) и (24)
,
(29а)
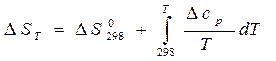
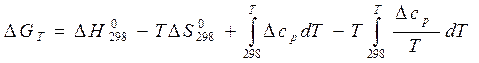
Аналогичным образом можно получить выражение зависимости DF от температуры:
(30)
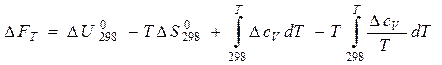
Для практического использования функций DF и DG полезно знать ответы на следующие вопросы:
1. Каковы различия между DF и DG химических реакций при T = соnst?
Из определений DF и DG следует, что
В реакциях в конденсированных средах (твердых и жидких) обычно изменением объема можно пренебречь (DV=0). Тогда
Если в реакциях участвуют газы и можно считать их идеальными, то
При Dn=0, т.е. когдареакция идет без изменения числа молей,
2. Какие выводы можно сделать, получив значения термодинамических критериев возможности самопроизвольного протекания процессов?
Если термодинамика дает отрицательный ответ на вопрос о возможности самопроизвольного протекания процесса (DF>0 или DG>0), это означает, что без внешнего подвода энергии процесс невозможен. Процесс может самопроизвольно протекать только в обратном направлении.
Если термодинамика дает положительный ответ (DF 0 = — 395,9 кДж/моль. Но графит с кислородом при 298К и р = 1 атм не реагирует. Чтобы процесс шел, необходимо создать условия для увеличения скорости (запал, катализаторы и т.д.).
3. Может ли идти процесс, если DF>0 или DG>0?
Может, но не самопроизвольно. Для его проведения надо затратить энергию. Пример − процесс фотосинтеза, идущий в растениях под воздействием солнечной энергии. Другой пример − протекание реакций, характеризующихся DG>0, при сопряжении их с реакциями, для которых DG 0 = 21 кДж/моль и, следовательно, прямая реакция самопроизвольно протекать не может. Вместе с тем, известно, что в организмах этот процесс происходит. Сопряженной реакцией в этом случае является гидролиз аденозинтрифосфата (АТФ) с образованием АДФ и фосфорной кислоты (Ф):
АТФ + Н2О ® АДФ + Ф; DG 0 = − 50,4 кДж/моль
Так как изменение G является величиной аддитивной, суммарный процесс можно записать в виде суммы двух стадий:
АТФ + глюкоза + фруктоза = сахароза + АДФ +Ф; DG 0 = − 29,4 кДж/моль
Сопряжение осуществляется путем образования в качестве промежуточного соединения глюкозо-1-фосфата. Реакция идет в 2 стадии:
(1 стадия): АТФ + глюкоза ® глюкозо-1-Ф + АДФ; DG 0 = − 29,4 кДж/моль
(2 стадия): Глюкозо-1-Ф + фруктоза ® сахароза + Ф; DG 0 = 0
Такое сопряжение типично для многих биологических реакций.
В живых организмах освобожденная при окислении глюкозы энергия не сразу расходуется в различных процессах жизнедеятельности, а запасается впрок в различных соединениях, богатых энергией, каких как эфиры фосфорной кислоты (АТФ, АДФ, креатин- и аргининфосфаты и др.).
4. В каких случаях DН (или DU) является критерием самопроизвольности процесса?
В общем случае критерием самопроизвольности является величина DG (или DF)процесса.
Т.к. DG = DH – TDS (или DF = DU – TDS), то при DS=0 (в изоэнтропийных условиях) DG = DH (или DF = DU). В этом случае DН (или DU) является критерием самопроизвольности процесса. При этом самопроизвольно идут экзотермические реакции (DH 0), т.е. процессы, связанные с разложением веществ, их деструкцией, дезагрегаций.
6. Каковы условия самопроизвольного протекания экзотермических реакций (DH 0, то DG = DH – TDS 0. Процесс не идет слева направо.
Таким образом, экзотермические реакции термодинамически запрещены только при значительном уменьшении энтропии, например, в некоторых процессах структурирования, образования дополнительных связей и т.д.
Еще один важный выход из этих рассуждений: в изолированных системах самопроизвольно могут идти процессы с уменьшением энтропии, если они сопровождаются значительным тепловым эффектом. Это особенно важно для понимания возможности самопроизвольного усложнения систем, например, в процессе роста живых организмов. В этом случае источником энергии могут являться все те же богатые энергией эфиры фосфорной кислоты (АТФ, АДФ, креатин- и аргининфосфаты и др.). Кроме того, при рассмотрении реальных систем следует иметь в виду, что они практически не бывают изолированными, и имеется возможность подачи энергии извне.
7. Каковы условия самопроизвольного протекания эндотермических реакций (DH>0),
Выберем для определенности изобарные условия протекания эндотермических реакций: DH>0. При этом возможность условия самопроизвольного протекания реакции определяется знаком DG = DH – TDS
Как и в предыдущем случае, рассмотрим, как меняется знак DG при варьировании величины DS.
а) Если DS>0, то DG = DH – TDS может иметь различные знаки в зависимости от абсолютной величины TDS:
· DH TDS. При этом DG>0. Процесс не идет самопроизвольно слева направо.
б) Если DS=0, то DG = DH – TDS>0. Процесс не идет самопроизвольно слева направо.
в) Если DS 0. Процесс не идет самопроизвольно слева направо.
Таким образом, эндотермические реакции идут самопроизвольно только при значительном увеличении энтропии в реакции, например, в процессах разложения, деструкции, дезагрегации.
8. Как влияет повышение температуры на DU, DH, DS, DG и DF химических реакций?
а) Зависимость DU от температуры выражается уравнением Кирхгоффа (14а):
.
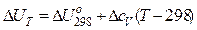
С ростом температуры величина DU растет при DсV>0 и падает при DсV 0 и падает при Dср 0 и падает при Dср 0. При DS=0 величина DF не зависит от температуры.
д) Зависимость DG от температуры выражается уравнением (29а):
.
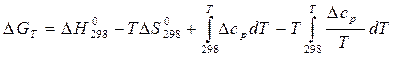
Часто можно пренебречь двумя последними слагаемыми из-за их меньшей величины по сравнению с первыми двумя слагаемыми:
Приближенно можно заключить, что с ростом температуры DG растет при DS 0. При DS=0 величина DG не зависит от температуры.
Источник
Энергию Гиббса химической реакции можно рассчитать двумя способами
ХИМИЧЕСКАЯ ТЕРМОДИНАМИКА
Система – совокупность тел, мысленно или фактически обособляемых из окружающей среды
Состояние системы характеризуется набором термодинамических параметров состояния: Т, р ,V, С …
Процесс перехода из одного состояния в другое (Т = const– изотермический, p = const— изобарический, V = const— изохорический )
ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ СОСТОЯНИЯ СИСТЕМЫ:
U-внутренняя энергия, H – энтальпия , S — энтропия, G – свободная энергия Гиббса,
F – энергия Гельмгольца
Функции состояния системы (характеристические ф-ции) свойства системы, значения которых однозначно определяются параметрами состояния. Изменение функций состояния не зависит от пути перехода системы из одного состояния в другое, а определяется лишь разностью значений функции в конечном и начальном состоянии. Величина функции зависит от количества или массы вещества.
U-внутренняя энергия— включает в себя все виды энергии системы (движения и взаимодействия молекул, атомов, ядер, электронов и др. частиц), кроме потенциальной и кинетической энергии движения всей системы как целого объекта. Абсолютное значение U определить невозможно, можно определить изменение ΔU= U2 – U1 с помощью работы (W) и теплоты (Q).
Работа (W) – количественная мера направленного движения частиц
Теплота (Q) – количественная мера хаотического движения частиц
Н=U+p·V — энтальпия, функция состояния системы, абсолютное значение определить невозможно, можно определить ΔH
Термохимия– часть термодинамики, изучающая тепловые эффекты процессов
Термохимические уравнения (указаны агрегатные состояния веществ и тепловой эффект
реакции, допустимы дробные стехиометрические коэффициенты)
Эндотермическая реакция-реакция с поглощением теплоты,ΔrH > 0 .
Экзотермическая реакция-реакция с выделением теплоты,ΔrH 5 Па
∆fH º i – стандартная энтальпия (теплота) образования
i –го вещества равна тепловому эффекту образования одного моля этого вещества из соответствующих простых веществ, если все участники реакции находятся в стандартных состояниях При этом энтальпии образования простых веществ, устойчивых в данных условиях, принимают равными нулю.
Тогда стандартная энтальпия реакции равна:
Стандартные энтальпии образования табулированы, как правило, при 298 К (Δf Hº298)
Зависимость энтальпии реакции (в данном случае стандартной) от температуры в области 298 ÷Т, в которой нет фазовых переходов, в интегральномвиде выражается уравнением Кирхгофа:
Δr HºT= Δr Hº298+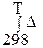 
rcºpdT
Где ∆rcºp – изменение стандартной теплоемкости системы в ходе реакции, равное разности суммарной стандартной теплоемкости продуктов реакции и суммарной стандартной теплоемкости исходных веществ с учетом стехиометрических коэффициентов
Энтропия S –функция состояния системы мера неупорядоченности состояния системы
S=R·lnW (W-термодинамическая вероятность системы, число возможных микросостояний, которыми можно реализовать данное макросотояние) [дж/моль·К]. Можно определить абсолютное значение (3-ий закон термодинамики- энтропия идеального кристалла при Т= 0 К равна 0). Энтропия увеличивается с ↑Т ; Sг>Sж>Sт
Стандартную энтропию реакции при 298К, ∆rSº298 рассчитывают по формуле
Зависимость энтропии реакции от температуры в области 298 ÷Т, в которой нет фазовых переходов, в интегральном виде выражается уравнением:
∆rSºТ = ∆rSº298+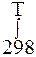 
(∆r cºp /Т)dT Если ∆rcºp=0 , то ∆r SºT= ∆r Sº298
Функциями состояния системы: энергия Гиббса: G=Н-T·S, и энергия Гельмгольца: F=U-T∙S
Критерий возможности самопроизвольного протекания реакции в прямом направлении в изобарно-изотермических условиях:∆rGТ=∆rНТ — Т∙∆rSТ º
Энергию Гиббса химической реакции можно рассчитать двумя способами
Если исходные вещества и продукты реакции находятся в стандартных состояниях, то по этим формулам рассчитывают стандартную энергию Гиббса реакции ∆rGºT. Связь между ∆rGT (при нестандартных состояниях веществ) и∆rGºT (при стандартных)
выражается уравнением изотермы Вант-Гоффа
где pi – относительное парциальное давлениесоответствующих газообразных компонентов реакции
Источник
