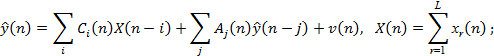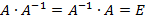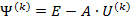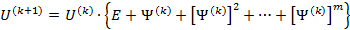Применение итерационного алгоритма Шульца в рекуррентных алгоритмах параметрической идентификации
Рубрика: Технические науки
Дата публикации: 30.10.2014 2014-10-30
Статья просмотрена: 1151 раз
Библиографическое описание:
Куроткин, В. А. Применение итерационного алгоритма Шульца в рекуррентных алгоритмах параметрической идентификации / В. А. Куроткин. — Текст : непосредственный // Молодой ученый. — 2014. — № 18 (77). — С. 251-255. — URL: https://moluch.ru/archive/77/13348/ (дата обращения: 23.11.2021).
В данной статье рассмотрен процесс исследования и реализации рекуррентных алгоритмов параметрической идентификации (на примере алгоритма Левенберга-Маркварда) в программной среде Unity Pro XL с использованием средств промышленной автоматики, в том числе — программируемых логических контроллеров Schneider Electric. В частности, в статье приведена разработка алгоритма итерационного поиска обратной матрицы с применением алгоритма Шульца.
Ключевые слова:параметрическая идентификация, рекуррентные алгоритмы идентификации, итерационного алгоритма Шульца, ПЛК, Schneider Electric.
В настоящее время предложено достаточно много методов и алгоритмов идентификации [1–4]. Большинство из них основано на методе наименьших квадратов и его модификациях. В условиях неопределённости широкое применение получили итерационные методы, обладающие рядом преимуществ: простота реализации, большое быстродействие, возможность получения состоятельных оценок. Некоторые конструктивные особенности в итерационные алгоритмы вносятся в процессе непосредственной реализации их в системах управления программируемых логических контроллеров (ПЛК), что связано с особенностями и свойствами исследуемого процесса или объекта.
Алгоритмы рекуррентной параметрической идентификации
Практически все рассматриваемые алгоритмы рекуррентной параметрической идентификации представляют собой нелинейные функции, поэтому получение аналитических оценок для большинства алгоритмов вызывает значительные трудности. Кроме того, для практических приложений важными являются такие параметры модели объекта, как высокий порядок дифференциального или разностного уравнения и произвольное количество входов. Поэтому сравнение алгоритмов выполнялось численным моделированием. Для получения достоверных убедительных результатов на основе численного моделирования необходимо с одной стороны иметь возможность получать достаточно разнообразные входные сигналы и возможность рассматривать различные типы параметрической нестационарности. С этой целью был создан программный пакет в среде Unity Pro XL v7.0 фирмы Schneider Electric, позволяющий выполнить поставленную задачу. В программном пакете предусмотрено моделирование входных сигналов по вероятностным распределениям: равномерное, нормальное, гамма, бета, экспоненциальное, Лапласа, Коши. Реализованы алгоритмы идентификации коэффициентов в авто регрессионном уравнении [1–5]: алгоритмы на основе P- и SP- подходов, алгоритмы Айзермана, Качмажа, Нагумо-Нода, МНК, РМНК, Аведьян, Растригин, алгоритмы Цыпкина, фильтр Калмана, алгоритм Фактор забывания, алгоритм Левенберга-Маркварда.
Схема адаптивной системы управления с идентификатором представлена на рис 1. В исследуемой системе под объектом идентификации, подразумевалась модель технологического процесса, которая описывается как многомерный односвязный объект с наблюдаемыми входами и выходом [5]:
Где 
— шаг идентификации, 
— статические параметры объекта управления, 
— динамические параметры объекта управления, 
— вектор наблюдаемых входов, 
— входы модели объекта управления (
), 
— количество входов, 
— выход модели объекта управления, 
— приведенный аддитивный шум.
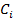
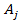
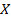
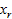
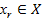
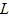
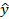
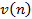
Рис. 1. Адаптивная система с идентификатором.
В рассматриваемой адаптивной системе (рис. 1) исследовалось применение различных рекуррентных алгоритмов в блоке идентификации. В частности, рассматривалось использование алгоритма Левенберг-Маркварда, как одного из наиболее эффективных.
В теории автоматического управления алгоритма Левенберг-Маркварда [2] (в векторной форме) для подстройки коэффициентов модели объекта управления выглядит следующим образом:
,
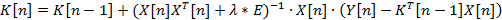
Где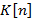 
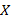
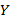
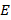
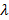
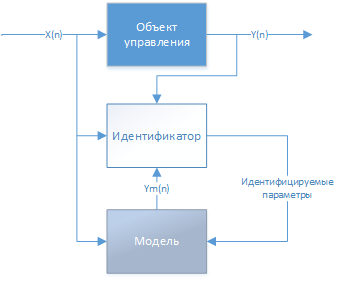
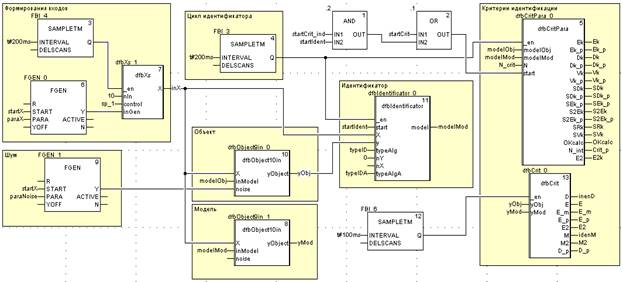
— идентифицируемые статические и динамические параметры (
), 
— шаг идентификации, 
— вектор входов, 
— вектор выходов, 
— единичная матрица, 
— константа идентификации.
На рис.3 приведен пример реализации алгоритмов идентификации на языке функциональных блоков стандарта МЭК 61131–3 в программной среде Unity.Pro [7]. На рис.4 представлен тренд работы алгоритма идентификации — реальные и идентифицируемые параметры.
Рис. 2. Пример реализации алгоритмов идентификации в программной среде Unity.Pro.
Рис. 3. Параметры объекта (вертикальные тренды) и параметры модели.
Способы нахождения обратной матрицы
Как представлено выше, алгоритмы идентификации содержат требование нахождения обратной матрицы. Обратная матрица — это такая матрица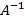 
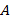
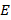
, при умножении на которую исходная матрица 
даёт в результате единичную матрицу :
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. В представленных выше алгоритмах идентификации поиск обратной матрицы осуществляется у заведомо квадратной матрицы (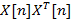
). Существуют точные (прямые) методы нахождения обратных матриц [6]:
— Метод Гаусса—Жордана. Сложность алгоритма —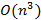 
.
— С помощью матрицы алгебраических дополнений. Сложность алгоритма зависит от сложности алгоритма расчета определителя и равна —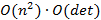 
.
— Использование LU/LUP-разложения. Сложность алгоритма — .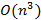
Итерационные методы нахождения обратных матриц:
— Итерационный метод Шульца. Зависит от матрицы начального приближения. Сложность алгоритма —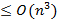 
.
Поскольку рассматриваемые в этой статье алгоритмы идентификации обладают свойством рекуррентности и вычисляются итерационно — что наиболее удобно в программировании ПЛК и работе в режиме реального времени, то использование итерационного метода Шульца наиболее удобен в решение задачи поиска обратной матрицы. Этот алгоритм представляют собой рекуррентные соотношения, осуществляя которые мы получаем все более точное приближение к обратной матрице. В алгоритмах Гаусса и LU-разложения обратная матрица получается после фиксированного числа арифметических операций. А итерационный метод Шульца зависит от матрицы начального приближения, но, этот недостаток не так значителен, поскольку в любом случае мы получаем матрицу с элементами, точность которых ограничена вычислительной погрешностью.
Итерационный метод Шульца
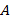
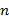
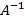
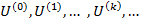
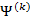
Для квадратной невырожденной матрицы порядка можно найти обратную матрицу в результате последовательных приближений. Приближения также представляют собой квадратные матрицы — 
. и имеют обратные матрицы — 
[6].
Отклонение текущего приближения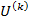 
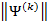
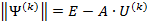
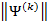
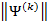
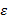
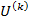
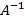
от искомой обратной матрицы можно оценивать величиной 
, где 
. Равенство нулю означает, что текущее приближение совпадает с обратной матрицей. Для оценки приближения к нулю необходимо ввести 
— малое положительное число. Доказательство сходимости последовательности матриц к представлено в теореме о сходимости итерационного метода Шульца [].
Порядок действий при вычислении итерационного метода Шульца:
1) Присвоить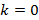 
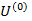
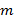
. Задать 
— начальное приближение обратной матрицы; 
— порядок метода.
2) Вычислить 
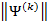
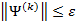
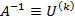
3) Вычислить . Если 
, обратная матрица найдена 
. Иначе перейти к пункту 4.
4) Найти следующее приближение по формуле:
a. 
5) 
и перейти к пункту 2.
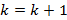
На языке структурного текста МЭК61131–3 для ПЛК в программной среде Unity Pro XL v7.0 фирмы Schneider Electric, данный алгоритм будет выглядеть следующем образом:
Источник
Итерационный метод Шульца нахождения обратной матрицы
Пусть дана квадратная невырожденная матрица [math]A[/math] порядка [math]n[/math] . Будем искать обратную матрицу [math]A^<-1>[/math] в результате последовательных приближений, обозначая эти приближения [math]U^<(0)>,U^<(1)>,\ldots,U^<(k)>,\ldots[/math] . Отклонение (невязку) текущего приближения от искомой обратной матрицы предлагается оценивать величиной [math]\bigl\|\Psi^<(k)>\bigr\|[/math] , где [math]\Psi^<(k)>= E-A\cdot U^<(k)>[/math] . Равенство невязки нулю означает, что текущее приближение совпадает с обратной матрицей.
Алгоритм итерационного метода Шульца
1. Положить [math]k=0[/math] . Задать [math]U^<(0)>[/math] — начальное приближение обратной матрицы; [math]\varepsilon[/math] — малое положительное число; [math]m[/math] — порядок метода.
2. Вычислить [math]\Psi^<(k)>= E-A\cdot U^<(k)>[/math] .
3. Вычислить [math]\bigl\|\Psi^<(k)>\bigr\|[/math] . Если [math]\bigl\|\Psi^ <(k)>\bigr\|\leqslant \varepsilon[/math] , процесс завершить и положить [math]A^<-1>\equiv U^<(k)>[/math] . Иначе перейти к пункту 4.
4. Найти следующее приближение
положить [math]k=k+1[/math] и перейти к пункту 2.
Теорема (10.4) о сходимости итерационного метода Шульца. Пусть квадратные матрицы [math]A[/math] и [math]U^<(0)>[/math] таковы, что матрица [math]U^<(0)>[/math] имеет обратную и [math]\bigl\|\Psi^<(0)>\bigr\| . Тогда существует обратная матрица [math]A^<-1>[/math] и к ней сходится последовательность матриц [math]\bigl\
1. Заданием параметра т можно получать различные итерационные процедуры, обладающие (m+1)-м порядком сходимости. Обычно полагают [math]m=1[/math] или [math]m=2[/math] . Очевидно, чем больше [math]m[/math] , тем больше порядок сходимости метода, однако при [math]m=2[/math] обеспечивается минимум вычислительных затрат, требующихся для обращения матриц с заданной точностью методами семейства (10.18).
2. Для выбора начального приближения [math]U^<(0)>[/math] существуют следующие рекомендации. Если [math]A[/math] — симметрическая положительно определенная матрица и ее спектральный радиус [math]\rho(A)\leqslant\beta[/math] , то [math]U^<(0)>=\alpha E[/math] , где [math]\alpha\in\!\left(0;\frac<2><\beta>\right)[/math] . Если [math]A[/math] — произвольная невырожденная матрица и спектральный радиус [math]\rho(AA^T)\leqslant \beta[/math] , то [math]U^<(0)>=\alpha A^T[/math] , где [math]\alpha\in\!\left(0;\frac<2><\beta>\right)[/math] . Однако надо иметь в виду, что при этом может не удовлетворяться условие [math]\bigl\| \Psi^<(0)>\bigr\| . Поэтому лучше задавать матрицу [math]U^<(0)>[/math] так, чтобы это условие выполнялось. Тогда алгоритм достаточно быстро сходится к искомому решению задачи.
Пример 10.18. Дана матрица [math]A=\begin
Решение. 1. Положим [math]k=0;
m=1[/math] . Зададим начальное приближение
3. Так как [math]\bigl\|\Psi^<(0)>\bigr\|_4=0,\!933 , то выполняется условие теоремы 10.4. Поскольку \varepsilon=0,\!01″>[math]\bigl\|\Psi^ <(0)>\bigr\|_4= 0,\!933> \varepsilon=0,\!01[/math] , перейдем к пункту 4.
Положим [math]k=1[/math] и перейдем к пункту 2. Далее процесс продолжается. Приведем результаты на последующих итерациях:
Поскольку [math]\bigl\|\Psi^<(4)>\bigr\|_4=4,\!836\times10^ <-3>, процесс завершается и в качестве приближенного решения задачи принимается [math]A^<-1>\cong U^<(4)>[/math] . Найденный результат практически совпадает с полученным в примере 4.3
Источник
