Старинные способы умножения и деления
В работе рассмотрены несколько способов умножения: крестьянский ( удвоение). умножение на пальцах от 6 до 9, египетский, умножение решеткой, а также два способа деления : галерой и методом Гилберта. Сделаны сравнительные выводы о достоинствах и недостатках указанных методов с о школьными общепринятыми.
Скачать:
| Вложение | Размер |
|---|---|
| starinnye_sposoby_umnozheniya_i_deleniya.docx | 418.64 КБ |
Предварительный просмотр:
Муниципальный конкурс научно-исследовательских и творческих работ «Первые шаги в науке»
СЕКЦИЯ ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, МАТЕМАТИКА;
Cтаринные способы умножения и деления
Автор Автомонов Денис,
ученик 7А класса
Айзикович Анна Георгиевна,
МБОУ «СОШ № 13 с углублённым
изучением отдельных предметов»
г.Губкина Белгородской области
Можно ли представить мир без чисел? Без чисел ни покупки не сделаешь, ни времени не узнаешь, ни номера телефона не наберёшь. А космические корабли, лазеры и все другие технические достижения?! Они были бы попросту невозможны, если бы не наука о числах.
Две стихии господствуют в математике — числа и фигуры с их бесконечным многообразием свойств и действий с ними. В современном мире математическая грамотность является одной из основных целей образования. Она включает в себя, в частности, умение совершать арифметические действия, проводить подсчёты и измерения.
Подсчитывать предметы люди научились ещё в древнем каменном веке — палеолите, десятки тысяч лет назад. Как это происходило? Сначала люди лишь на глаз сравнивали разные количества одинаковых предметов. Чтобы с успехом заниматься сельским хозяйством, понадобились арифметические знания. Без подсчета дней трудно было определить, когда надо засевать поля, когда начинать полив, когда ждать потомства от животных. Надо было знать, сколько овец в стаде, сколько мешков зерна положено в амбары.
Практическая сторона арифметики включает в себя методы, схемы и алгоритмы для осуществления точных арифметических действий, в том числе использование счётных машин. В школе изучают таблицу умножения, а затем учат детей умножать числа в столбик. Разумеется, это не единственные способы выполнения операций умножения и деления.
Гипотеза – используемые алгоритмы умножения и деления натуральных чисел — не единственные.
Проблема – просты ли наши современные способы различных вычислений, какие нестандартные приёмы умножения и деления существуют для счета?
Цель работы – рассмотреть нестандартные приёмы умножения и деления не рассматриваемые в школьном курсе математики.
- изучить соответствующую литературу,
- описать некоторые способы умножения и деления, опытным путём выявить трудности их использования,
- продемонстрировать преимущество и недостатки старинных способов умножения и деления .
Актуальность данной темы заключается в том, что использование нестандартных приемов в формировании вычислительных навыков усиливает интерес к математике и содействует развитию математических способностей. За простым действием умножения скрываются тайны истории математики. Изучение математики развивает логическое мышление, память, гибкость ума, приучает человека к точности, к умению видеть главное, сообщает необходимые сведения для понимания сложных задач, возникающих в различных областях деятельности современного человека. Для изучения данной темы, автор изучил работы таких авторов как Депнам И.Я., Виленкин Н.Я. «За страницами учебника математики» Гейзер Г.И. «История математики в школе», в которых нашел историю появления приемов арифметических операций; в энциклопедии для детей «Математика» ( серия Аванта ) были найдены старинные способы умножения и деления галерой.
Для натуральных чисел естественным образом определены операции сложения и умножения Многократное сложение элементов нескольких одинаковых множеств не зависит от порядка этих множеств, что позволило определить другую бинарную операцию — умножение. Помимо умножения, в древности существовало отдельное арифметическое действие — удвоение, или умножение на два. Обратной к операции умножения является операция деления. Первое определение деления — это поиск числа, которое содержится в делимом столько раз, сколько единиц содержится в делителе. Деление считалось очень сложной и громоздкой операцией. Современный способ деления, использующий частичные произведения делителя на отдельные разряды частного (деление столбиком), представлен в итальянском манускрипте 1460 года. Предки наши пользовались гораздо более громоздкими и медленными приемами. И если бы школьник XX века мог перенестись за четыре, за три века назад, он поразил бы наших предков быстротой и безошибочностью своих арифметических выкладок. Молва о нем облетела бы окрестные школы и монастыри, затмив славу искуснейших счетчиков той эпохи, и со всех сторон приезжали бы учиться у нового, великого мастера счетного дела.
Источник
Итальянский способ
В Италии, а также во многих странах Востока, этот способ приобрел большую известность. Он имеет название «Джелозия». Также его часто называют способом решетки.
А лгоритм решения:
1. Нарисовать прямоугольник.
2. Разделить его по одной клетке на одну цифру.
3. Над каждой клеткой подписать соответствующие цифры.
4. Поделить каждую клетку по диагонали на две части.
5. Перемножить первые знаки каждого числа.
6. В первом и втором треугольнике записать результат умножения.
7. Умножить второй знак первого числа на первый второго числа.
8. В первом и втором треугольнике записать результат умножения.
9. Перемножить вторые знаки каждого числа.
10. В первом и втором треугольнике записать результат умножения.
11. Умножить первый знак первого числа на второй знак второго числа.
12. В первом и втором треугольнике записать результат умножения.
13. Разбить прямоугольник на части.
14. Сложить числа в каждой из частей.
15. Получить результат.
Суть этого способа умножения поясним на примере.
Вычислим произведение 296 на 73. Начнем с того, что нарисуем таблицу с квадратными клетками, в которой будет три столбца и две строки, – по количеству цифр в множителях. Разделим клетки пополам по диагонали, и «…получается картинка, похожая на решетчатые ставни-жалюзи, – пишет Пачиоли. – Такие ставни вешались на окна венецианских домов, мешая уличным прохожим видеть, сидящих у окон дам и монахинь».
Над таблицей запишем число 296, а с правой стороны вертикально – число 73. Перемножим каждую цифру первого числа с каждой цифрой второго и запишем произведения в соответствующие клетки, располагая десятки над диагональю, а единицы под ней. Однозначный результат записываем под диагональю. Цифры искомого произведения получим путем суммирования чисел, записанных между диагональными линиями (в косых полосах). При этом будем двигаться по часовой стрелке, начиная с правой нижней клетки: 8, 2+1+7 и т.д. Запишем результаты под таблицей, а также слева от нее ( е сли при сложении получится двузначная сумма, укажем только единицы, а десятки прибавим к сумме цифр из следующей полосы).
Источник
Реферат на тему «»Волшебник» из Багдада»
Неудивительно, что известный историк науки Дж. Сартон назвал Аль-Хорезми величайшим математиком своего времени и, если принять во внимание все обстоятельства, одним из величайших всех времен.
Просмотр содержимого документа
«Реферат на тему «»Волшебник» из Багдада»»
«Волшебник» из Багдада 3
Математические трактаты 5
«Книга об индийском счете» 5
«Краткая книга об исчислении ал-джабры и ал-мукабалы» 7
Метод Аль-Хорезми — почти алгебраический 10
О записи числа 11
« Я 
составил краткую книгу об исчислении
алгебры и алмукабалы, заключающую в себе
простые и сложные вопросы арифметики, ибо это необходимо людям».
Аль-Хорезми Мухаммед бен-Муса (783-850)
«Волшебник» из Багдада
В рамках внеурочного курса по математике «Удивительный мир чисел» мы познакомились с выдающимся арабским математиком и астроном Абу Абдалах Мухаммед Бен Мусса аль – Хорезми. Что же это за математик из древности, незримо присутствующий на уроках математики много веков спустя?
Ответ на этот вопрос мы и попыталась найти в данной работе.
«Волшебник» из Багдада
Багдад был основан в 60-х гг. VIII в. халифом ал-Мамун-ром из династии Аббасидов, правившим с 754 по 775 год. Новая столица государства, занимавшего в то время огромную территорию, быстро стала важным центром торговли, науки и культуры. Управлять огромным государством было нелегко. Правители халифата поняли, что их экономические и военные планы нельзя воплотить в жизнь, если не будут освоены те знания, которыми владели покоренные народы. Поэтому повелители всемерно содействовали развитию науки. В Багдаде возникла крупная научная школа, которая привлекала к себе выдающихся ученых из разных стран. Была создана библиотека, пополнявшаяся ценными научными трудами. Они стали приглашать в Багдад виднейших ученых из покоренных стран.
До 813 года ал-Мамун был наместником восточных провинций и жил в Мерве. Не исключено, что здесь он и встретился с ал-Хорезми, а впоследствии пригласил его в Багдад. В одном из своих сочинений ал-Хорезми с похвалой отозвался об ал-Мамуне. Он отмечал его «любовь к науке и стремление приближать к себе ученых, простирая над ними крыло своего покровительства и помогая им в разъяснении того, что для них неясно, и в облегчении того, что для них затруднительно».
Аль-Хорезми — великий математик, астроном и географ, основатель классической алгебры. В исторических источниках нет упоминания о конкретном месте рождения Аль Хорезми, но некоторые косвенные соображения позволяют допустить, что он происходил из древней Хивы.
Полное имя ал-Хорезми — Абу Абдаллах (или Абу Джафар) Мухаммед ибн Муса ал-Хорезми. Что же скрывается под этим именем?
Арабы имеют привычку прятать в имени человека целую биографию:
Абу Абдуллах (или Абу Джафар) Мухаммед ибн Муса Аль-Хорезми -Абу — означает «Отец кого-то». Другими словами, Абу Абдуллах (или Абу Джафар) означает, что у него было как минимум два сына: Абдулла и Джафар. Мухаммед ибн Муса Аль-Хорезми — имя ученого – Мухаммед, ибн с арабского означает «Сын». Значит, отца ученого звали Муса.
Более того, теперь мы можем сразу сказать, откуда ученый был родом.
Слова «Аль-где-то» указывают, что Мухаммед Аль-Хорезми был родом из Хорезма. Ныне Хорезм — это город в Узбекистане.
Оказывается, что Узбекистан и есть то звено в «исторической цепочке», откуда к нам пришло наше современное математическое знание с ее строгой логикой.
В некоторых исторических источниках Аль-Хорезми назван «ал-маджуси», т. е. маг. Из этого заключают, что его предки были магами — жрецами зороастрийской религии, распространенной на территории Средней Азии. Это даёт повод считать, что одним из источников знаний Мухаммеда Аль-Хорезми была наука доисламской Средней Азии, хранителями которой были маги.
Биографических сведений об Аль-Хорезми история почти не сохранила. До нас не дошли даже точные даты его рождения и смерти. Известно лишь, что он родился в конце восьмого века, а умер во второй половине девятого, точнее после 847 г. Сейчас условно принято считать годом его рождения 783, а годом смерти 850 год.
Известно, что он возглавлял в Багдаде библиотеку Дома мудрости, своего рода Багдадской академии, при халифе ал-Мамуне. А при другом халифе ал-Васике, преемнике ал-Мамуна, он возглавлял экспедицию к хазарам.
Наиболее поздняя дата, связанная с именем Аль-Хорезми, — 847 год. В этом году умер халиф ал-Васик, и ал-Хорезми упоминается среди лиц, присутствовавших при его кончине.
Таким образом, мы видим, что фактов из жизни великого среднеазиатского ученого сохранилось очень мало. Поэтому историки науки основываются главным образом на исследовании его трудов.
В 975-997 он написал Mafatih al-‘Ulum («Ключ к Наукам»), первая арабская энциклопедия знаний, которая была организована на научных принципах. Ее содержание было классифицировано:
местные знания — юриспруденция, схоластическая философия, грамматика, секретарские обязанности, просодия и поэтическое искусство, история;
иностранные знания — философия, логика, медицина, арифметика, геометрия, астрономия, музыка, механика, алхимия.
Как ученый Ал-Хваризми становится известным из его достижений в математике. Его работа над арифметикой была переведена на латинский в 12-ом столетии, и хотя оригинал потерян, латинский перевод Algoritmi de numero Indorum («Ал-Хваризми о индийских числах») все еще существует. Его название давало начало математическому термину «арифметика».
Другая работа Ал-Хваризми, Kitab al-jabr wa l-muqabala («Книга Интеграции и Уравнения, » буквально «сокращение и сравнение»), был синтез индийской алгебры и греческой геометрии и имел самый глубокий эффект на развитие науки. Латинские переводы, резюме и комментарии были написаны в 12 столетии. Математический термин «алгебра» был получен из ее названия.
Оба математических трактата служили долгое время основными учебниками по математики. Остановимся более подробно на них.
«Книга об индийском счете»
В «Книге об индийском счёте» Мухаммед ибн Мусса подробно описал правила, по которым надо выполнять арифметические действия. Некоторые из них были похожи на применяемые сейчас. Например, сложение и вычитание столбиком.
А вот правила умножения и деления были иными. Для умножения чисел Аль-Хорезми предлагал «метод решетки», в некотором роде проще, чем применяемый в школе. Пусть надо умножить 347 на 29. Начертим таблицы:
Таблица 1. Умножение Таблица 2. Умножение по разрядам
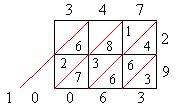
Над Таблицей 1 надпишем 347 слева направо, а справа от неё – число 29 сверху вниз. В каждую клеточку запишем произведение цифр, стоящих над этой клеточкой и справа от неё. При этом цифру десятков произведения напишем над косой чертой, а цифру единиц – под ней.
А теперь будем складывать числа в каждой косой полосе, выполняя эту операцию справа налево. Если сумма окажется меньше 10, то её пишут под нижней цифрой полосы. Если же сумма окажется больше 10, то пишут только цифру единиц суммы, а цифру десятков прибавляют к следующей сумме. В результате получаем нужное произведение: 10063.
Этот способ умножения был очень распространен раньше на Востоке и в Италии. Разбирая его смысл, видим, что в первой косой полосе стоят единицы, во второй – десятки, в третьей – сотни и т.д.
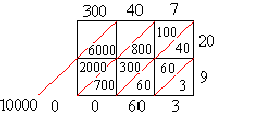
Таким образом, произведение 347 на 29 вычисляется(Таблица 2):
347 · 29 = (300 + 40 + 7) · (20 + 9) = 300 · 20 + (300 · 9 + 40· 20) +
+ (40 · 9 + 7 · 20) +7 · 9 = 6000 + (3000 + 500) + 500 + 63 + (6000 + 3000) + +(500 + 500) + 60 + 3 = 10063.
В « Книге об индийском счете» было впервые дано систематическое изложение арифметики, основанной на индийской десятичной позиционной системе счисления.
Аль-Хорезми первым ввёл в числовой ряд новое число «ноль», что расширило теорию чисел и дало возможность перейти к отрицательным числам. Перевод этого труда на латынь был выполнен в XII веке и хранится сегодня в Кембридже. Арабский текст был утерян.
В латинской транскрипции имя автора — Аль-Хорезми — звучало как «Алгоризми». Поскольку сочинение об арифметике было очень популярно в Европе, это слово стало нарицательным – средневековые европейские математики так называли арифметику, основанную на десятичной позиционной системе счисления. Позднее термин «алгоритм» стал использоваться как общее название любой системы вычислений, выполняемых по строго определённым правилам.
Так имя Мухаммеда Аль-Хорезми перешло в Алгоритми, откуда и появилось слово алгоритм.
«Краткая книга об исчислении ал-джабры и ал-мукабалы»
Около 830 г. Мухаммад ибн Муса Аль-Хорезми составил первый известный арабский трактат по алгебре, заложив, таким образом, основы математической традиции в арабском мире, существовавшей на протяжении столетий.
Алгебраическая работа называется «Китаб ал–джабр ал–мукабала», что означает «Книга о восстановлении и противопоставлении». Это наиболее известная и значительная из всех работ Аль-Хорезми. Общепризнанно, что данный трактат Аль-Хорезми является первым серьезным научным исследованием в данной области знаний.
Причина, по которой он обратился к этой теме, была проста — он планировал учить: «Наиболее легкая и полезная вещь в арифметике, например, то, что постоянно требуется человеку в делах наследования, получения наследства, раздела имущества, судебных разбирательствах, торговых отношениях или при измерении земельных участков, рытье каналов, геометрических вычислениях, а также в других случаях».
Задумывавшаяся как начальное руководство по практической математике, «Краткая книга об исчислении ал-джабры и ал-мукабалы» в первой своей части начинается с рассмотрения уравнений первой и второй степени и далее в двух заключительных разделах переходит к практическому применению алгебры в вопросах мероопределения и наследования.
Книга начинается с введения натуральных чисел, далее идет представление главной темы первого раздела книги — решения уравнений. Все представленные уравнения являются линейными или квадратными и состоят из чисел, их квадратов и корней.
Аль Хорезми показывает, какие числа применяются в алгебре. Если арифметика оперирует с обычными числами, которые “составляются из единиц”, то в алгебре фигурируют числа особого вида – неизвестная величина, ее квадрат и свободный член уравнения.
Неизвестную величину Аль Хорезми называет термином «корень» (джизр) и дает следующее определение:
«Корень – это всякая вещь, умножаемая на себя, будь то число, равное или большее единицы, или дробь, меньшая ее».
Такое определение связано с тем, что при решении уравнений всегда искали не только x, но и x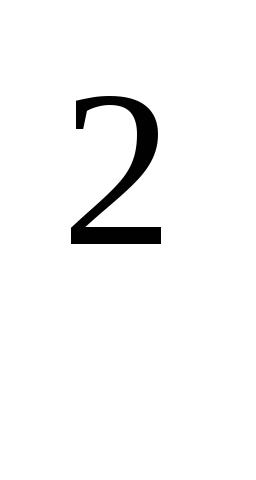
. Поэтому неизвестная рассматривалась как корень из квадрата неизвестной. В определении подчеркивается также, что неизвестная может принимать как целые, так и дробные значения. Термин «корень», применяемый Аль Хорезми, является, по всей вероятности, переводом санскритского слова «Мула» (корень растения), которым обозначали неизвестную в уравнении индийские математики. Позднее в арабской литературе для той же цели применяли термин «вещь» (шай).
Квадрат неизвестной назван словом «имущество» (мал) и определяется как «то, что получается из корня при его умножении на себя». Свободный член уравнения – «простое число» – Аль Хорезми называет «дирхемом»,
т. е. денежной единицей.
Что же означают слова «ал-джабра» и «ал-мукабала»? Ответ на этот вопрос один персидский математик изложил в следующих стихах:
Источник
