Исследовательская работа нестандартные способы нахождения площадей некоторых многоугольников
Введение
Работа посвящена исследованию и сравнению методов измерения площадей фигур произвольной формы.
Актуальность и практическая значимость исследования.
В школьном курсе математики мы в основном имеем дело с многоугольниками. С проблемой вычисления площади фигур я столкнулся при решении различных задач, суть которых сводилась к тому, что требовалось найти площадь различных многоугольников, которых мы не рассматривали на уроках математики. Ведь до 8 класса мы знакомимся только с формулами для вычисления площади квадрата, прямоугольника и прямоугольного треугольника. Так как на уроке мы обычно выполняем решение в тетради, то я обратил внимание, что вычислить площадь того же квадрата помогают клетки, изображенные в тетради. Просматривая различную информацию в интернете, я натолкнулся на формулу, которая позволяет вычислить площадь фигуры, но только не по клеткам, а по их узлам. Между тем, на практике часто возникает необходимость найти площадь фигуры неправильной формы. Например, необходимость определить площадь территории по плану или карте. Но для площадей сложных фигур отсутствуют общие формулы, аналогичные формулам для многоугольников. Впоследствии мне захотелось узнать, есть ли другие способы для вычисления площади различных фигур на клетчатой бумаге, какой из них проще, менее затратен по времени.
Гипотеза: площадь сложной фигуры может быть измерена приближенными методами с точностью, достаточной для практических целей.
Цель работы: исследовать различные способы вычисления площадей фигур, сравнить полученные результаты.
Задачи исследования:
изучить литературу по исследуемой теме;
отобрать интересную и понятную информацию для исследования;
найти различные методы и приёмы вычисления площади фигур на клетчатой бумаге.
изучение методов нахождения площади с помощью взвешивания.
измерение с помощью методов взвешивания площадей контрольных фигур: прямоугольника, квадрата, выявление погрешностей измерения
провести сравнительный анализ «плюсов» и «минусов» найденных способов.
провести эксперимент в 8В классе об выявлении математических знаний у учащихся при вычислении площади фигур;
Поиск интересных задач на нахождение площади фигуры.
проанализировать и систематизировать полученную информацию.
Объектом исследования являются методы измерения площади фигур произвольной формы:
1) метод взвешивания;
2) использование клетчатой бумаги;
3) применение точных формул.
Предметом исследования является площадь фигур произвольной формы.
Из истории возникновения понятия «Площадь».
В повседневной жизни мы часто встречаемся с понятием площади. Мы говорим: площадь квартиры, площадь садового участка и т.д.
Необходимость в понятии «площадь» возникла из жизненных потребностей. В древности люди использовали для измерения длин те измерительные приборы, которые всегда были при себе.
Позже возникла потребность в измерении и сравнении разнообразных «фигур» (н.п. земельных участков). Было необходимо ввести величину, которая характеризовала бы величину той части плоскости, которую занимает фигура. Эту величину назвали площадью.
Измерение площадей является одним из самых древних разделов геометрии. В частности, название “геометрия” означает “землемерие”, т.е. связано именно с измерением площадей. Основы этой науки были заложены в Древнем Египте, где после каждого разлива Нила приходилось заново производить разметку участков, покрытых плодоносным илом, т. е. вычислять их площади.
Вавилоняне, так же как и египтяне измеряли большей частью простейшие фигуры, встречающиеся при межевании земель, возведении стен и насыпей, строительстве плотин и каналов и т.п.
Сохранилось немало планов земельных угодий, разделенных на прямоугольники, трапеции и треугольники, а также планов различных строений, свидетельствующих, что вавилонский землемер или архитектор должен был хорошо чертить и проводить геометрические расчеты.
Многие ученые решали проблему вычисления площади фигуры. В историю с понятием площади вошли имена Евклида, Архимеда, Пифагора, Герона Александрийского, Рене Декарта, Пьера Ферма, Георга Пика и др. Ими открыто большое количество различных формул и способов для вычисления площади фигуры.
Способы вычисления площади фигуры на клетчатой бумаге.
При изучении вычисления площадей многоугольников на клетчатой бумаге я заметил, что все задачи строятся на понятии узла. Узел напоминает узел в рыболовной сетке — пересечение горизонтальных и вертикальных линий. Все задачи достаточно разнообразны и занимательны, они заставляют думать, размышлять, анализировать, искать аналогии.
Рис.1. фотография рыбацкой сетки
Рассмотрим вычисление площади одной и той же фигуры тремя способами и сравним результат вычисления. [1, с.36]
Три способа вычисления площади выпуклого многоугольника.
Разбиение. Смысл данного способа состоит в том, что многоугольник разрезается на прямоугольники и (или) прямоугольные треугольники с вершинами в узлах сетки.
Тогда площадь фигуры можно сосчитать по формуле:
Дополнение до прямоугольника. Смысл данного способа – это дополнение многоугольника до прямоугольника так, чтобы его стороны проходили через вершины четырехугольника, а затем вычитание лишних частей. Получим, что площадь фигуры равна:
Формула Пика. Любая фигура изображенная на листе бумаги делит его на внутреннюю область и внешнюю, а еще есть граничные точки многоугольника. Нас интересуют внутренние узлы и узлы, которые лежат на границе многоугольника. Тогда формула выглядит так S = В + Г/2 — 1, где В — количество внутренних узлов, а Г — количество узлов на границе многоугольника.
Эта формула получила название формула Пика в честь австрийского математика Георга Пика которая появилась в его восьмистраничной работе 1899 года, опубликованной в Праге.
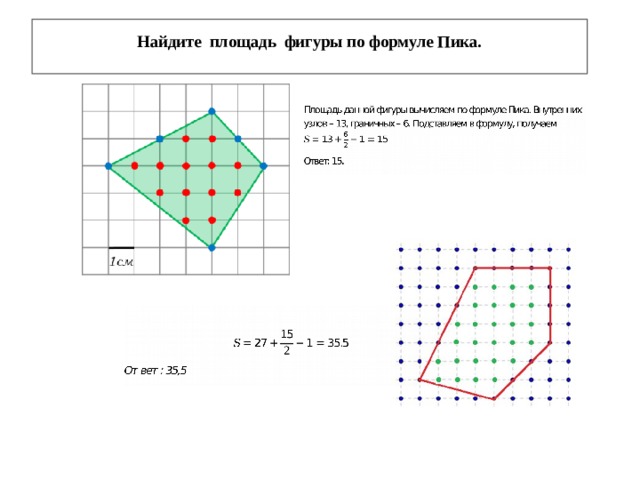
Используя рисунок В= 17, Г = 14, получаем
S = 17 + 14/2 — 1 = 23.
Вычисляя площадь выпуклого многоугольника тремя способами, я получил один и тот же результат.
Три способа вычисления площади невыпуклого многоугольника.
Способ разбиенияне подходит для данной фигуры, т.к. невозможно разбить ее на прямоугольники и (или) прямоугольные треугольники с вершинами в узлах сетки.
Дополнение до прямоугольника.
Достраивая многоугольник до прямоугольника, и отсекая лишние части, найдем площадь фигуры
При подсчете внутренних узлов многоугольника и узлов, лежащих на границе получим, что
В = 5; Г = 4; S = 5 + 4/2 — 1 = 6.
И опять я получил один и тот же результат.
Вычисление площади кольца по формуле Пика.
А если взять не многоугольник, а, например, кольцо и перенести его на клетчатую бумагу? Понятно, что первый и второй способы не удастся использовать. Применим формулу Пика и сравним полученный результат с результатом, полученным используя формулу для вычисления площади круга.
Возьмем кольцо, которое построим с помощью двух окружностей с радиусами R=4 и r = 2.
Вычислим площадь кольца с помощью формулы Пика:
В = 32, Г = 8, S= 32 + 4 — 1 = 35.
Вычислим площадь кольца по формуле площади круга, округлив число π до единиц.
S = πR 2 — πr 2 = 3* 16 — 3*4 = 48 — 12 = 36.
Округлим теперь π до десятых:
S = πR 2 — πr 2 = 3,1* 16 — 3,1*4 = 49,6 — 12,4 = 37,2.
А если округлить число π до сотых, то получим:
S = πR 2 — πr 2 = 3,14* 16 — 3,14*4 = 50, 24 — 12,56 = 37,68.
Сравнив результаты можно сделать вывод, что существует погрешность в вычислении площади по формуле Пика и чем точнее число π, тем она больше. Следовательно, данную формулу можно применять только для вычисления площадей многоугольников. [2, с.17], [4]
Метод взвешивания
Метод измерения вспомогательной величины придуман еще в древности и заключается в измерении массы плоской копии измеряемой фигуры. Если толщина листа, из которого изготовлены взвешиваемая фигура, постоянна, то масса фигуры прямо пропорциональна ее площади. Нужно нанести на плотную бумагу квадрат, площадь которого S0 точно известна, вырезать его и определить на весах его массу m0. На такую же бумагу перенести фигуру с искомой площадью S. Вырезать фигуру и определите её массу m. Затем, пользуясь правилом пропорции – S/S0 = m/m0, вычислить искомую площадь. [3, с.65]
Вычисление площади клинового листа
Для решения задачи была взят фотография кленового листа (рис. 2).
Рисунок 2. Фотография листа клена
Окантовка листа была перенесена на лист бумаги и была разбита (разрезана) на прямоугольники и (или) прямоугольные треугольники. (Рисунок 3).
Рисунок 3. Разбиение листа клена на прямоугольники и прямоугольные треугольники
После чего произведен расчет площади каждого прямоугольника и прямоугольного треугольника в см 2
Тогда общая площадь листа будет равна:
см 2
2. Дополнение до прямоугольника.
Окантовка листа была перенесена на лист бумаги и была дополнена до прямоугольника. (Рисунок 4).
Рисунок 4. Дополнение листа клена на прямоугольника
После чего произведен расчет площади общего прямоугольника и каждого прямоугольника и прямоугольного треугольника в см 2
Общий прямоугольник имеет размеры 18,2 см на 15 см, т. Е. его площадь прямоугольника составляет S=18,2∙15=273 см 2
см 2
Окантовка листа была перенесена на миллиметровую бумагу. (Рисунок 5).
Рисунок 5. Разбиение листа клена на узлы
В (внутренние точки) =13353 шт.
Г (граничные точки) = 725 шт.
Тогда по формуле S = В + Г/2 – 1
S=13353+362,5-1=13714,5мм 2 =137,145 см 2
4. Метод взвешивания
Для проведения взвешивания взяли лист бумаги SvetoCopy. По ее плотности определили вес бумаги при помощи таблицы и путем взвешивания. Результаты сошлись. Вес одного листа бумаги А4 =5г. Размеры листа А4 равны 210х297мм, т.е. площадь одного листа равна S0 = 623,7 см 2
Рис. 6. Фотография оборотной стороны упаковки бумаги SvetoCopy
Рис. 7. Таблицы дляболее точного измерения массы листа по его плотности.
Для определения погрешности вычислений вырезали в качестве эталонов несколько геометрических фигур (прямоугольник (эталон 1) и квадрат (эталон 2)), площадь которых можно сравнить вычислив ее по формуле.
Прямоугольник имеет размеры: 7см на 5 см, а квадрат: 5см на 5см.
Источник
Нестандартные способы нахождения площадей могоугольников. Формула Пика.
При подготовке к экзамену по математике в 9 к лассе есть задачи на нахождение площади многоугольника. Кроме основных способов нахождения площади по формуле, можно использовать формулу Пика. Данная формула позволяет решить задачу быстро, если многоугольник показан на клетчатой бумаге.
Содержимое разработки
Нестандартные способы нахождения площадей многоугольников. Формула Пика.
Подготовила учитель математики высшей категории МОУ Новоульяновская СШ № 2 Пивоварова В.Н.
Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать.
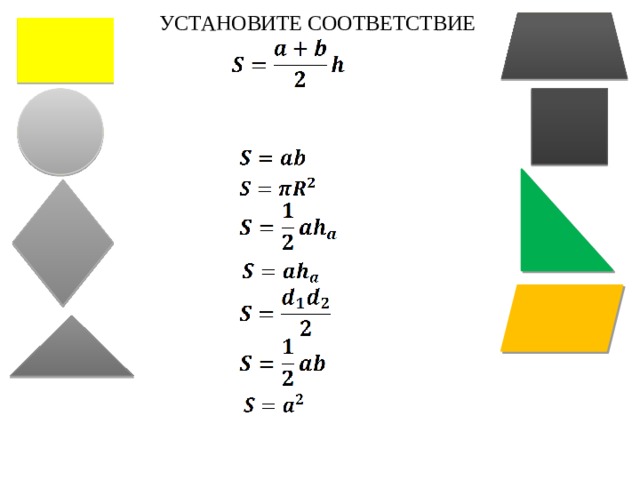
Давайте повторим основные формулы нахождения площадей, которые нам пригодятся сегодня на уроке.
Необходимо нажать на формулу маркером от интерактивной доски для проверки.
Методы нахождения площади многоугольника.
- Метод непосредственного применения формул.
- Метод сложения площадей
- Метод вычитания площадей простых фигур из площади прямоугольника, построенного вокруг данной фигуры
- Формула Пика
Георг Александр Пик,
Формула была открыта в 1899 г.
Площадь искомой фигуры можно найти по формуле:
В — количество целочисленных точек внутри многоугольника
Г — количество целочисленных точек на границе многоугольника
Найдите площадь фигуры по формуле Пика.
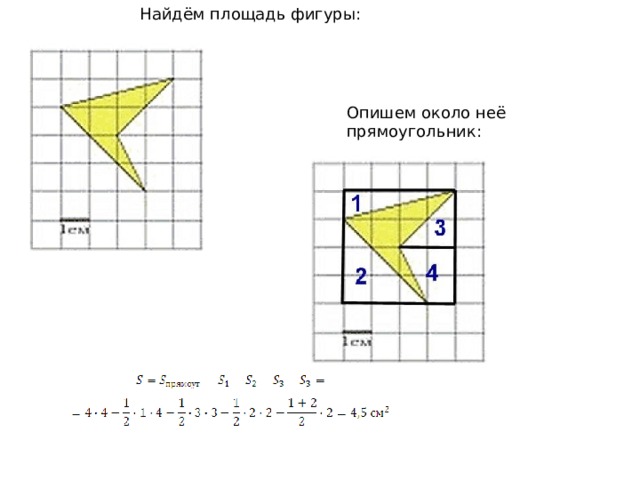
Найдём площадь фигуры:
Опишем около неё прямоугольник:
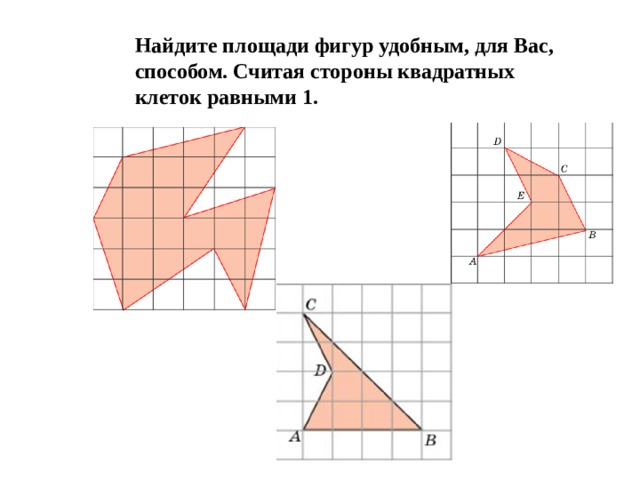
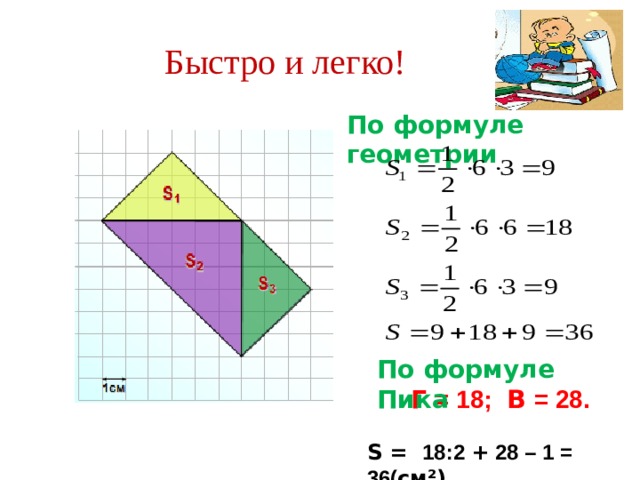
Найдите площади фигур удобным, для Вас, способом. Считая стороны квадратных клеток равными 1.
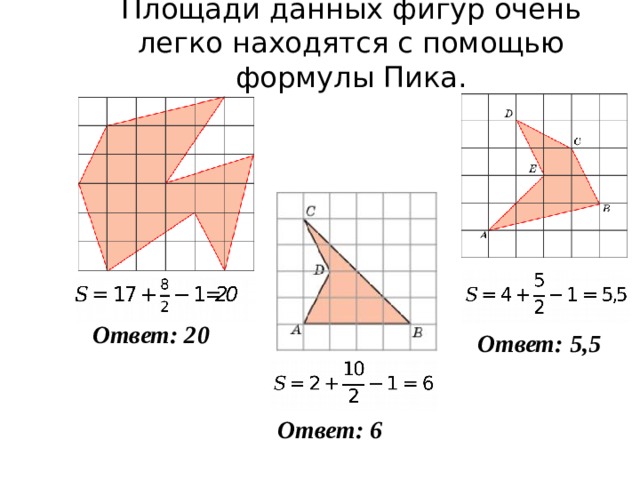
Площади данных фигур очень легко находятся с помощью формулы Пика.
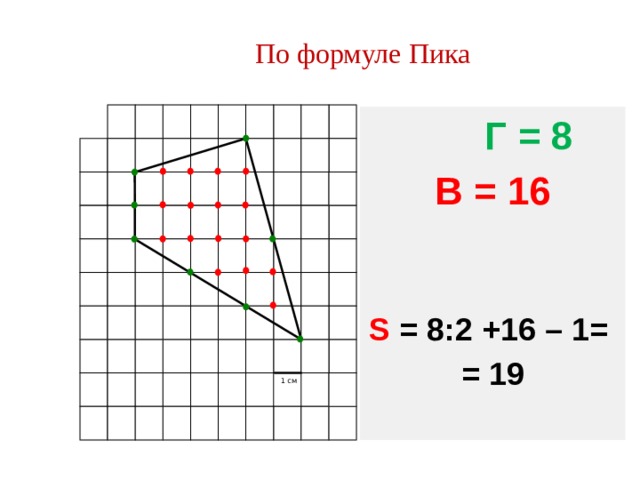
По формуле Пика
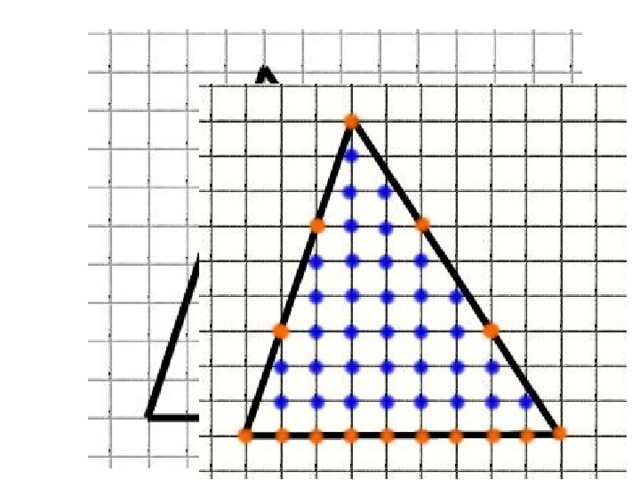
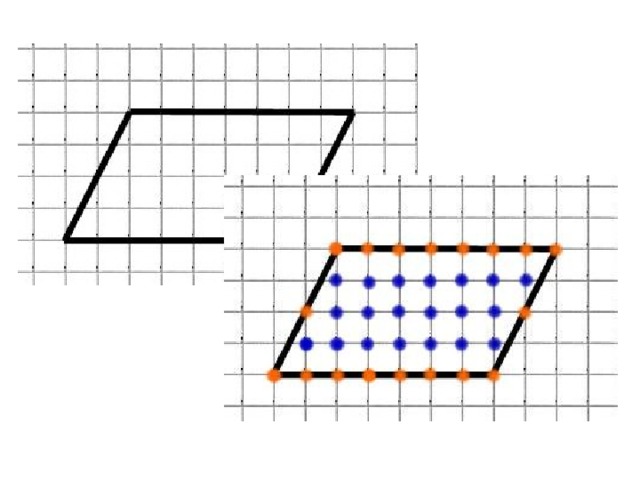
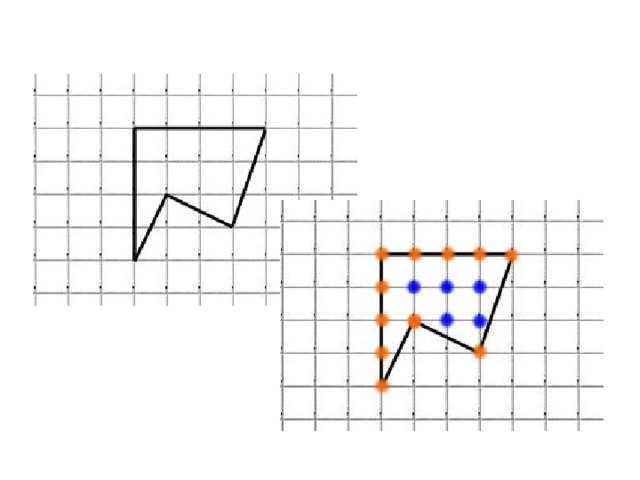
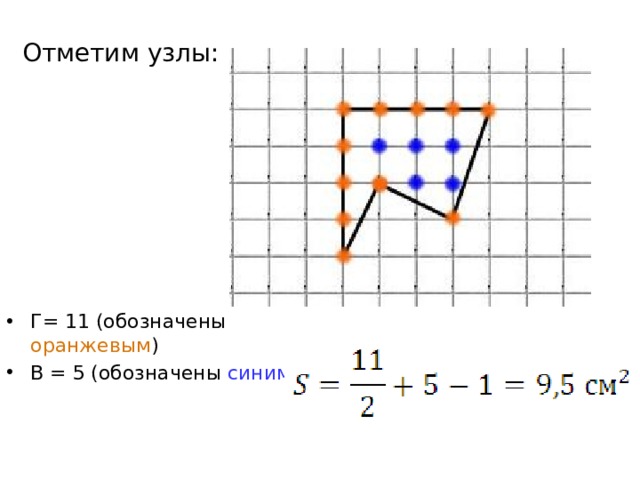
- Г= 11 (обозначены оранжевым )
- В = 5 (обозначены синим )
Источник