Исследование функций элементарными способами

Содержание

Элементарное исследование функции
Алгебра и начала математического анализа. 11 класс
Исследование функций и построение их графиков элементарными методами
Просмотр содержимого документа «Исследование функций и построение их графиков элементарными методами»

Элементарное исследование функции

Исследовать функцию – значит охарактеризовать ее поведение при изменении независимой переменной. Для элементарного исследования необходимо:

· найти область определения функции;

· определить нули функции, точки пересечения графика с осями координат;

· исследовать на четность/нечетность;

· исследовать на периодичность.

Область определения – это множество всех значений аргументов функции, при которых она имеет смысл.

Нули функции – это те значения ее аргумента, при которых функция равна нулю.

Функция называется четной, если она задана на симметричном относительно начала координат промежутке и если f(-x) = f(x), и нечетной если f(-x) =-f(x). Для того чтобы установить четность или нечетность функции, требуется определить, является ли область определения функции интервалом, симметричным относительно начала координат, и выполняется ли одно из условий: f(-x) = f(x) или f(-x) = -f(x). Если функция не является четной и не является нечетной, то она называется функцией общего вида. График четной функции симметричен относительно оси ординат. График нечетной функции симметричен относительно начала координат.

Функция называется периодической с периодом Т, если f(x) = f(x + Тп), n 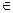Z.

Источник

Алгебра и начала математического анализа. 11 класс

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №48. Функции. Свойства функций и их графики. Исследование функций.

Перечень вопросов, рассматриваемых в теме:

функция, аргумент функции, значение функции
график функции, преобразование графика функции
свойства функции, исследование свойств функции

Глоссарий по теме урока

Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у.

х – независимая переменная, аргумент,

у — зависимая переменная, значение функции

Множество значений аргумента функции называется областью определения функции и обозначается D(y).

Множество значений, которые принимает сама функция, называется множеством значений функции и обозначается Е(у).

Функция у = f(х) называется четной, если она обладает двумя свойствами:

область определения этой функции симметрична относительно 0;
для любого х из области определения выполняется равенство f(-х)=f(х).

Функция у = f(х) называется нечетной, если она обладает двумя свойствами:

область определения этой функции симметрична относительно 0;

для любого х из области определения выполняется равенство f(-х)=-f(х).

Значения аргумента, при которых значение функции равно 0, называются корнями (нулями) функции.

Функция у=f(x) возрастает на промежутке (а; в), если для любых х₁, х₂ из этого промежутка, таких, что х₁ у₂.

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл.– М.: Просвещение, 2015. С. 98-118, 271-307.

Шахмейстер А.Х. Построение и преобразование графиков. Параметры. Ч.2-3. СПб.: Петроглиф; М.: МЦНМО, 2016. 392 с. С.73-307.

Открытые электронные ресурсы:

Образовательный портал “Решу ЕГЭ”.

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.

Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.

Теоретический материал для самостоятельного изучения

1. Исследование функции и построение графика

Схема исследования функции на примере функции

1) Область определения функции

Знаменатель дроби не равен нулю:

Получили область определения

D(y)=

Множество значений функции

Отыскание Е(у) можно свести к решению уравнения с параметром у. Все значения параметра у, при которых уравнение имеет хотя бы одно решение, и составят Е (у).

Получили

Четность / нечетность функции

D(y)= — симметрична относительно нуля

следовательно, функция четная и ее график симметричен относительно оси ОУ

Для нахождения нулей функции необходимо решить уравнение

Уравнение не имеет действительных корней, значит, нулей у данной функции нет, ее график не пересекает ось ОХ

у>0 при

у 2 у.е. Если на втором объекте работает t человек, то их суточная зарплата составляет t 2 у.е. Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у.е. в этом случае придется заплатить рабочим?

1 этап. Ведем переменную, выразим нужные компоненты, составим искомую функцию.

Пусть на 1 объект направлено х рабочих, суточная зарплата которых составит 4x 2 у.е.

Тогда на 2 объект направлено (24 — x) рабочих – суточная заработная плата (24 — x) 2 (у.е.)

Всем рабочим нужно заплатить 4x 2 +(24 — x) 2 = 5x 2 -48x+576 (у.е.)

Причем 0≤ x ≤ 24, x ϵ N.

Рассмотрим функцию f(x)=5x 2 -48x+576.

Функция квадратичная, старший коэффициент положителен, следовательно, наименьшее значение в вершине при x₀ = 4,8 .

3 этап. Перевод на язык задачи

Поскольку x ϵ N, подходящим будет ближайшее к вершине натуральное значение, x=5 (рабочих) – на 1 объекте.

24-5=19 (рабочих) – на 2 объекте.

Наименьшее значение f(5)=125+240-576=461 (у.е.) – наименьшая суточная выплата.

Примечание: исследовать функцию также можно было с помощью производной.

Ответ: 5 рабочих на 1 объекте, 19 – на втором, 461 у.е. – наименьшая суточная выплата.

Примеры и разбор решения заданий тренировочного модуля

1. Исследуйте функции на четность.

область определения – множество действительных чисел – симметрична относительно нуля

у(-х)=0, что можно интерпретировать и как у(х), и как –у(х). К тому же график этой функции – прямая, совпадающая с осью ОХ, — симметричен относительно оси ОУ и относительно начала координат.

Данная функция одновременно четна и нечетна.

область определения – множество действительных чисел – симметрична относительно нуля

преобразуем функцию, применив формулы приведения: sin(x+5π/2)=cos x

у= cos x – четная функция, значит, исходная функция также четная

логарифмируемое выражение должно быть положительным

Область определения несимметрична относительно 0, значит, в проверке второго условия нет необходимости, — функция общего вида.

Найдем область определения D(f)

Проверим второе условие

Полученное в результате подстановки –х в функцию выражение, очевидно, не равно f(x), не дает пока понимания о выполнении условия нечетности.

Зайдем с другого конца, выразим -f(x):

домножим на сопряженное

Теперь можем сделать вывод: f(-x)=-f(x), функция нечётная.

и четная, и нечетная

Используем функциональный подход при решении данной задачи. Представим каждое из уравнений как функции. Построим их графики. Единственное решение системы будем интерпретировать как единственную точку пересечения графиков функций первого и второго уравнений.

Второе уравнение проще, но содержит параметр. Перепишем его в явном виде для функции, выразив у: у=-х+а.

В таком виде понятно, что данное уравнение задает множество прямых, параллельных у=-х.

Источник

Исследование функций и построение их графиков элементарными методами

Просмотр содержимого документа
«Исследование функций и построение их графиков элементарными методами»

Исследование функций элементарными методами и построение их графиков.

Содержательные: выявление уровня знаний обучающихся, систематизации знаний, формулирование обобщения знаний по теме урока
Деятельностные : создание условий для самооценки обучающихся, развитие пространственного мышления, творческих способностей, навыков самостоятельной работы, умения работать в группе, развитие познавательного интереса, обучение приемам самоанализа, сопоставления, сравнения, развитие умения обобщения, систематизации знаний.

Постройте эскиз графика функции по данному исследованию (работа в парах).

Область определения функции y = (x). Обозначение: D(f) или D(y)

функция задана формулой

Множество значений Функции y = (x). Обозначение: E( )или E(y)

Чётность функции, нечётность функции y = (x)

Периодичность функцииy = (x)

Нули функции y = (x)

Промежутки знакопостоянства функции y = (x)

Промежутки монотонности (возрастания, убывания) функции y = (x)

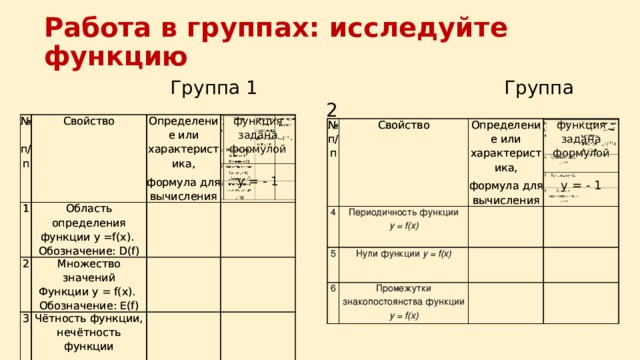
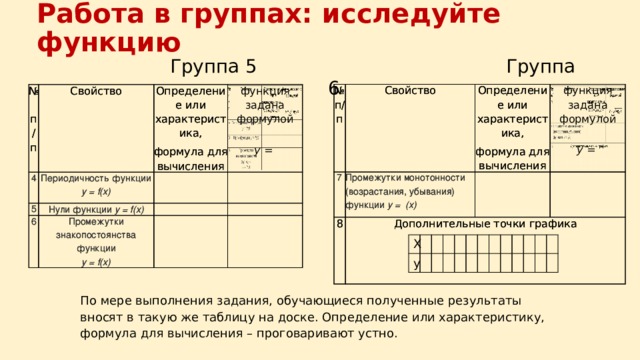
Работа в группах: исследуйте функцию

Область определения функции y =f(x). Обозначение: D(f)

Определение или характеристика,

Множество значений Функции y = f(x). Обозначение: E(f)

формула для вычисления

Множество значений Функции y = f(x). Обозначение: E(f)

формула для вычисления

функция задана формулой

Чётность функции, нечётность функции

Определение или характеристика,

формула для вычисления

Нули функции y = f(x)

функция задана формулой

формула для вычисления

Нули функции y = f(x)

Промежутки знакопостоянства функции y = f(x)

Работа в группах: исследуйте функцию

Область определения функции y =f(x). Обозначение: D(f)

Промежутки монотонности (возрастания, убывания) функции y = (x)

Область определения функции y =f(x). Обозначение: D(f)

Промежутки монотонности (возрастания, убывания) функции y = (x)

Определение или характеристика,

Множество значений Функции y = f(x). Обозначение: E(f)

формула для вычисления

Множество значений Функции y = f(x). Обозначение: E(f)

функция задана формулой

формула для вычисления

Дополнительные точки графика

функция задана формулой

формула для вычисления

Чётность функции, нечётность функции

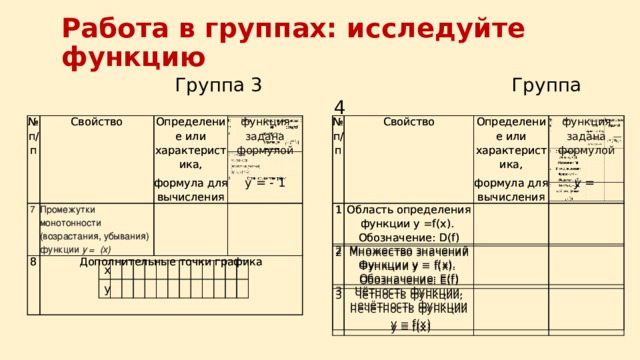
Работа в группах: исследуйте функцию

Промежутки монотонности (возрастания, убывания) функции y = (x)

Определение или характеристика,

функция задана формулой

формула для вычисления

Дополнительные точки графика

Определение или характеристика,

формула для вычисления

функция задана формулой

Нули функции y = f(x)

формула для вычисления

Нули функции y = f(x)

Промежутки знакопостоянства функции y = f(x)

По мере выполнения задания, обучающиеся полученные результаты вносят в такую же таблицу на доске. Определение или характеристику, формула для вычисления – проговаривают устно.

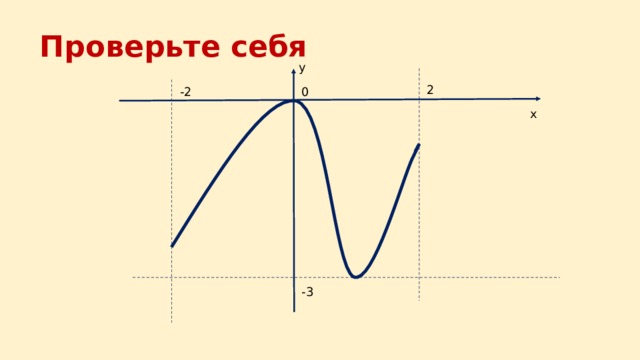
Постройте графики функций по Вашим исследованиям

На маркерной доске:

График функции y = — 1 строит обучающийся из 4-6 группы

График функции y = строит обучающийся из 1-3 группы

Обучающиеся класса строят два графика в тетрадях, затем проверяют работу друг друга, оценивают ее. Обучающийся сравнивает свою оценку с оценкой товарища и выставляет средний балл.

Каким еще способом можно построить

один из графиков данных функций?

ВЫВОД: График функции y = — 1 можно построить и движением графика функции y = вдоль оси абсцисс на 3 единицы влево и вдоль оси ординат на 1 единицу вниз. (строим движением эскиз графика функции y = — 1 и сравниваем с построенным ранее графиком функции на маркерной доске)

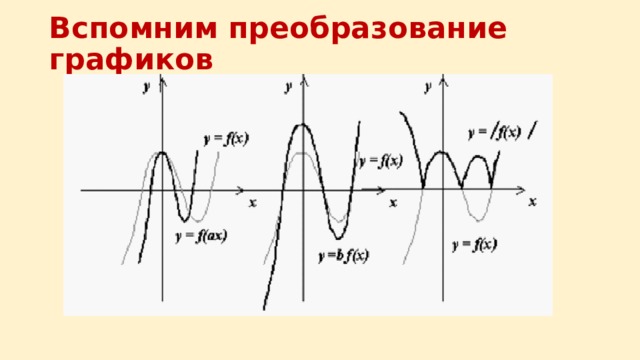
Вспомним преобразование графиков

Итог –синквейн Синквейн — это анализ и синтез информации, игра слова.

Тема урока – одним словом.
Ответьте, используя прилагательные, какая функция?
Опишите действия, используя глаголы, что мы делаем с ней?
Составьте предложение или словосочетание, которое выражает Ваше отношение к теме, и является своеобразным выводом.
Подведите итог, выразив его одним словом.

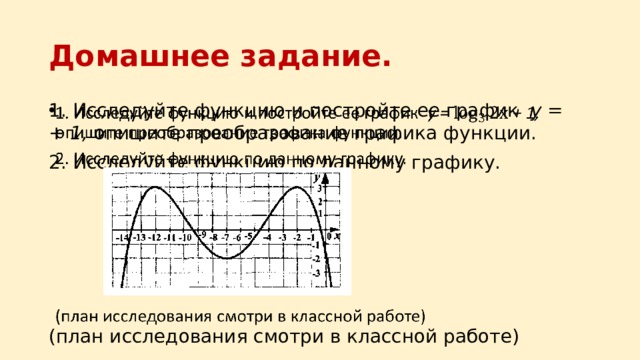
1. Исследуйте функцию и постройте ее график y = + 1, опишите преобразование графика функции.

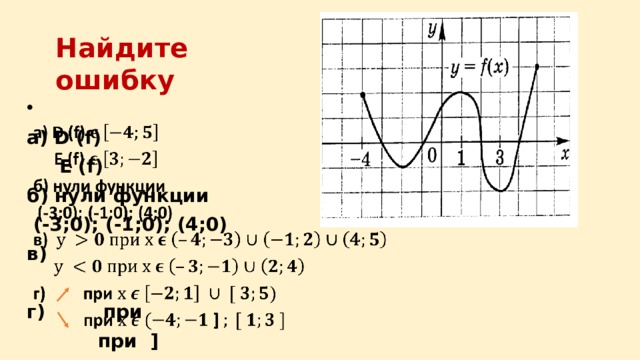
2. Исследуйте функцию по данному графику.

(план исследования смотри в классной работе)

Источник

Исследование функций элементарными способами

Элементарное исследование функции

Алгебра и начала математического анализа. 11 класс

Конспект урока

Исследование функций и построение их графиков элементарными методами

Просмотр содержимого документа «Исследование функций и построение их графиков элементарными методами»

Просмотр содержимого документа
«Исследование функций и построение их графиков элементарными методами»