Используя способ задания новой плоскости проекций найти расстояние от точки е до плоскости

Метод замены плоскостей проекций

Для решения целого ряда задач начертательной геометрии наиболее рациональным является метод замены плоскостей проекций. Например, с его помощью можно определить натуральную величину плоской фигуры, расстояние между параллельными прямыми, опорные точки пересечения поверхностей.

Замена одной плоскости проекции

Сущность метода заключается в замене одной из плоскостей проекций на дополнительную плоскость, выбранную так, чтобы в новой системе плоскостей решение поставленной задачи значительно упрощалось. Положение фигур в пространстве при этом не меняется.

Рассмотрим на примере точек A и B, как осуществляются построения на комплексном чертеже. Изначально точка A находится в системе плоскостей П₁, П₂. Введем дополнительную горизонтальную пл. П₄. Она будет перпендикулярна фронтальной плоскости проекций П₂ и пересечет её по оси x₁. Эту ось необходимо провести на комплексном чертеже с учётом цели построения. Здесь мы расположили её произвольно.

В новой системе плоскостей положение точки A» не изменится. Чтобы найти точку A’₁, которая является проекцией т. А на плоскость П₄, проведем из A» перпендикуляр к оси x₁. На этом перпендикуляре от точки его пересечения с осью x₁ отложим отрезок A_x1А’₁, равный отрезку A_xA’.

Данные построения основаны на равенстве ординат точек A’ и А’₁. Действительно, в системе плоскостей П₁, П₂ и в системе П₂, П₄ точка A удалена от фронтальной плоскости проекций П₂ на одно и то же расстояние.

Теперь осуществим перевод точки B в новую систему плоскостей П₁, П₄ (рис. ниже). Для этого введем произвольную фронтальную пл. П₄, которая будет перпендикулярна горизонтальной плоскости проекций П₁ и пересечет её по оси x₁.

В системе П₁, П₄ положение точки B’ останется неизменным. Чтобы найти точку B»₁, проведем из B’ перпендикуляр к оси x₁. На этом перпендикуляре от точки его пересечения с осью x₁ отложим отрезок B_x1B»₁ равный отрезку B_xB». Описанные построения основаны на равенстве аппликат точек B» и B»₁.

Замена двух плоскостей проекций

Иногда для решения поставленной задачи требуется замена двух плоскостей проекций (рис. ниже). Пусть A’ и A» – исходные проекции точки A, находящейся в системе пл. П₁, П₂. Введем первую дополнительную плоскость П₄ и определим новую горизонтальную проекцию A’₁ точки A, как это было описано ранее.

Для осуществления второй замены плоскости проекций будем рассматривать систему пл. П₂, П₄ в качестве исходной. Введем новую фронтальную плоскость П₅ перпендикулярно горизонтальной пл. П₄. Для этого на произвольном месте чертежа проведем ось x₂ = П₄ ∩ П₅. Из точки A’₁, положение которой останется неизменным, восстановим перпендикуляр к оси x₂. На нем от точки A_x2 отложим отрезок A_x2A»₁ равный отрезку A»A_x1.

Использование метода замены при решении задач

Владея методом замены применительно к одной точке, можно построить дополнительные проекции любых фигур, поскольку они представляют собой множество точек. На рисунке ниже показан перевод отрезка AB в частное положение. Новая плоскость П₄ проведена параллельно AB, поэтому отрезок проецируется на неё в натуральную величину.

На следующем рисунке показана плоскость общего положения α, заданная следами. Переведем её в новую систему плоскостей П₁, П₄ так, чтобы α занимала проецирующее положение. Для этого перпендикулярно горизонтальному следу h_0α введем дополнительную фронтальную плоскость П₄.

Новый фронтальный след f_0α1 строится по двум точкам. Одна из них, X_α1, лежит на пересечении h_0α с осью x₁. Дополнительно возьмем точку N, принадлежащую α, и укажем её фронтальную проекцию N»₁ на плоскости П₄.

Определение расстояния между параллельными плоскостями

Параллельные плоскости α и β расположены так, как показано на рисунке. Чтобы найти расстояние между ними, необходимо из произвольной точки A, взятой на пл. α, опустить перпендикуляр AB на пл. β и определить его настоящую длину.

Для уменьшения количества геометрических построений α и β предварительно переводятся в проецирующее положение с помощью метода замены плоскостей проекций. Вспомогательная точка M используется для определения направления следов f_0β1 и f_0α1, параллельных друг другу.

Источник

Определение расстояния от точки до плоскости

Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из точки на плоскость, и в начертательной геометрии определяется графически согласно следующему алгоритму.

1. Плоскость переводят в проецирующее положение с помощью методов преобразования ортогональных проекций.
2. Из точки на плоскость опускают перпендикуляр и находят его длину. Направление проекции перпендикуляра определяется на основании теоремы о проецировании прямого угла.

Рассмотрим, как реализуется составленный нами алгоритм на практике. На рисунке ниже представлены графические построения, необходимые для определения расстояния между точкой N и плоскостью α, заданной треугольником ABC.

• Через вершину B» треугольника A»B»C» проводим проекцию h» горизонтали h. По линиям связи находим h’.
• Переводим ABC в проецирующее положение. Для этого перпендикулярно h вводим новую фронтальную плоскость П₄. Проецируем на неё точку N и треугольник ABC.
• Из точки N»₁ проводим N»₁M»₁ ⊥ A»₁C»₁. Длина отрезка N»₁M»₁ – искомое расстояние между плоскостью треугольника ABC и точкой N.

Требуется определить величину расстояния между точкой K и плоскостью β, заданной следами. В отличие от предыдущей задачи здесь нет необходимости проводить линию уровня, так как её роль выполняет проекция h_0β.

• Переводим плоскость β в проецирующее положение. Для этого перпендикулярно следу h_0β вводим дополнительную фронтальную плоскость П₄. На прямой f_0β берем произвольную точку E, определяем её проекции E», E’ и E»₁. Через E»₁ и X_0α1 проводим прямую f_0β1, которая является следом плоскости β на П₄. По линии связи определяем проекцию K»₁ точки K.
• Из K»₁ проводим перпендикуляр K»₁M»₁ в направлении прямой f_0β1. Длина отрезка K»₁M»₁ – величина искомого расстояния от K до β.

Если требуется перевести отрезок KM в исходную систему плоскостей, то это делается с помощью обратных преобразований, как показано на следующем рисунке.

Источник

Расстояние от точки до плоскости

Определить: Расстояние от точки до плоскости.

Дано: Четырехугольник EBCD и точка A.

Таблица значения координат.

Вариант	Значения координат
	XA	YA	ZA	XB	YB	ZB	XC	YC	ZC	XD	YD	ZD	XE	YE	ZE
1	90	105	50	60	90	80	10	60	80	40	30	10	90	60	10

Мы уже определяли расстояние от точки до плоскости только способом прямоугольного треугольника. В этом видеоуроке также определим расстояние от точки до плоскости только способом замены плоскостей проекций.

• Преобразуем плоскость общего положения четырехугольника EBCD в плоскость фронтально-проецирующую.
  • Строим новую ось проекций X14 перпендикулярно горизонтали плоскости четырехугольника EBCD.
  • Координату Z для плоскости П1 снимаем с плоскости П2.

Перпендикуляр А4К4 и есть расстояние от точки до плоскости, т.к. он проецируется в отрезок натуральной величины.

С помощью линий связи строим перпендикуляр к плоскости четырехугольника EBCD. На плоскость П1 координату Z берем с плоскости П4.

Более подробно в видеоуроке по начертательной геометрии в Автокад

Источник

Определить расстояние от точки D до плоскости треугольника АВС (пример выполнения)

РЕШЕНИЕ: Расстояние от точки до плоскости определяется длиной отрезка перпендикуляра, проведенного из заданной точки к заданной плоскости.

Далее приводится поэтапное графическое решение варианта №17 из данного списка вариантов.

Задачу решаем в следующей последовательности:

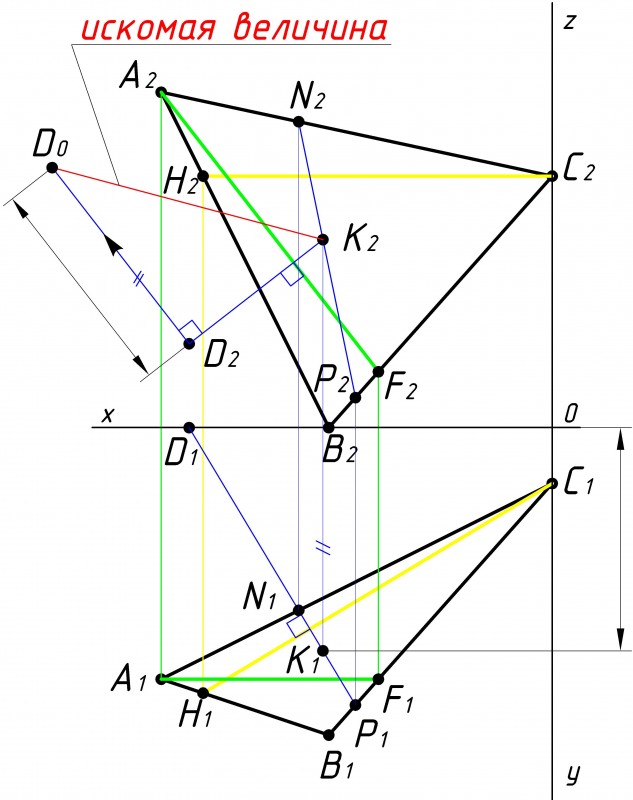
Рис.1

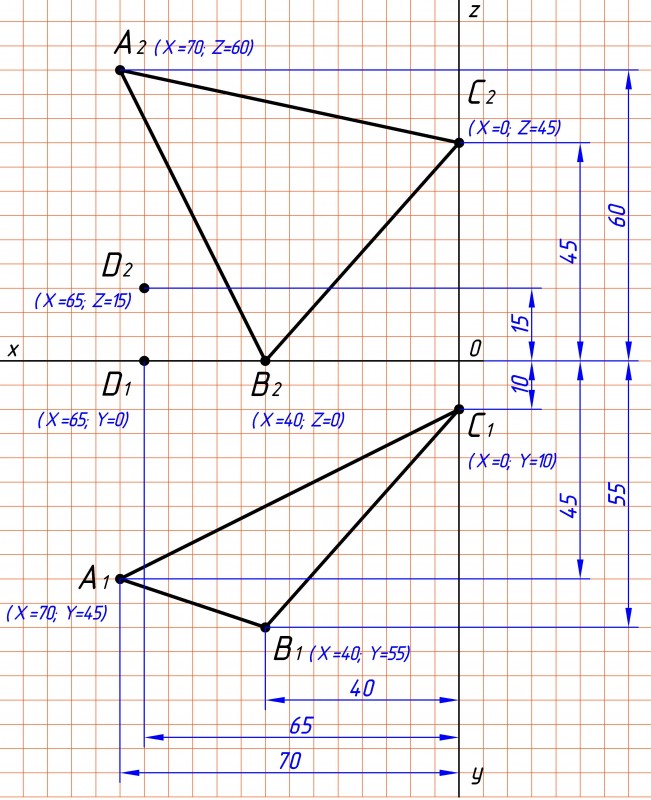
Строим плоскость треугольника АВС и точку D по заданным координатам варианта №17 (см. рис.1):

A (70, 45, 60),
B (40, 55, 0),
C (0, 10, 45),
D (65, 0, 15).

Построить свой треугольник онлайн можно перейдя по ссылке.

Рис.2

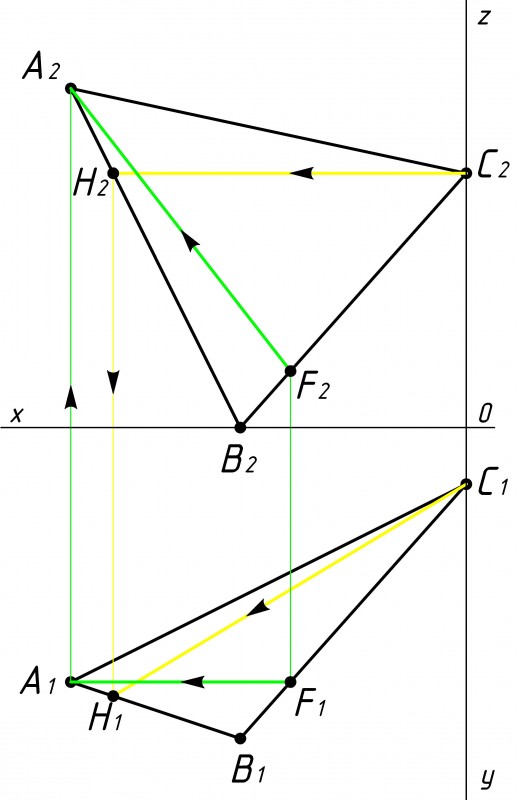
Затем строим в плоскости треугольника АВС фронталь и горизонталь (см. рис.2).

Фронталь это линия, которая параллельна оси ОХ на горизонтальной плоскости проекции (нижняя часть).
А горизонталь — линия, которая параллельна оси ОХ на фронтальной плоскости проекции (верхняя часть).

Данные линии проводятся через вершины треугольника (через точки А, B, C). В нашем случае через вершину А мы проводим фронталь AF, а через вершину С проводим горизонталь CH.

Рис.3

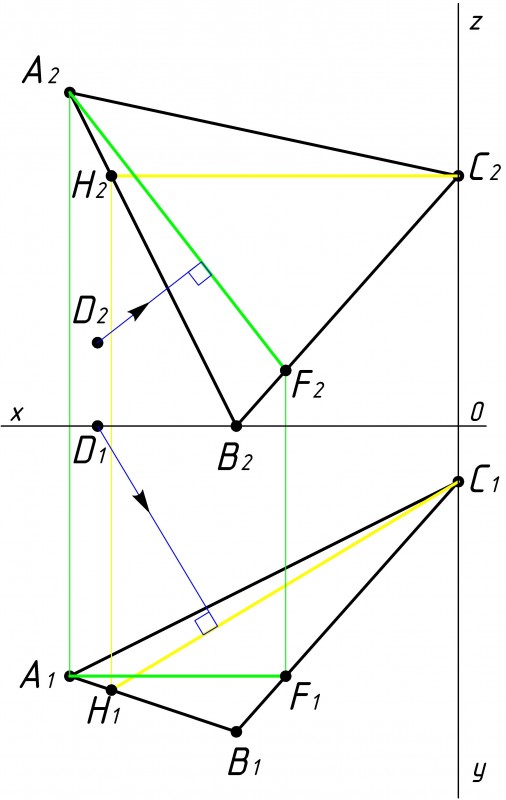
После того как мы построили фронталь и горизонталь, необходимо из точки D провести перпендикуляр к треугольнику АВС(см. рис.3).

При этом горизонтальная проекция перпендикуляра (от точки D₁) должна быть перпендикулярна к горизонтальной проекции горизонтали C₁H₁.

А фронтальная проекция (от точки D₂) перпендикулярна к фронтальной проекции фронтали A₂F₂;

Рис.4

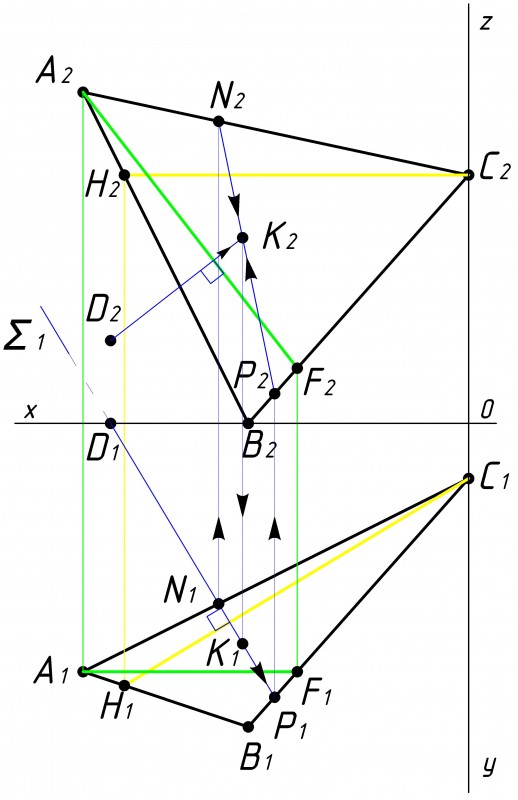
Теперь необходимо определить точку пересечения перпендикуляра с данной плоскостью, заключив перпендикуляр во вспомогательную плоскость частного положения (см. рис.4).

Перпендикуляр через точку D₁ заключаем во вспомогательную плоскость частного положения ∑₁

Примечание: необязательно это делать через точку D₁, результат через точку D₂ будет идентичным.

Так же необязательно рисовать вспомогательную плоскость частного положения ∑₁, ее можно просто представить, что мы ее там проводим.

После того как мы провели вспомогательную плоскость ∑₁ находим точки пересечения данной плоскости (M₁P₁) с треугольником АВС. Проецируем их на фронтальную плоскость проекции и получаем точки M₂P₂.

Потом находим точку пересечения линии M₂P₂ вспомогательной плоскости с перпендикуляром от точки D₂ и отмечаем точку К₂. Проецируем точку К₂ на горизонтальной плоскости проекции и получаем точку К₁.

Рис.5

После того как мы провели перпендикуляр DK, осталось определить его действительную величину способом прямоугольного треугольника (см. рис.5).

Определяем расстояние по вертикали от точки D до точки K на какой-либо плоскости проекций. Например на горизонтальной (нижней) плоскости проекции.

Примечание: доказательство того что расстояние от точки до плоскости можно определить на любой из плоскостей приекции представлено здесь.

Откладываем это расстояние перпендикулярно отрезку DK на противоположной плоскости проекции (в нашем случа на фронтальной) от любой из вершин (например от точки D) и получили нулевую точку D₀.

Расстояние от точки D₀ до точки K₂ и является искомым расстоянием от точки D до плоскости треугольника АВС.

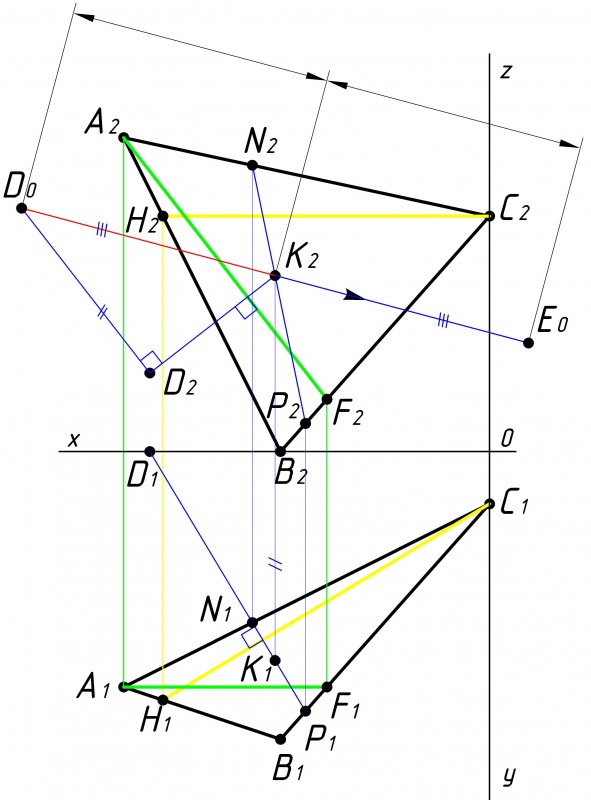
Рис.6

Найдя расстояние от точки до плоскости треугольника АВС, можно начать строить точку симметричную точке D относительно данного треугольника (см. рис.6).

Симметричная точка подразумевает собой точку, которая отстоит от плоскости треугольника АВС на таком же расстоянии, что и точка D, но с противоположной стороны.

Рассмотрим полученный нами отрезок D₀K₂. В противоположную сторону от точки K₂ откладываем отрезок равный D₀K₂. Ставим точку Е₀.

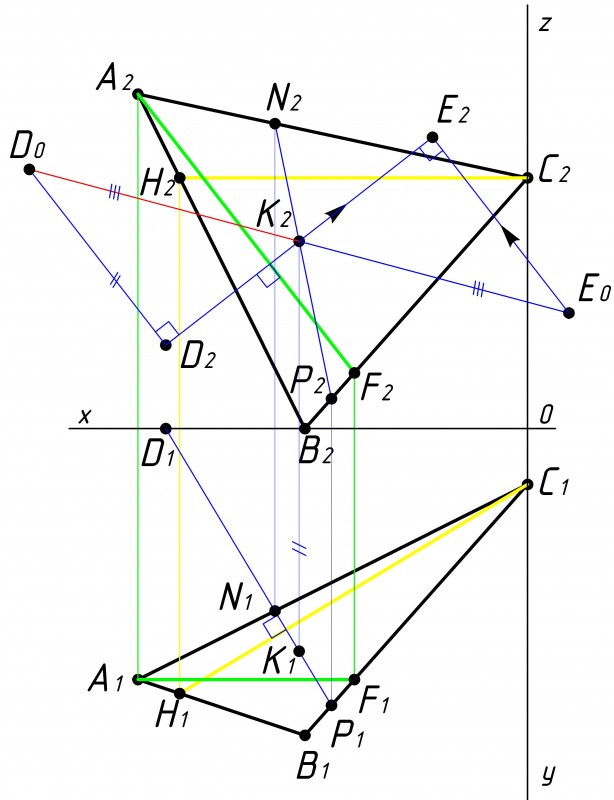
Рис.7

Затем проводим перпендикуляр к линии пенпендикуляра от точки D на рассматриваемой плоскости проекции (см. рис.7).

В нашем случае на фронтальной плоскости проекции к удлиненной линии D₂K₂. На пересечении ставим точку Е₂.
Линии D₂K₂ и К₂Е₂ так же равны между собой.

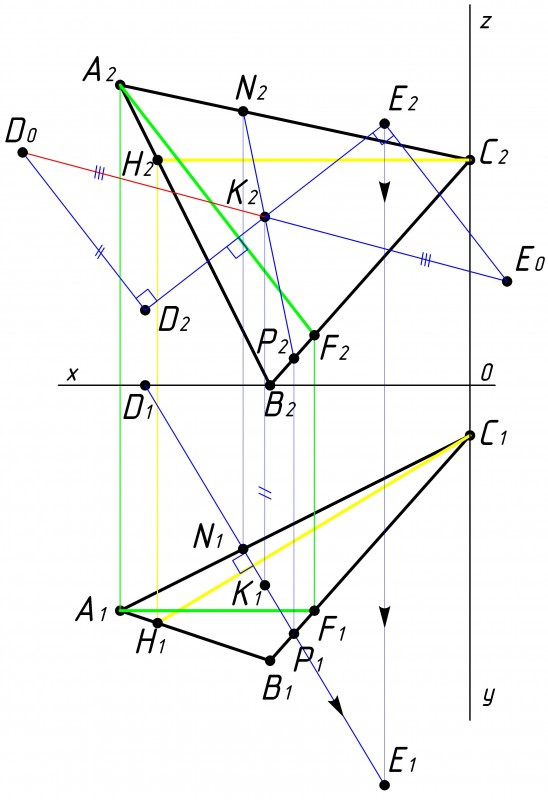
Рис.8

Строим проекцию полученной точки на противоположную плоскость проекции так же на линию перепендикуляра (см. рис.8).

Источник