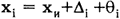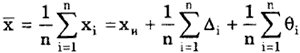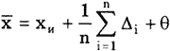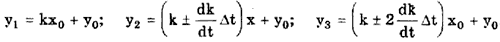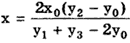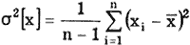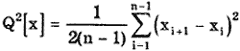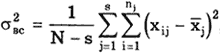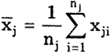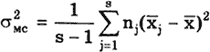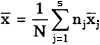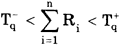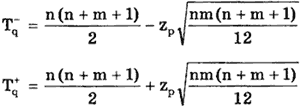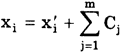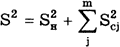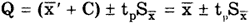Используя способ последовательных разностей определить присутствует ли систематическая погрешность

Пример 3.1

Используя способ последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений, приведенных во втором столбце таблицы 3.2.

Результаты наблюдений

n	xi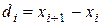
13,4	-0,1	0,01	-0,6
13,3	+1,2	1,44	-0,7	0,49
14,5	-0,7	0,49	+0,5	0,25
13,8	+0,7	0,49	-0,2	0,04
14,5	+0,1	0,01	+0,5	0,25
14,6	-0,5	0,26	+0,6	0,86
14,1	+0,2	0,04	+0,1	0,01
14,3	+0,3	0,09	+0,3	0,09
14,0	+0,3	0,09	0,0	0,0
14,3	-1,1	1,21	+0,3	0,09
13,2	—	—	-0,8	0,64
Σ 154,0	-0,2	4,12	0,0	2,58

Для приведенного ряда результатов вычисляем:

среднее арифметическое =154,0/11=14;

оценку дисперсии S 2 [х]=2,58/10=0,258;

значение Q 2 [х]=4,12/(2·10)=0,206;

критерий Аббе ν=0,206/0,258=0,8.

Как видно из таблицы 3.1, для всех уровней значимости (q=0,001; 0,01 и 0,05) при n=11 имеем ν>ν_q, т.е. подтверждается нулевая гипотеза о постоянстве центра группирования. Следовательно, условия измерений для приведенного ряда оставались неизменными, и систематических расхождений между результатами наблюдений нет.

Задача

Используя способ последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений, приведенных в таблице 3.3.

№ вари-анта	U, В
12,38	11,97	12,34	11,46	11,75	12,05
11,88	11,81	14,05	12,33	12,45
12,07	11,78	11,23	11,91	11,74
12,91	12,88	12,99	13,09	13,33	13,43
13,72	13,06	12,76	13,23	10,57
11,98	12,78	12,95	13,07	13,25
3٭	14,38	14,44	14,32	14,21	13,78	14,22	13,59	14,21	13,77
13,88	14,01	13,67	14, 09	13,06	13,69	13,89	13,75
4٭	14,88	14,43	15,79	14,66	15,34	14,99
15,21	16,98	15,57	14,69	15,32	15,27
15,36	14,45	14,79	15,37	15,01
16,31	16,02	15,58	15,88	15,92	16,01	15,88	15,82	15,94
16,69	16,09	15,97	15,94	16,01	16,04	15,69	15,87
6٭	17,09	17,35	17,34	16,99	16,85	17,21	17,11	16,44
17,22	16,81	17,72	17,15	17,25	17,89	17,13	17,09
18,11	18,21	18,32	18,41	17,88	17,67	17,79
17,91	17,67	18,25	18,32	15,44	17,98	18,44
18,24	18,12	18,28	18,22	17,93	17,86
19,09	19,03	18,77	18,98	18,75	19,36
18,66	16,88	18,71	19,61	19,49	19,22
18,83	18,79	19,29	19,74	19,33
9٭	19,98	19,89	20,03	20,14	20,28	19,84	20,08	20,23
19,99	19,83	20,33	20,11	19,76	22,16	20,41	20,77
21,09	20,87	21,33	21,34	21,21	20,09
21,04	21,24	21,24	21,22	21,19	21,41
21,13	20,67	20,94	21,12	21,19
22,12	22,28	22,44	24,06	21,75	21,32
21,88	21,81	22,33	22,45	22,02	21,97
21,91	22,07	22.34	21,74	21,46	21,32
22,75	22,87	22,29	23,43	23,33
23,72	23,06	23,23	20,57	22,96
22,98	21,99	27,07	23,25	23,09
24,38	23,96	23,59	23,75	24,07
24,29	24,35	23,97	26,05	23,77
23,78	23,69	24,21	23,93	24,44
14٭	25,79	24,93	25,03	24.88	25,29	25,11	24,99	24,79
25,02	25,06	24,95	25,13	26,98	24,68	25,08	25,03
Продолжение табл.3.3
28,88	25,82	25,87	25,97	26,55	26,11	26,31	26,09	25,88
25,69	25,92	25,94	24,09	26,02	26,88	26,69	25,58
27,09	26,77	27,22	26,93	24,69	26,44	26,96	26,85
26,91	26,89	26,76	27,72	27,22	27,08	26,81	27,09
17	28,24	27,88	28,85	25,43	27,67	27,86	28,44	28,22
28,32	28,12	27,93	28,41	28,32	28,21	28,11	27,91
29,74	28,83	28,66	29,03	29,29	28,71	29,61	29,33	29,36
28,98	29,09	28,79	26,88	28,77	28,75	29,49	29,22	28,77
19٭	29,88	29,99	30,11	30,34	30,28	30,33	30,06	32,16
30,12	30,01	29,95	29,78	30,05	30,12	30,13	30,03
20٭	31.113	31,27	31,20	31,19	30,52	31,17	31,23	31,07	31,18
31,25	31,01	30,24	30,66	30,48	31,33	30,09	28,76	31,12

4. Вероятностное описание случайных погрешностей

Когда при проведении в одинаковых условиях повторных измерений одной и той же постоянной величины получаем результаты, отличающиеся друг от друга, это свидетельствует о наличии в них случайных погрешностей. Эта погрешность возникает вследствие одновременного воздействия на результат многих случайных возмущений и сама является случайной величиной. Для установления вероятностных (статистических) закономерностей появления случайных погрешностей и количественной оценки результата измерений и его случайной погрешности используются методы теории вероятностей и математической статистики.

Для характеристики свойств случайной величины в теории вероятностей используют понятие закона распределения вероятностей случайной величины. В метрологии преимущественно используется дифференциальная форма – закон распределения плотности вероятностей случайной величины.

Рассмотрим формирование дифференциального закона.

1. Проведем n измерений одной величины Х.

2. Получим группу наблюдений х₁; х_2,…,х_n.

3. Расположим результаты в порядке возрастания от х_min до х_max.

4. Найдем размах ряда L=х_max — х_min.

5. Разделим размах ряда на k равных интервалов ∆l=L/k.

6. Подсчитаем количество наблюдений n_k, попадающих в каждый интервал.

7. Изобразим полученные результаты графически (по оси абсцисс – значения физической величины с границами интервалов; по оси ординат – относительная частота попаданий n_k/n).

8. Достроив по полученным точкам соответствующие прямоугольники, получим гистограмму (рис.4.1), дающую представление о плотности распределения результатов наблюдений в данном опыте.

Пример 4.1. Построить гистограмму по данным приведенным ниже.

n=50 измерений.

№ интервала
nk
nk/n	0,1	0,2	0,36	0,22	0,12

Если распределение случайной величины статистически устойчиво, то можно ожидать, что при повторных сериях наблюдений той же величины в тех же условиях, относительные частоты попаданий в каждый интервал будут близки к первоначальным. Следовательно, по гистограмме можно предсказывать распределение результатов измерений по интервалам.

При бесконечном увеличении числа наблюдений n→∞ и бесконечном уменьшении ширины интервалов Δl→0, ступенчатая кривая, огибающая гистограмму, перейдет в плавную кривую f(x), которая называется кривой плотности распределения вероятностей случайной величины (рис.4.2), а уравнения ее описывающие дифференциальным законом распределения.

Рис.4.2. Кривая плотности распределения вероятностей

Кривая плотности распределения вероятностей всегда неотрицательна и подчинена условию нормирования в виде:

. (4.1)

Если известен закон распределения случайной величины f(x), то вероятность Р ее попадания в интервал от х₁ до х₂ :

. (4.2)

Числовые характеристики случайных величин вычисляются по следующим формулам:

· среднее арифметическое значение исправленных результатов наблюдений , которое принимается за результат измерения, если подтверждается гипотеза о нормальном распределении результатов наблюдений и ряд наблюдений не содержит промахов:

; (4.3)

· смещенная (S * ) и несмещенная (S) среднеквадратическая погрешность ряда измерений

; (4.4)

. (4.5)

· среднеквадратическая погрешность среднеарифметического значения:

. (4.6)

Методика проверки гипотезы о том, что результаты наблюдений распределены нормально, зависит от числа наблюдений:

— если n≥50, используют критерий χ 2 Пирсона;

— если 15 Z_q)=q. Значения Z_q приведены в таблице 5.2.

Источник

Способы обнаружения и устранения систематических погрешностей

Результаты наблюдений, полученные при наличии систематической погрешности, называются неисправленными. При проведении измерений стараются в максимальной степени исключить или учесть влияние систематических погрешностей.

Это может быть достигнуто следующими путями:

— устранением источников погрешностей до начала измерений. В большинстве областей измерений известны главные источники систематических погрешностей и разработаны методы, исключающие их возникновение или устраняющие их влияние на результат измерения. В связи с этим в практике измерений стараются устранить систематические погрешности не путем обработки экспериментальных данных, а применением СИ, реализующих соответствующие методы измерений;

— определением поправок и внесением их в результат измерения;

— оценкой границ неисключенных систематических погрешностей.

Постоянная систематическая погрешность не может быть найдена методами совместной обработки результатов измерений. Однако она не искажает ни показатели точности измерений, характеризующие случайную погрешность, ни результат нахождения переменной составляющей систематической погрешности. Действительно, результат одного измерения

где x_и — истинное значение измеряемой величины; _i — i-я случайная погрешность; _i — i-я систематическая погрешность. После устранения результатов многократных измерении получаем среднее арифметическое значение измеряемой величины

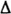
Если систематическая погрешность постоянна во всех измерениях, т.е. _i= ,то

Таким образом, постоянная систематическая погрешность не устраняется при многократных измерениях.

Постоянные систематические погрешности могут быть обнаружены лишь путем сравнения результатов измерений с другими, полученными с помощью более высокоточных методов и средств. Иногда эти погрешности могут быть устранены специальными приемами проведения процесса измерений. Эти методы рассмотрены ниже.

Наличие существенной переменной систематической погрешности искажает оценки характеристик случайной погрешности и аппроксимацию ее распределения. Поэтому она должна обязательно выявляться и исключаться из результатов измерений.

Для устранения постоянных систематических погрешностей применяют следующие методы:

— Метод замещения, представляющий собой разновидность метода сравнения, когда сравнение осуществляется заменой измеряемой величины известной величиной, причем так, что при этом в состоянии и действии всех используемых средств измерений не происходит никаких изменений. Этот метод дает наиболее полное решение задачи. Для его реализации необходимо иметь регулируемую меру, величина которой однородна измеряемой. Например, взвешивание по методу Борда, измерение сопротивления посредством моста постоянного тока и мер сопротивления.

— Метод противопоставления, являющийся разновидностью метода сравнения, при котором измерение выполняется дважды и проводится так, чтобы в обоих случаях причина постоянной погрешности оказывала разные, но известные по закономерности воздействия на результаты наблюдений. Например, способ взвешивания Гаусса.

— Метод компенсации погрешности по знаку (метод изменения знака систематической погрешности), предусматривающий измерение с двумя наблюдениями, выполняемыми так, чтобы постоянная систематическая погрешность входила в результат каждого из них с разными знаками.

— Метод рандомизации — наиболее универсальный способ исключения неизвестных постоянных систематических погрешностей. Суть его состоит в том, что одна и та же величина измеряется различными методами (приборами). Систематические погрешности каждого из них для всей совокупности являются разными случайными величинами. -Вследствие этого при увеличении числа используемых методов (приборов) систематические погрешности взаимно компенсируются.

Для устранения переменных и монотонно изменяющихся систематических погрешностей применяют следующие приемы и методы.

— Анализ знаков неисправленных случайных погрешностей.

Если знаки неисправленных случайных погрешностей чередуются с какой-либо закономерностью, то наблюдается переменная систематическая погрешность. Если последовательность знаков «+» у случайных погрешностей сменяется последовательностью знаков «-» или наоборот, то присутствует монотонно изменяющаяся систематическая погрешность. Если группы знаков «+» и «-» у случайных погрешностей чередуются, то присутствует периодическая систематическая погрешность.

— Графический метод.

Он является одним из наиболее простых способов обнаружения переменной систематической погрешности в ряду результатов наблюдений и заключается в построении графика последовательности неисправленных значений результатов наблюдений. На графике через построенные точки проводят плавную кривую, которая выражает тенденцию результата измерения, если она существует. Если тенденция не прослеживается, то переменную систематическую погрешность считают практически отсутствующей.

— Метод симметричных наблюдений.

Рассмотрим сущность этого метода на примере измерительного преобразователя, передаточная функция которого имеет вид y = kx + y₀ , где х, у — входная и выходная величины преобразователя; k — коэффициент, погрешность которого изменяется во времени по линейному закону; у₀ — постоянная.
Для устранения систематической погрешности трижды измеряется выходная величина у через равные промежутки времени At. При первом и третьем измерениях на вход преобразователя подается сигнал х0 от образцовой меры. В результате измерений получается система уравнений:

Ее решение позволяет получить значение х, свободное от переменной систематической погрешности, обусловленной изменением коэффициента k:

Специальные статистические методы. К ним относятся способ последовательных разностей, дисперсионный анализ, и др. Рассмотрим подробнее некоторые из них.

Способ последовательных разностей (критерий Аббе).

Применяется для обнаружения изменяющейся во времени систематической погрешности и состоит в следующем. Дисперсию результатов наблюдений можно оценить двумя способами: обычным

и вычислением суммы квадратов последовательных (в порядке проведения измерений) разностей ( x_i+1 — x_i) 2

Если в процессе измерений происходило смещение центра группирования результатов наблюдений, т.е. имела место переменная систематическая погрешность, то 2 [x] дает преувеличенную оценку дисперсии результатов наблюдений. Это объясняется тем, что на 2 [x] влияют вариации . В то же время изменения центра группирования весьма мало сказываются на значениях последовательных разностей d _i = x _i+1-x _i, поэтому смещения почти не отразятся на значении Q 2 [x].

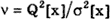
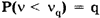
Отношение является критерием для обнаружения систематических смещений центра группирования результатов наблюдений. Критическая область для этого критерия (критерия Аббе) определяется как , где q = 1-Р — уровень значимости, Р — доверительная вероятность. Значения v_q для различных уровней значимости q и числа наблюдений n приведены в таблице. Если полученное значение критерия Аббе меньше при заданных q и n, то гипотеза о постоянстве центра группирования результатов наблюдений отвергается, т.е. обнаруживается переменная систематическая погрешность результатов измерений.

n	vq при q, равном	n	vq при q, равном
0.001	0.01	0.05	0.001	0.01	0.05
0.295	0.313	0.390	0.295	0.431	0.578
0.208	0.269	0.410	0.311	0.447	0.591
0.182	0.281	0.445	0.327	0.461	0.603
0.185	0.307	0.468	0.341	0.474	0.614
0.202	0.331	0.491	0.355	0.487	0.624
0.221	0.354	0.512	0.368	0.499	0.633
0.241	0.376	0.531	0.381	0.510	0.642
0.260	0.396	0.548	0.393	0.520	0.650
0.278	0.414	0.564

Дисперсионный анализ (критерий Фишера).

В практике измерений часто бывает необходимо выяснить наличие систематической погрешности результатов наблюдений, обусловленной влиянием какого-либо постоянно действующего фактора, или определить, вызывают ли изменения этого фактора систематическое смещение результатов измерений. В данном случае проводят многократные измерения, состоящие из достаточного числа серий, каждая из которых соответствует определенным (пусть неизвестным, но различным) значениям влияющего фактора. Влияющими факторами, по которым производится объединение результатов наблюдений по сериям, могут быть внешние условия (температура, давление и т.д.), временная последовательность проведения измерений и т.п.

После проведения N измерений их разбивают на s серий (s > 3) по n_j результатов наблюдений ( sn_j = N ) в каждой серии и затем устанавливают, имеется или отсутствует систематическое расхождение между результатами наблюдений в различных сериях. При этом должно быть установлено, что результаты в сериях распределены нормально. Рассеяние результатов наблюдений в пределах каждой серии отражает только случайные влияния, характеризует лишь случайные погрешности измерений в пределах этой серии. Характеристикой совокупности случайных внутрисерийных погрешностей будет средняя сумма дисперсий результатов наблюдений, вычисленных раздельно для каждой серии, т.е.

где x_ji — результат i-го измерения в j-й серии.
Внутрисерийная дисперсия 2 _BC характеризует случайные погрешности измерений, так как только случайные влияния обусловливают те различия (отклонения результатов наблюдений), на которых она основана. В то же время рассеяние _j различных серий обусловливается не только случайными погрешностями измерений, но и систематическими различиями (если они существуют) между результатами наблюдений, сгруппированными по сериям. Следовательно, усредненная межсерийная дисперсия

где , выражает силу действия фактора, вызывающего систематические различия между сериями.

Таким образом, 2 _BC /( 2 _BC + 2 _MC) характеризует долю дисперсии всех результатов наблюдений, обусловленную наличием случайных погрешностей измерений, а 2 _MC /( 2 _BC + 2 _MC) — долю дисперсии, обусловленную межсерийными различиями результатов наблюдений. Первую из них называют коэффициентом ошибки, вторую — показателем дифференциации. Чем больше отношение показателя дифференциации к коэффициенту ошибки, тем сильнее действие фактора, по которому группировались серии, и тем больше систематическое различие между ними.

Критерием оценки наличия систематических погрешностей в данном случае является дисперсионный критерий Фишера F = 2 _MC 2 _BC. Критическая область для критерия Фишера соответствует P (F>F_q) = q.

Значения F_q для различных уровней значимости q, числа измерений N и числа серий s приведены в приложении 1, где k₂ = N-s , k₁ = s-1. Если полученное значение критерия Фишера больше F_q (при заданных q, N и s), то гипотеза об отсутствии систематических смещений результатов наблюдений по сериям отвергается, т.е. обнаруживается систематическая погрешность, вызываемая тем фактором, по которому группировались результаты наблюдений.

Из всех рассмотренных способов обнаружения систематических погрешностей дисперсионный анализ является наиболее эффективным и достоверным, так как позволяет не только установить факт наличия погрешности, но и дает возможность проанализировать источники ее возникновения.

Если закон распределения результатов измерений неизвестен, то для обнаружения систематической погрешности применяют статистический критерий Вилкоксона.

Из двух групп результатов измерений x₁, x₂. x_n и y₁, y₂. y_m , n> = m> = 5 , составляется вариационный ряд, в котором все n + m значений x₁, x₂. x_n и y₁, y₂. y_m располагают в порядке их возрастания и приписывают им ранги — порядковые номера членов вариационного ряда. Различие средних значений каждого из рядов можно считать допустимым, если выполняется неравенство

где R_i — ранг (номер) члена x_i, равный его номеру в вариационном ряду T — _q и T + _q — нижнее и верхнее критические значения для выбранного уровня значимости q.

При mm>15 они рассчитываются по формулам:

где z_p — квантиль нормированной функции Лапласа.

Таблица. Критические значения T_q — и T_q + при q=0.05 и 0,01

n	m	q=0.05	q=0.01
Tq —	Tq +	Tq —	Tq +

Исключение систематических погрешностей путем введения поправок.

В ряде случаев систематические погрешности могут быть вычислены и исключены из результата измерения. Для этого используются поправки. Поправка C_j — величина, одноименная измеряемой, которая вводится в результат измерения x_i = x_i ‘ + _j + C_j с целью исключения составляющих систематической погрешности _j. При C_j = —_j j-я составляющая систематической погрешности полностью устраняется из результата измерения. Поправки определяются экспериментально или в результате специальных теоретических исследований. Они задаются в виде таблиц, графиков или формул.

Введением одной поправки устраняется влияние только одной составляющей систематической погрешности. Для устранения всех составляющих в результат измерения приходится вводить множество поправок. При этом вследствие ограниченной точности определения поправок случайные погрешности результата измерения накапливаются и его дисперсия увеличивается. Так как поправка известна с определенной точностью, то она характеризуется статистически — средним значением поправки С и СКО S_c. При исправлении результата x_i ‘ путем введения поправок C_j , где j = l, 2. m, по формуле

дисперсия исправленного результата

где S_н 2 — оценка дисперсии неисправленного результата; S_cj 2 — оценка дисперсии j-й поправки. Как видно, с одной стороны, уточняется результат измерения, а с другой — увеличивается разброс за счет роста дисперсии. Следовательно, необходимо найти оптимум.
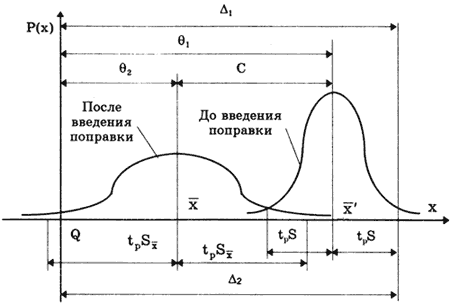
Пусть при измерении постоянной величины Q получено значение Q = ‘ t _pS ,где — оценка среднего арифметического неисправленного результата измерений; t_p — коэффициент Стьюдента.

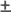
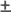
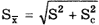
После введения поправки C t_pS_c результат измерения

где .
Максимальные доверительные значения погрешности результата измерения до и после введения поправки равны соответственно

Поправку имеет смысл вводить до тех пор, пока 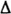₁ 0.5S_c 2 /S 2 . Из этого неравенства видно, что если оценка среднего квадратического отклонения поправки S_c стремится к нулю, то поправку имеет смысл вводить всегда. В практических расчетах погрешность результата обычно выражается не более чем двумя значащими цифрами, поэтому поправка, если она меньше пяти единиц младшего разряда, следующего за последним десятичным разрядом погрешности результата, все равно будет потеряна при округлении и вводить ее не имеет смысла.

Источник