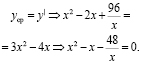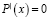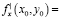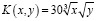Использование математических способов анализа

Математические методы экономического анализа

Вы будете перенаправлены на Автор24

Понятие математических методов экономического анализа

При аналитическом изучении деятельности предприятия используются математические методы исследования. Данные методы позволяют расширить изучение факторов, влияющих на хозяйственную деятельность организации, что в свою очередь позволит увеличить количество резервов повышения качества. Внедрение методов на современном этапе позволяет определить потребность оперативного вмешательства и прогнозирования возможных исходов, а это практически невозможно без аналитического исследования.

Под экономическим анализом понимают прикладную научную дисциплину, представляющую собой систему специальных знаний, позволяющих оценить эффективность деятельности того или иного субъекта рыночной экономики.

Виды методов экономического анализа

Условно методы экономического анализа делят на математические и традиционные. Под традиционными методами принято понимать оценку функциональной зависимости, которая возникает между показателями. Математические методы используются при анализе стохастической системы.

Математические методы помогают выявить более точные результаты и создают подробную картину воздействия факторов на деятельность организации. В совокупности это ускоряет процесс экономического анализа. Для того, чтобы использовать математические методы необходимо:

• разработать математическую модель;
• учесть взаимосвязь между объектами;
• использовать системный подход;
• усовершенствовать систему благодаря информационному обеспечению.

Задачи экономического анализа возможно решить математическим методом только в том случае, если их формулировка имеет математический вид. Другими словами, все взаимосвязи выражены при помощи математического анализа.

Готовые работы на аналогичную тему

К математическому методу относят:

• методы экономической кибернетики;
• методы математического программирования;
• методы элементарной математики;
• методы математической статистики;
• эконометрические методы;
• методы исследования операций;
• классические методы математического анализа;
• метод теории оптимальных процессов.

Данная классификация условна, так в зависимости от организации и необходимого результата используют различные вариации.

Метод экономической кибернетики используют при анализе сложных систем. Наиболее используемые методы в этой области — это метод системного анализа и моделирования.

Для оптимизации хозяйственных процессов организации используют метод математического программирования. Данный метод позволяет дифференцировать результат, определить уровень поставленной задачи и выявить лимитирующие группы сырья и оборудования.

Традиционные расчеты ресурсов при разработке и планировании на предприятии относят к методам элементарной математики.

Методы статистики используют в массовых явлениях. Данный метод позволяет проанализировать возможные изменения показателей. В случае выявления между исследуемыми характеристиками стохастической связи, только статистические методы позволяют провести анализ.

Эконометрический метод основывается на трех составляющих: математика, статистика и экономика. В основе данного метода лежит эконометрическая модель. Другими словами, процесс или явление представляет собой схематическое представление. Данные модели построены по шахматной схеме и используется для выявления связи между затратами и результатом.

Для того, чтобы разработать и оценить наилучший вариант действий, используют методы исследования операций. Данные методы позволяют выбрать наилучший показатель из возможных.

Классические методы математического исследования используют как в совокупности с другими методами, так и отдельно.

Метод теории оптимальных процессов направлен на построение системы, которая сведет к минимуму функционал поставленной задачи и определит точное решение.

Источник

Использование математических способов анализа

Математические методы все большее применение находят в анализе экономической деятельности организаций. В результате их использования становится возможным исследование влияния отдельных факторов на экономические показатели деятельности предприятий разного уровня собственности, что способствует уменьшению сроков анализа этой деятельности, повышению точности осуществления экономических расчетов. С помощью математических методов становится возможным решение многомерных аналитических задач, которые не могут быть выполнены традиционными методами. В процессе использования методов математического анализа осуществляется построение и изучение экономико-математических моделей, описывающих влияние отдельных факторов на экономические показатели деятельности организаций.

В большинстве литературных источников [1, 2] под экономико-математической моделью понимают математическое описание экономического объекта или процесса с целью их исследования и управления ими. Это математическая запись решаемой экономической задачи.

Остановимся на использовании математического анализа в моделировании экономических процессов. Для наглядного изображения зависимостей между экономическими величинами широкое применение находят функции. С помощью функций и функциональных зависимостей моделируются взаимосвязи между различными величинами, количественные и качественные отношения между различными экономическими характеристиками и показателями. Набор используемых функций весьма широк: от простейших линейных до функций, зависящих от нескольких переменных, определяющих состояния изучаемых объектов в разные периоды времени. В экономике наиболее часто используются следующие функции: функция полезности, производственная функция, функция спроса, потребления и предложения [3, 4].

Функция полезности (функция предпочтения) задает зависимость результата, эффекта некоторого действия от уровня (интенсивности) этого действия.

Производственная функция устанавливает зависимость результата производственной деятельности от обусловивших его факторов. Производственная функция характеризует техническую зависимость между ресурсами и выпуском и описывает всю совокупность технологически эффективных способов.

С помощью функции потребления, спроса и предложения определяется зависимость объема потребления, спроса и предложения на отдельные товары или услуги от различных факторов (например, цены, дохода и т.п.).

Все перечисленные выше функции чаще всего зависят не от одной переменной, а от нескольких переменных. Поэтому геометрическое представление данных зависимостей затруднено. В более простых случаях графики функции полезности, производственной функции, функции спроса, потребления и предложения, а также анализ зависимостей экономических переменных можно найти в [5]. В своем исследовании мы остановимся на приложении классических методов математического анализа, которые используются как самостоятельно (дифференцирование и интегрирование), так и в рамках других методов. Остановимся на методе, который основывается на определении производной и её приложениях. Рассмотрим сначала функцию одной переменной 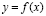. 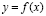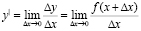С точки зрения математического анализа производной функции называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):

.

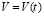
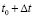
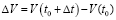
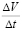
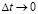
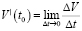
Экономический смысл производной может быть получен при рассмотрении понятий производительности труда, издержек производства и т.п. Проведем соответствующие рассуждения на примере задачи о производительности труда. Пусть функция выражает зависимость объема V произведенной продукции от времени t. Требуется найти производительность труда в момент времени t0. Объем произведенной продукции с момента времени t0 до составит . Величина есть средняя производительность за этот период времени. Тогда производительность труда в момент времени t0 можно определить как предельное значение средней производительности при :

.

Получаем экономический смысл производной: производная объема произведенной продукции по времени 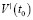есть производительность труда в момент времени t0.

Если мы рассмотрим задачу про издержки производства, то формула

,

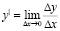
где издержки производства y есть функция количества выпускаемой продукции х, выражает предельные издержки производства и характеризует приближенно дополнительные затраты на производство единицы дополнительно продукции.

Аналогичным образом определяются предельная выручка, предельный продукт, предельная полезность и другие предельные величины. Применение дифференциального исчисления для исследования экономических процессов на основе анализа предельных величин получило название предельного анализа. Таким образом, предельные величины характеризуют процесс изменения экономического объекта, т.е. производная выступает как скорость изменения некоторого экономического процесса по времени или относительно другого исследуемого фактора.

Пример 1. Функция полных затрат в зависимости от объема выпускаемой продукции задана соотношением 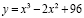. При каком объеме производства предельные и средние затраты совпадают?

Решение. Средние затраты вычисляются по формуле

.

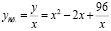
Для нахождения предельных затрат воспользуемся экономическим смыслом производной 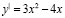. Значение х, при котором предельные и средние затраты совпадают, находим из уравнения:

Решая последнее уравнение, найдем значение 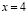. Таким образом, предельные и средние затраты совпадают при объеме производства равном 4.

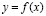
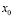
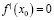
При решении экономических задач часто используется известная теорема Ферма, которая утверждает, что если дифференцируемая на некотором промежутке функция достигает наибольшего или наименьшего значения во внутренней точке этого промежутка, то производная функции в этой точке равна нулю, т.е. .

Экономической интерпретацией теоремы Ферма является базовый закон теории производства, который утверждает, что оптимальный для производителя уровень выпуска товара определяется равенством предельных издержек и предельного дохода.

Пример 2. Найти максимальную прибыль, которую может получить фирма-производитель, при условии, что весь товар реализуется по фиксированной цене р=10,5 за единицу, а функция издержек имеет вид

.

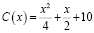
Решение. Так как х количество производимого товара, то доход фирмы выражается формулой:

.

,

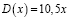
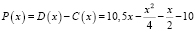
т.е. .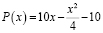

Найдем производную и точки, подозрительные на экстремум:

;

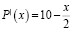
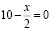
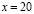
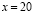
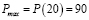
тогда и только тогда, когда , т.е. . Исследуя знак производной в окрестности точки , заключаем, что она является точкой максимума. Значит . Следовательно, максимальная прибыль фирмы равна 90 ден. ед.

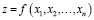
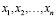
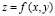
В экономической теории очень часто встречаются задачи, в которых используются функции нескольких переменных. Примерами таких функций являются: функция полезности от п приобретенных товаров; производственная функция, выражающая результат производственной деятельности от обусловивших его факторов . Мы остановимся на рассмотрении случая функции двух переменных . Для решения экономических задач, содержащих в условии функции двух переменных, требуется знание понятия частных производных по переменным х и у первого и второго порядков, необходимое и достаточное условия экстремума.

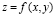
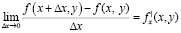
Напомним, что частной производной функции по независимой переменной х называется конечный предел

.

Аналогично производной по переменной у называется предел

.

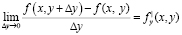
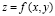
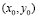
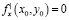
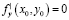
Необходимым условием существования экстремума дифференцируемой функции в точке является равенство нулю её частных производных: и .

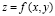
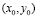
Для того чтобы функция имела экстремум в точке , достаточно выполнения следующих условий:

существования непрерывных частных производных второго порядка в окрестности точки ;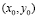

;

,

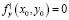
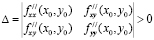
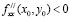
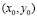
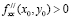
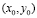
причем, если , то – точка максимума, если , то – точка минимума.

Пример 3. Найти величины используемых ресурсов (х, у), при которых фирма-производитель получит максимальную прибыль, если заданы производственная функция

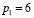
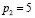
и цены ден. ед. и ден. ед. первого и второго ресурсов.

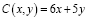
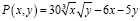
Решение. Производственная функция в денежном выражении равна доходу от использования ресурсов. При этом издержки . Функция прибыли имеет вид:

.

Найдем её максимум.

.

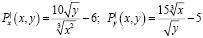
Решая систему уравнений

найдем стационарную точку (125, 225). Исследуем её на экстремум:

следовательно, (125, 225) – точка экстремума; 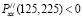, следовательно, (125, 225) – точка максимума. Таким образом, максимальная прибыль будет при х=125, у=225.

Из рассмотренных задач можно сделать вывод, что методы математического анализа и в частности дифференциальное исчисление широко применяются для решения экономических задач. Математический анализ позволяет выявить резервы повышения эффективности производства. Роль анализа в управлении производством возрастает вследствие того, что меняется механизм хозяйствования, меняются принципы и методы управления. Ограниченность ресурсов и необходимость выбора заставляют руководителей постоянно проводить исследования в области рынков сбыта, источников сырья, изучения спроса, ценообразования, что должно обеспечить повышение эффективности производства.

Источник