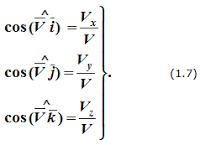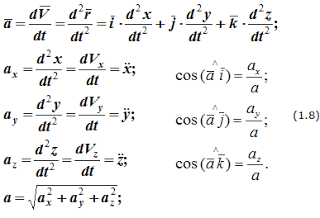Исходными данными при координатном способе задания движения точки являются

iSopromat.ru

При координатном способе задания движения точки в выбранной системе координат задаются координаты движущейся точки как функции от времени.

В прямоугольной декартовой системе координат это будут уравнения:

Эти уравнения являются и уравнениями траектории в параметрической форме. Исключая из этих уравнений параметр t, можно получить три пары систем двух уравнений, каждая из которых представляет траекторию точки, как пересечение поверхностей.

Кроме декартовых могут быть использованы другие системы координат (сферическая, цилиндрическая). Всегда можно перейти от координатного способа задания движения к векторному (рисунок 1.3):

Поэтому, используя формулы для определения скорости и ускорения точки при векторном способе задания движения, можно получить аналогичные формулы для координатного способа:

Направление вектора скорости определяется с помощью направляющих косинусов:

Формулы (1.6) и (1.7) полностью определяют вектор скорости при координатном способе задания движения точки, т.е. по величине и направлению.

Аналогичны формулы для определения ускорения точки:

Формулы (1.8) определяют величину и направление вектора ускорения. В формулах (1.6) и (1.8) приведены используемые в различных учебниках обозначения проекций скоростей и ускорений точек на оси декартовой системы координат.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Координатный способ задания движения точки

Введение

Выводы приведенных ниже формул и изложение теории приводится на странице “Кинематика материальной точки”. Здесь мы применим основные результаты этой теории к координатному способу задания движения материальной точки.

Пусть мы имеем неподвижную прямоугольную систему координат с центром в неподвижной точке . При этом положение точки M однозначно определяются ее координатами (x, y, z). Координатный способ задания движения точки – это такой способ, при котором заданы зависимости координат от времени. То есть заданы три функции от времени (при трехмерном движении):

Далее мы приводим формулы вычисления кинематических величин и пример решения задачи для координатного способа задания движения.

Определение кинематических величин

Зная зависимости координат от времени , мы автоматически определяем радиус-вектор материальной точки M по формуле:
,
где – единичные векторы (орты) в направлении осей x, y, z .

Дифференцируя по времени , находим проекции скорости и ускорения на оси координат:
;
;
Модули скорости и ускорения:
;
.

Единичный вектор в направлении касательной к траектории:
.
Его можно определить двумя способами – по направлению скорости, или в противоположную сторону. Поэтому здесь в знаменателе стоит не модуль скорости, а алгебраическая величина скорости, которая, по абсолютной величине, равна модулю скорости, но может принимать как положительные, так и отрицательные значения: . Она является проекцией скорости на направление единичного вектора .

Алгебраическая величина тангенциального (касательного) ускорения – это проекция полного ускорения на направление единичного вектора касательной к траектории:
.
Вектор тангенциального (касательного) ускорения:
.
Здесь также, как и для скорости, – это скалярная величина, которая может принимать как положительные так и отрицательные значения: .

Нормальное ускорение:
.
Вектор нормального ускорения:
; .
Единичный вектор в направлении главной нормали траектории (то есть единичный вектор, перпендикулярный касательной и направленный к центру кривизны траектории):
.
Здесь – это модуль нормального ускорения: . Нормальное ускорение всегда направлено к центру кривизны траектории. Оно не может быть направлено в противоположную сторону.

Радиус кривизны траектории:
.
Центр кривизны траектории:
.

Единичный вектор в направлении бинормали:
.

Пример решения задачи

Определение скорости и ускорения точки по заданным уравнениям ее движения

По заданным уравнениям движения точки установить вид ее траектории и для момента времени найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.

Уравнения движения точки:
, см;
, см.

Решение

Определение вида траектории

Исключаем время из уравнений движения. Для этого перепишем их в виде:
; .
Применим формулу:
.
;
;
;
.

Итак, мы получили уравнение траектории:
.
Это уравнение параболы с вершиной в точке и осью симметрии .

Поскольку
, то
; или
.
Аналогичным образом получаем ограничение для координаты :
;
;

Таким образом, траекторией движения точки является дуга параболы
,
расположенная при
и .

Строим параболу по точкам.

0	6
± 3	5,625
± 6	4,5
± 9	2,625
± 12	0

Определяем положение точки в момент времени .
;
.

Определение скорости точки

Дифференцируя координаты и по времени , находим компоненты скорости.
.
Чтобы продифференцировать , удобно применить формулу тригонометрии:
. Тогда
;
.

Вычисляем значения компонент скорости в момент времени :
;
.
Модуль скорости:
.

Определение ускорения точки

Дифференцируя компоненты скорости и по времени , находим компоненты ускорения точки.
;
.

Вычисляем значения компонент ускорения в момент времени :
;
.
Модуль ускорения:
.

Алгебраическая величина тангенциального ускорения – это проекция полного ускорения на направление единичного вектора касательной к траектории. Выберем направление совпадающим с направлением скорости . Тогда ; алгебраическая величина тангенциального ускорения – это проекция полного ускорения на направление скорости :
.
Поскольку , то вектор тангенциального ускорения направлен противоположно скорости .

Нормальное ускорение:
.
Вектор и направлен в сторону центра кривизны траектории.

Радиус кривизны траектории:
.

Траекторией движения точки является дуга параболы
; .
Скорость точки: .
Ускорение точки: ; ; .
Радиус кривизны траектории: .

Определение остальных величин

При решении задачи мы нашли:
вектор и модуль скорости:
; ;
вектор и модуль полного ускорения:
; ;
тангенциальное и нормальное ускорения:
; ;
радиус кривизны траектории: .

Определим остальные величины.

Единичный вектор в направлении касательной к траектории:
.
Вектор тангенциального ускорения:

.
Вектор нормального ускорения:

.
Единичный вектор в направлении главной нормали:
.
Координаты центра кривизны траектории:

.

Введем третью ось системы координат перпендикулярно осям и . В трехмерной системе
; .
Единичный вектор в направлении бинормали:

.

Автор: Олег Одинцов . Опубликовано: 22-02-2016 Изменено: 29-01-2020

Источник

Координатный способ задания движения точки.

В этом случае положение движущейся точки в пространстве определяют тремя ее декартовыми координатами относительно выбранной неподвижной прямоугольной системы осей (рис. 41). При движении точки эти координаты являются однозначными и непрерывными функциями времени, т.е. уравнения движения получают в виде:

, , (14)

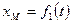
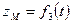
При координатном способе задания движения точки, траектория в непосредственном виде не дается, но может быть получена из уравнений движения. Исключая из уравнений движения время, получаем два соотношения между координатами 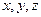, которые определяют линию, описываемую в пространстве движущейся точкой, т.е. ее траекторию.

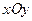
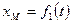
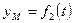
Если движущаяся точка остается за все время движения в одной и той же плоскости, то, приняв эту плоскость за координатную , получаем два уравнения движения , .

Уравнения движения точки в координатной форме представляют собой уравнение траектории в параметрической форме, где за независимый параметр принято время. Исключая его из уравнений движения, получаем уравнение траектории.

При движении точки в плоскости можно пользоваться не только декартовыми координатами. В этом случае можно ввести в рассмотрение полярные координаты (рис. 42).

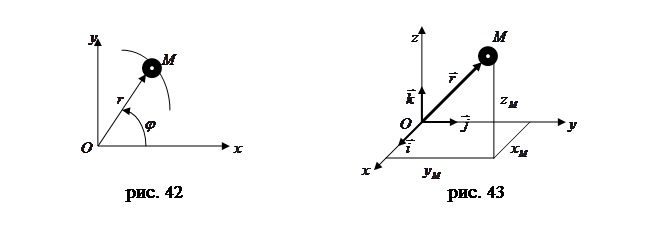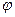
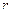
Положение точки в этом случае будут определять полярный угол и вектор , т.е. уравнения движения точки в полярных координатах имеют вид: .

Векторный способ задания движения точки.

В этом случае положение точки в пространстве определяется только радиусом – вектором, проведенным из начала декартовой системы координат (рис. 43). Уравнение движения в этом случае имеет вид:

(15)

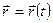
Векторный способ задания движения удобен для установления общих зависимостей, так как позволяет описать движение точки одним векторным уравнением вместо трех скалярных.

Источник

iSopromat.ru

Рассмотрим три существующих способа задания движения материальной точки: координатный, векторный и естественный.

Чтобы иметь возможность определить параметры движения точки необходимо задать закон ее движения.

В зависимости от известных величин и поставленной задачи могут быть использованы следующие способы задания движения точки: векторный, координатный и естественный.

Векторный

При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.

Координатный

При координатном способе задания движения задаются координаты точки как функции времени:

Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t. Чтобы записать ее уравнение в явной форме, надо исключить из них t.

Естественный

При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t). Этим способом удобно пользоваться, если траектория точки заранее известна.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Координатный способ задания движения точки.

Рис. 2.2. Координатный способ

В этом случае с неподвижной точкой связывается декартовая система координат, и положение движущейся точки задается скалярными функциями времени ее декартовых координат (рис. 2.2). (2.2)

Естественный способ задания движения точки.В случае, когда траектория движения точки известна заранее более выгодным является использование в качестве системы отсчета точки на траектории, а положение движущейся точки характеризовать дуговой координатой s(t) (рис. 2.3) – алгебраической величиной – расстоянием, отсчитываемым по траектории от неподвижной точки с определенным знаком. Таким образом, здесь задается:

Рис. 2.3 ‑ Естественный способ

а) траектория точки, б) начало отсчета, в) направление положительного и отрицательного отсчета дуговой координаты, г) зависимость дуговой координаты от времени (2.3)

Скорость точки. Определение скорости в различных способах задания движения точки.Для характеристики быстроты изменения положения точки введем кинематическую характеристику – скорость точки. Определим ее для всех трех видов задания движения точки.

Векторный способ.Из рис. 2.4 будет следовать:

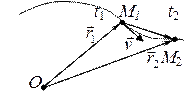Рис. 2.4 – К определению скорости точки

, . Тогда величина будет характеризовать быстроту изменения положения точки в среднем, за промежуток времени .

Переходя к пределу по времени получим в случае существования этого предела мгновенное значение скорости

. (2.4)

Таким образом, заключаем, что скорость точки есть векторная величина, определяемая как первая производная по времени от радиус-вектора точки.

В связи с тем, что предельным направлением хорды М₁М₂ будет касательная в т. М₁, то заключаем, что направление вектора скорости определяется касательной к траектории в текущем положении т. М.

Координатный способ. Представим радиус-вектор через его проекции – разложением по осям координат

.

Тогда скорость согласно определению (2.4) представится формулой

. (2.5)

Так как вектор скорости также представим разложением по осям координат

(2.6)

то из сравнения формул (2.5) и (2.6) сразу следует, что

(2.7)

Откуда получаем формулы для модуля и направляющих косинусов вектора скорости

, , .

Естественный способ. При наличии траектории линия, вдоль которой расположен вектор скорости (касательная), вполне определена. (рис. 2.5). Поэтому следует определить только алгебраическую проекцию вектора скорости на направление касательной. Поэтому

Рисунок 2.5 – Скорость точки при естественном способе

(2.8)

Ускорение точки. Определение ускорения в различных способах задания движения точки.Для характеристики быстроты изменения скорости точки введем кинематическую характеристику – ускорение точки. Определим его для всех трех видов задания движения точки.

Векторный способ.Из рис. 2.6 будет следовать:

Рис. 2.6 – К определению ускорения точки

Величина будет характеризовать быстроту изменения скорости точки в среднем, за промежуток времени .

Читайте также:  Способ утепления стен дома снаружи

Переходя к пределу по времени получим в случае существования этого предела мгновенное значение ускорения

. (2.9)

Таким образом, заключаем, что ускорение точки есть векторная величина, определяемая как первая производная по времени от вектора скорости точки.

В связи с тем, что предельным положением плоскости, образованной векторами скоростей и , является соприкасающаяся плоскость, заключаем, что вектор ускорения расположен в этой плоскости.

Координатный способ. Представим вектор скорости через его проекции – разложением по осям координат

.

Тогда ускорение согласно определению (2.9) представится формулой

. (2.10)

Так как вектор ускорения также представим разложением по осям координат

(2.11)

то из сравнения формул (2.10) и (2.11) сразу следует, что

(2.12)

Откуда получаем формулы для модуля и направляющих косинусов вектора ускорения

, , .

Естественный способ. В связи с указанным расположением векторов скорости и ускорения точки, удобно ввести систему координат, связанную с касательной к траектории и с соприкасающейся плоскостью (рис. 2.7). В этой системе координат начало располагается в движущейся точке. Первая ось – касательная τ (тангента) направляется по касательной в сторону увеличения дуговой координаты s. Вторая ось – главная нормаль n (нормаль) – перпендикулярна тангенте лежит в соприкасающейся плоскости и направлена внутрь траектории. Третья ось b – бинормаль, дополняет систему координат до правой.

Рис. 2.7. Естественная система координат и векторы скорости и ускорения точки

Из формул (2.9) и (2.8) будет следовать

.

Отсюда видно, что ускорение точки имеет две составляющие. Преобразуем второе слагаемое. Для этого с помощью рис. 2.8 вычислим производную

,

где ‑ орт главной нормали, ‑ норма орта касательной, Δφ – угол смежности – угол между двумя касательными (главными нормалями) двух соседних точек кривой, K – кривизна, ρ – радиус кривизны траектории в данной точке

Рис. 2.8. К выводу нормального ускорения

Из свойств равнобедренного треугольника ABC следует, что при Δt->0 направление вектора стремится к главной нормали, а модуль его находится по формуле . После подстановки первого замечательного предела и домножения числителя и знаменателя под пределом на Δs появляется кривизна траектории и ее радиус . Итак, мы получили

, (2.13)

где касательное (тангенциальное) ускорение , (2.14)

нормальное ускорение , (2.15)

бинормальное ускорение . (2.16)

Если скорость точки постоянна ( ), то тангенциальное ускорение равно нулю, наоборот, если траектория – прямая линия, то K=0 (ρ=∞) и нормальное ускорение равно нулю. Поэтому говорят, что физический смысл полученных составляющих в том, что

Тангенциальное (касательное) ускорение характеризует изменение
скорости по величине (по модулю), а нормальное – по направлению

Так как полученные составляющие ускорения точки взаимно перпендикулярны, то .

Вектор ускорения составляет угол с единичным вектором касательной к траектории (рис. 9). Касательное ускорение может быть записано как скалярное произведение вектора ускорения на вектор : . С другой стороны скалярное произведение вектора ускорения на вектор скорости точки имеет вид: . Сравнивая эти две формулы, получим: . Таким образом, имея проекции векторов скорости и ускорения на оси декартовой системы координат, можно вычислить касательное ускорение точки с помощью формулы:

(2.17)

Рисунок 2.9 – Определение касательного ускорения через проекции
скорости и ускорения на оси координат

Если точка движется в плоскости, то Что касается направления вектора , то если знак положительный, то направление совпадает с направлением вектора скорости точки, а если отрицательный ‑ то направление будет противоположным направлению вектора скорости точки.

Далее можно вычислить нормальное ускорение и радиус кривизны траектории: (2.18)

Таким образом, если известны уравнения движения точки, можно определить все ее кинематические характеристики в любой момент времени.

Источник