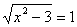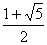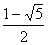Иррациональные уравнения примеры 10 класс с решением способы

Как решать иррациональные уравнения. Примеры.

Уравнения, в которых под знаком корня содержится переменная, называт иррациональными.

Методы решения иррациональных уравнений, как правило, основаны на возможности замены (с помощью некоторых преобразований) иррационального уравнения рациональным уравнением, которое либо эквивалентно исходному иррациональному уравнению, либо является его следствием. Чаще всего обе части уравнения возводят в одну и ту же степень. При этом получается уравнение, являющееся следствием исходного.

При решении иррациональных уравнений необходимо учитывать следующее:

1) если показатель корня — четное число, то подкоренное выражение должно быть неотрицательно; при этом значение корня также является неотрицательным (опредедение корня с четным показателем степени);

2) если показатель корня — нечетное число, то подкоренное выражение может быть любым действительным числом; в этом случае знак корня совпадает со знаком подкоренного выражения.

Пример 1. Решить уравнение

Возведем обе части уравнения в квадрат.
x 2 — 3 = 1;
Перенесем -3 из левой части уравнения в правую и выполним приведение подобных слагаемых.
x 2 = 4;
Полученное неполное квадратное уравнение имеет два корня -2 и 2.

Произведем проверку полученных корней, для этого произведем подстановку значений переменной x в исходное уравнение.
Проверка.
При x₁ = -2 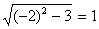— истинно:
При x₂ = -2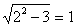— истинно.
Отсюда следует, что исходное иррациональное уравнение имеет два корня -2 и 2.

Пример 2. Решить уравнение .

Это уравнение можно решить по такой же методике как и в первом примере, но мы поступим иначе.

Найдем ОДЗ данного уравнения. Из определения квадратного корня следует, что в данном уравнении одновременно должны выполнятся два условия:

а) x — 90;

x9;

б) 1 — x0;

-x-1 ;

x1.

ОДЗ данного уранения: x.

Ответ: корней нет.

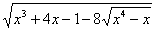
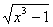
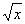
Пример 3. Решить уравнение=+ 2.

Нахождение ОДЗ в этом уравнении представляет собой достаточно трудную задачу. Возведем обе части уравнения в квадрат:
x 3 + 4x — 1 — 8= x 3 — 1 + 4+ 4x;
=0;
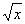
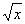
x₁=1; x₂=0.
Произведя проверку устанавливаем, что x₂=0 лишний корень.
Ответ: x₁=1.

Пример 4. Решить уравнение x =.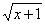

В этом примере ОДЗ найти легко. ОДЗ этого уравнения: x[-1;).

Возведем обе части этого уравнения в квадрат, в результате получим уравнение x 2 = x + 1. Корни этого уравнения:

x₁ =

x₂ =

Произвести проверку найденных корней трудно. Но, несмотря на то, что оба корня принадлежат ОДЗ утверждать, что оба корня являются корнями исходного уравнения нельзя. Это приведет к ошибке. В данном случае иррациональное уравнение равносильно совокупности двух неравенств и одного уравнения:

x + 10 и x0 и x 2 = x + 1, из которой следует, что отрицательный корень для иррационального уравнения является посторонним и его нужно отбросить.

Ответ:

Пример 5 . Решить уравнение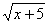+= 7.

Возведем обе части уравнения в квадрат и выполним приведение подобных членов, перенес слагаемых из одной части равенства в другую и умножение обеих частей на 0,5. В результате мы получим уравнение
= 12, (*) являющееся следствием исходного. Снова возведем обе части уравнения в квадрат. Получим уравнение (х + 5)(20 — х) = 144, являющееся следствием исходного. Полученное уравнение приводится к виду x 2 — 15x + 44 =0.

Это уравнение (также являющееся следствием исходного) имеет корни x₁ = 4, х₂ = 11. Оба корня, как показывает проверка, удовлетворяют исходному уравнению.

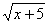
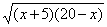
Замечание. При возведении уравнений в квадрат учащиеся нередко в уравнениях типа (*) производят перемножение подкоренных выражений, т. е. вместо уравнения•= 12, пишут уравнение = 12. Это не приводит к ошибкам, поскольку уравнения являются следствиями уравнений. Следует, однако, иметь в виду, что в общем случае такое перемножение подкоренных выражений дает неравносильные уравнения.

В рассмотренных выше примерах можно было сначала перенести один из радикалов в правую часть уравнения. Тогда в левой части уравнения останется один радикал и после возведения обеих частей уравнения в квадрат в левой части уравнения получится рациональная функция. Такой прием (уединение радикала) довольно часто применяется при решении иррациональных уравнений.

Пример 6. Решить уравнение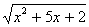—= 3.

Уединив первый радикал, получаем уравнение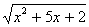
=+ 3, равносильное исходному.

Возводя обе части этого уравнения в квадрат, получаем уравнение

x 2 + 5x + 2 = x 2 — 3x + 3 + 6, равносильное уравнению

4x — 5 = 3(*). Это уравнение является следствием исходного уравнения. Возводя обе части уравнения в квадрат, приходим к уравнению
16x 2 — 40x + 25 = 9(x 2 — Зх + 3), или

7x 2 — 13x — 2 = 0.

Это уравнение является следствием уравнения (*) (а значит, и исходного уравнения) и имеет корни. Первый корень x₁ = 2 удовлетворяет исходному уравнению, а второй x₂ =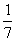— не удовлетворяет.

Заметим, что если бы мы сразу, не уединив один из радикалов, возводили обе части исходного уравнения в квадрат нам бы пришлось выполнить довольно громозкие преобразования.

При решении иррациональных уравнений, кроме уединения радикалов используют и другие методы. Рассмотрим пример использования метода замены неизвестного (метод введения вспомогательной переменной).

Пример 7. Решить уравнение 2x 2 — 6x +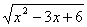+ 2 = 0.

Введем вспомогательную переменную. Пусть y =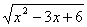, где y0, тогда получим уравнение 2y 2 + y — 10 = 0;
y₁ = 2; y₂ = —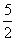. Второй корень не удовлетворяет условию y0.
Возвращаемся к x: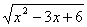
= 2;
x 2 — 3x + 6 = 4;
x 2 -3x + 2 = 0;
x₁ = 1; x₂ = 2. Проверкой устанавливаем, что оба корня являются корнями иисходного уравнения.
Ответ: x₁ = 1; x₂ = 2.

Пример 8. Решить уравнение+=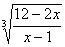

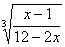
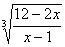
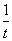
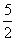
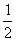
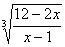
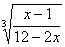
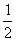
Положим= t, Тогда уравнение примет вид t +=откуда получаем следствие: 2t 2 — 5t + 2 = 0 Решая это квадратное уравнение, находим два корня: t₁ = 2 t₂ =. Задача сводится теперь к решению следующих двух уравнений:
= 2,(*)=(**)

Возводя обе части уравнения (*) в куб, получаем 12 — 2x = 8x — 8; x₁ = 2.

Аналогично, решив (**), находим x₂ =.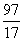

Оба найденных корня удовлетворяют исходному уравнению, так как в процессе решения мы использовали (кроме замены неизвестного) только преобразование вида [f(x) = g(x)][f n (x) = g n (x)], а при таком преобразовании, как было отмечено выше, получается равносильное уравнение.

Ответ: х₁ = 2, x₂ =.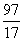

Источник

Иррациональные уравнения (ЕГЭ 2022)

Знаешь, за что, согласно легендам, убили одного древнего математика-философа по имени Гиппас?

За то, что он открыл иррациональные числа! А другие философы сочли, что такое открытие нарушает «идеальность» окружающей нас природы.

Сегодня ты узнаешь, что такое иррациональность, как решать иррациональные уравнения и почему нам не следует бояться их, как это делали древние математики!

Иррациональные уравнения — коротко о главном

Иррациональными уравнениями называются уравнения, в которых переменная содержится под знаком корня или знаком возведения в дробную степень.

Для того, чтобы решить иррациональное уравнение, необходимо:

• Уединить одно из выражений с корнем в одной части и избавиться от знака корня (возвести в соответствующую степень обе части уравнения и упростить его);
• Повторять эту процедуру, пока все корни не уйдут или пока решение не станет очевидным;
• Решить получившееся рациональное уравнение;
• Для проверки подставить получившиеся корни уравнения в исходное уравнение.

Чтобы хорошо понять, о чем здесь пойдет речь, повтори темы:

Что такое иррациональные уравнения?

Не секрет же, что большинство чисел можно представить в виде обыкновенной дроби с натуральными числами в числителе и знаменателе?

Например, число 7 – это \(\frac<21><3>\)

Иррациональные числа не такие. Их невозможно представить в виде дроби. Они странные.

Гиппас создал античным математикам множество проблем: их теории о том, что все в мире соизмеримо целым числам, рушились одна за другой. И они боялись.

Но мы будем смелыми 🙂

Сначала разберемся, что такое рациональные уравнения, а потом научимся находить решение иррациональных уравнений.

Итак, что из себя представляют рациональные уравнения, а что – иррациональные:

• \( 3\cdot (x+1)=x\) – как думаешь, какое это? Тут сложение, умножение, нет корней, и степеней никаких – рациональное!
• \( 3\cdot (x+1)=\sqrt\) – вот тебе и корень из переменной, значит уравнение НЕ рациональное (или иррациональное);
• \( 3\cdot (x+1)=\frac<1>\) – а это – рациональное;
• \( 3\cdot (x+1)=<^<2>>\) – тут вот степень, но она с целым показателем степени (\( 2\)– целое число) – значит, это тоже рациональное уравнение;
• \( 3\cdot (x+1)=<^<-1>>\) – даже уравнение с отрицательным показателем степени тоже является рациональным, ведь, по сути, \( <^<-1>>\) – это \( \frac<1>\);
• \( 3\cdot (x+1)=<^<0>>\) – тоже рациональное, т.к. \( <^<0>>=1\);
• \( 3\cdot (x+1)=<^<\frac<1><2>>>\) – а с ним поосторожнее, степень-то дробная, а по свойству корней \( <^<\frac<1><2>>>=\sqrt\), как ты помнишь, корня в рациональных уравнениях не бывает.

Надеюсь, теперь ты сможешь различить, к какому виду относится то или иное уравнение.

Иррациональными уравнениями называются уравнения, в которых переменная содержится под знаком корня или знаком возведения в дробную степень.

Но только отличать рациональное от иррационального недостаточно, тебе же решать их надо! Вся сложность в корнях, так?

Так избавься от них, вот и все дела!

Если еще не догадался, как, то я подскажу: просто возведи в нужную степень обе части уравнения, а потом решай его как простое рациональное уравнение.

Но проверяй все корни! Позже ты поймешь, почему делать это необходимо.

Как рациональные уравнения решать помнишь? Если забыл, то советую почитать «Рациональные уравнения».

Если читать лень, напомню вкратце. Для верного решения рациональных уравнений, ты должен придерживаться следующего алгоритма:

Алгоритм решения рациональных уравнений

• Понять, точно ли перед тобой рациональное уравнение (убедись, что в нем нет корней);
• Определить ОДЗ;
• Найти общий знаменатель дробей и умножить на него обе части уравнения;
• Решить получившееся целое уравнение;
• Исключить из его корней те, которые обращают в ноль знаменатель дробей.

Вроде все объяснил, давай решать, математика слов не любит.

Источник