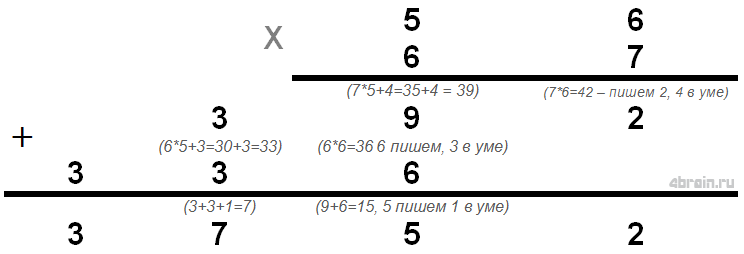Интересный способ умножения двузначных чисел

Урок 3. Традиционное умножение в уме

Давайте рассмотрим, как можно умножать двузначные числа, используя традиционные методы, которым нас обучают в школе. Некоторые из этих методов, могут позволить вам быстро перемножать в уме двузначные числа при достаточной тренировке. Знать эти методы полезно. Однако важно понимать, что это лишь вершина айсберга.

В данном уроке рассмотрены наиболее популярные приемы умножения двузначных чисел.

Первый способ – раскладка на десятки и единицы

Самым простым для понимания способом умножения двузначных чисел является тот, которому нас научили в школе. Он заключается в разбиении обоих множителей на десятки и единицы с последующим перемножением получившихся четырех чисел. Этот метод достаточно прост, но требует умения удерживать в памяти одновременно до трех чисел и при этом параллельно производить арифметические действия.

Проще такие примеры решаются в 3 действия. Сначала умножаются десятки друг на друга. Потом складываются 2 произведения единиц на десятки. Затем прибавляется произведение единиц. Схематично это можно описать так:

• Первое действие: 60*80 = 4800 — запоминаем
• Второе действие: 60*5+3*80 = 540 – запоминаем
• Третье действие: (4800+540)+3*5= 5355 – ответ

Для максимально быстрого эффекта потребуется хорошее знание таблицы умножения чисел до 10, умение складывать числа (до трехзначных), а также способность быстро переключать внимание с одного действия на другое, держа предыдущий результат в уме. Последний навык удобно тренировать путем визуализации совершаемых арифметических операций, когда вы должны представлять себе картинку вашего решения, а также промежуточные результаты.

Вывод. Не трудно убедиться в том, что этот способ не является самым эффективным, то есть позволяющим при наименьших действиях получить правильный результат. Следует принять во внимание другие способы.

Второй способ – арифметические подгонки

Приведение примера к удобному виду является достаточно распространенным способом счета в уме. Подгонять пример удобно, когда вам нужно быстро найти примерный или точный ответ. Желание подгонять примеры под определенные математические закономерности часто воспитывается на математических кафедрах в университетах или в школах в классах с математическим уклоном. Людей учат находить простые и удобные алгоритмы решения различных задач. Вот некоторые примеры подгонки:

Пример 49*49 может решаться так: (49*100)/2-49. Сначала считается 49 на сто – 4900. Затем 4900 делится на 2, что равняется 2450, затем вычитается 49. Итого 2401.

Произведение 56*92 решается так: 56*100-56*2*2*2. Получается: 56*2= 112*2=224*2=448. Из 5600 вычитаем 448, получаем 5152.

Этот способ может оказаться эффективнее предыдущего только в случае, если вы владеете устным счетом на базе перемножения двузначных чисел на однозначные и можете держать в уме одновременно несколько результатов. К тому же приходится тратить время на поиск алгоритма решения, а также уходит много внимания за правильным соблюдением этого алгоритма.

Вывод. Способ, когда вы стараетесь умножить 2 числа, раскладывая их на более простые арифметические процедуры, отлично тренирует ваши мозги, но связан с большими мысленными затратами, а риск получить неправильный результат выше, чем при первом методе.

Третий способ — мысленная визуализация умножения в столбик

56*67 – посчитаем в столбик.

Наверное, счет столбиком содержит максимальное количество действий и требует постоянно держать в уме вспомогательные числа. Но его можно упростить. Во втором уроке рассказывалось, что важно уметь быстро умножать однозначные числа на двузначные. Если вы уже умеете это делать на автомате, то счет в столбик в уме для вас будет не таким уж и трудным. Алгоритм таков

Первое действие: 56*7 = 350+42=392 – запомните и не забывайте до третьего действия.

Второе действие: 56*6=300+36=336 (ну или 392-56)

Третье действие: 336*10+392=3360+392=3 752 – тут посложнее, но вы можете начинать называть первое число, в котором уверены – «три тысячи…», а пока говорите, складывайте 360 и 392.

Вывод: счет в столбик напрямую сложен, но вы можете, при наличии навыка быстрого умножения двузначных чисел на однозначные, его упросить. Добавьте в свой арсенал и этот метод. В упрощенном виде счет в столбик является некоторой модификацией первого метода. Что лучше – вопрос на любителя.

Как можно заметить, ни один из описанных выше способов не позволяет считать в уме достаточно быстро и точно все примеры умножения двузначных чисел. Нужно понимать, что использование традиционных способов умножения для счета в уме не всегда является рациональным, то есть позволяющим при наименьших усилиях достигать максимального результата.

Источник

Без калькулятора: умножаем большие числа в уме

В эру цифровых технологий у нас пропала необходимость запоминать телефоны и адреса, считать в голове. Даже ориентироваться на местности нам помогают гаджеты. Устный счет последний раз мы применяем в школе, а зря. Помимо удобства (ведь вы можете сами быстро все посчитать, не доставая смартфон), умение быстро умножать и делить здорово тренирует мозг. А если мозг не тренировать, он ленится, что приводит к ухудшению всех его функций и нашей продуктивности. Еще до времен повсеместного распространения вычислительных машин люди изобрели несколько лайфхаков устного счета. Рассмотрим их подробнее.

Гаусс — не только распределение

Еще когда будущий «король математиков» и автор закона, названного его именем, Карл Фридрих Гаусс отличался уникальными навыками. По легенде, примерно в возрасте 3 лет он заметил, что платежные ведомости его отца рассчитаны неправильно. После проверки оказалось, что мальчик был прав. В дальнейшем он продемонстрировал феноменальные математические способности. И некоторые лайфхаки устного счета называют тоже его именем.

Достаточно одной таблицы

Чтобы научиться перемножать любые числа, нам необходимо помнить таблицу умножения. Хитрость заключается в том, что любое большое число можно разложить на маленькие — те, что представлены в этой таблице. Суть умножения двух чисел заключается в многократном повторении одного из них. Например, 7 умножить на 3 — означает, что число 7 надо повторить 3 раза: 7+7+7 = 7*3 = 21.

Если перед нами стоит задача умножить однозначное число на многозначное, то достаточно разложить больше на маленькие по разрядам, т.е. сначала сотни, потом десятки, потом единицы. И по очереди их умножить на заданное число. Далее останется сложить эти произведения. Например, 254*7 = 200*7 + 50*7 + 4*7 = 1400 + 350 + 28 = 1778. Как мы видим, каждый разряд представляет собой однозначное число с определенным количеством нулей. Таким образом, нам нужно лишь помнить таблицу умножения, чтобы легко справиться с этой задачей.

Этот же способ применим для умножения двух двузначных чисел — их нужно так же разбить на однозначные и выполнить операцию последовательно. Допустим, наша задача умножить 67 на 43. 43 — это 40 + 3. А значит, 67 нужно умножить сначала на 40, затем на 3, и сложить эти произведения. Далее раскладываем 67 и производим ту же операцию. Получаем: 67*40 + 67*3 = 60*40 + 7*40 + 60*3 + 7*3 = 2400 + 280 + 180 + 21 = 2881.

Одиннадцать друзей умножения

Самый простой и интересный способ умножения двузначного числа — с использованием числа 11. Нужно всего лишь сложить между собой цифры, из которых состоит двузначное число. А по бокам поставить те же самые исходные 2 числа, которые мы складывали. Что получится, если 35 умножить на 11? Складываем 3 + 5 = 8, а по бокам ставим 3 и 5 — 385. Проверяем на калькуляторе. Но что делать, если сумма двух этих чисел больше 10? Куда что ставить? Нужно сделать все ровно так же, только при помощи наложения. Посмотрим на примере 83*11: 8 + 3 = 11. Посередине у нас стоит 11, справа 3, а к первому месту прибавляется 8, итого: 8 + 1 = 9 — это первое число. Далее у нас стояла единица, последней тройка. Собираем: 913. Проверяем. Вуаля!

Лайфхаки не тренировка

Конечно, само слово «лайфхак» подразумевает, что мы используем определенный прием, чтобы меньше напрягать мозг. При таком счете мозг тоже тренируется — ведь нам надо удерживать всю раскладку в голове, да еще и складывать эти элементы. Чтобы быстро выучить эти методики, а также дополнительно поддерживать функции мозга в тонусе, нам нужны полноценные тренировки. Они позволят освоить еще больше лайфхаков, быстро адаптироваться в незнакомых ситуациях и не теряться при виде больших данных.

Викиум разработал более 75 специальных — когнитивных тренажеров. Они развивают базовые (когнитивные) функции мозга комплексно, по запатентованной технологии. Программа составляет вам персональный план тренировок, следит за прогрессом, постепенно повышает нагрузку. Сами тренажеры выглядят как игровые задания с понятным интерфейсом — на них могут заниматься даже дети от 7 лет. В результате регулярных тренировок существенно увеличивается работоспособность мозга и ваша общая продуктивность. Занимайтесь каждый день всего по 10 минут и будьте в тонусе!

Источник

Нетрадиционные способы умножения многозначных чисел

Краткая аннотация исследовательской работы
Каждый школьник умеет умножать многозначные числа «столбиком». В данной работе автор обращает внимание на существование альтернативных способов умножения, доступных младшим школьникам, которые могут «нудные» вычисления превратить в весёлую игру.
В работе рассматриваются шесть нетрадиционных способов умножения многозначных чисел, используемые в различные исторические эпохи: русский крестьянский, решетчатый, маленький замок, китайский, японский, по таблице В.Оконешникова.
Проект предназначен для развития познавательного интереса к изучаемому предмету, для углубления знаний в области математики.
Оглавление
Введение 3
Глава 1. Альтернативные способы умножения 4
1.1. Немного истории 4
1.2. Русский крестьянский способ умножения 4
1.3. Умножение способом «Маленький замок» 5
1.4. Умножение чисел методом «ревность» или «решётчатое умножение» 5
1.5. Китайский способ умножения 5
1.6. Японский способ умножения 6
1.7. Таблица Оконешникова 6
1.8.Умножение столбиком. 7
Глава 2. Практическая часть 7
2.1. Крестьянский способ 7
2.2. Маленький замок 7
2.3. Умножение чисел методом «ревность» или «решётчатое умножение» 7
2.4. Китайский способ 8
2.5. Японский способ 8
2.6. Таблица Оконешникова 8
2.7. Анкетирование 8
Заключение 9
Приложение 10

«Предмет математики настолько серьезен, что полезно не упускать случаев делать его немного занимательным».
Б. Паскаль
Введение
Человеку в повседневной жизни невозможно обойтись без вычислений. Поэтому на уроках математики нас в первую очередь учат выполнять действия над числами, то есть считать. Умножаем, делим, складываем и вычитаем мы привычными для всех способами, которые изучаются в школе. Возник вопрос: а есть ли еще какие-нибудь альтернативные способы вычислений? Мне захотелось изучить их более подробно. В поисках ответа на возникшие вопросы было проведено данное исследование.
Цель исследования: выявление нетрадиционных способов умножения для изучения возможности их применения.
В соответствии с поставленной целью нами были сформулированные следующие задачи:
— Найти как можно больше необычных способов умножения.
— Научиться их применять.
— Выбрать для себя самые интересные или более легкие, чем те, которые предлагаются в школе, и использовать их при счете.
— Проверить на практике умножения многозначных чисел.
— Провести анкетирование учащихся 4-х классов
Объект исследования: различные нестандартные алгоритмы умножения многозначных чисел
Предмет исследования: математическое действие «умножение»
Гипотеза: если существуют стандартные способы умножения многозначных чисел, возможно, есть и альтернативные способы.
Актуальность: распространение знаний об альтернативных способах умножения.
Практическая значимость. В ходе работы было решено множество примеров и создан альбом, в который включены примеры с различными алгоритмами умножениями многозначных чисел несколькими альтернативными способами. Это может заинтересовать одноклассников для расширения математического кругозора и послужит началом новых экспериментов.

Источник

Как быстро научиться умножать в уме двузначные числа?

В эпоху калькуляторов мы стали все реже производить вычислительные операции в уме. Между тем, такие упражнения отлично развивают мышление и тренируют память. Как правильно начать умножать в уме многозначные числа, чтобы эту методику понял и взрослый и ребенок? Попробуем разобраться вместе!

Способы умножения чисел в уме существуют не один десяток лет. Выберите тот, который подходит вам наиболее всего!

Разложение чисел

Считается наиболее простым способом. Большие числа нужно разложить на тысячи, сотни, десятки и единицы и перемножить разряды между собой. Попробуем перемножить 38 и 57.

• Сначала разложим числа на десятки и единицы. В первом случае это будет 30+8
• Во втором 50+7
• Умножаем десятки: 30х50=1500. Полученный результат необходимо запомнить.
• Дальше умножаем десятки на единицы того же числа. Вот так: 30х7+8=210+400=610
• Полученный результат снова запоминаем.
• Дальше вспоминаем первый полученный результат: 1500. Плюсуем к нему второй полученный результат 1500 + 610 = 2110
• Мы почти закончили! Теперь нам остается перемножить единицы (8х7=56) И полученный результат прибавляем к полученной ранее, сумме
• 2110 + 56 = 2166

Как запомнить промежуточные результаты? Первое время, возможно, придется записывать их. Но уже через пару дней вам будет достаточно простого проговаривания вслух. После нескольких недель тренировок ваш мозг будет отлично справляться с такими задачами, и умножение не только двузначных, но и более сложных чисел, будет даваться вам легко.

Источник

Эффективный счёт в уме или разминка для мозга

Эта статья навеяна топиком «Как и насколько быстро вы считаете в уме на элементарном уровне?» и призвана распространить приёмы С.А. Рачинского для устного счёта.
Рачинский был замечательным педагогом, преподававшим в сельских школах в XIX веке и показавшим на собственном опыте, что развить навык быстрого устного счёта можно. Для его учеников не было особой проблемой посчитать подобный пример в уме:

Используем круглые числа

Один из самых распространённых приёмов устного счёта заключается в том, что любое число можно представить в виде суммы или разности чисел, одно или несколько из которых «круглое»:

Т.к. на 10, 100, 1000 и др. круглые числа умножать быстрее, в уме нужно сводить всё к таким простым операциям, как 18 x 100 или 36 x 10. Соответственно, и складывать легче, «отщепляя» круглое число, а затем добавляя «хвостик»: 1800 + 200 + 190.
Еще пример:

Упростим умножение делением

При устном счёте бывает удобнее оперировать делимым и делителем нежели целым числом (например, 5 представлять в виде 10:2, а 50 в виде 100:2):

Аналогично выполняется умножение или деление на 25, ведь 25 = 100:4. Например,

Теперь не кажется невозможным умножить в уме 625 на 53:

Возведение в квадрат двузначного числа

Оказывается, чтобы просто возвести любое двузначное число в квадрат, достаточно запомнить квадраты всех чисел от 1 до 25. Благо, квадраты до 10 мы уже знаем из таблицы умножения. Остальные квадраты можно посмотреть в нижеприведённой таблице:

Приём Рачинского заключается в следующем. Для того чтобы найти квадрат любого двузначного числа, надо разность между этим числом и 25 умножить на 100 и к получившемуся произведению прибавить квадрат дополнения данного числа до 50 или квадрат избытка его над 50-ю. Например,

В общем случае (M — двузначное число):

Попробуем применить данный трюк при возведении в квадрат трёхзначного числа, разбив его предварительно на более мелкие слагаемые:

Хм, я бы не сказала, что это сильно легче, чем возведение в столбик, но, возможно, со временем можно приноровиться.
И начинать тренировки, конечно, следует с возведения в квадрат двузначных чисел, а там уже и до дизассемблирования в уме можно дойти.

Умножение двузначных чисел

Этот интересный приём был придуман 12-летним учеником Рачинского и является одним из вариантов добавления до круглого числа.
Пусть даны два двузначных числа, у которых сумма единиц равна 10:

Составив их произведение, получим:

Например, вычислим 77 x 13. Сумма единиц этих чисел равна 10, т.к. 7 + 3 = 10. Сначала ставим меньшее число перед большим: 77 x 13 = 13 x 77.
Чтобы получить круглые числа, мы забираем три единицы от 13 и добавляем их к 77. Теперь перемножим новые числа 80 x 10, а к полученному результату прибавим произведение отобранных 3 единиц на разность старого числа 77 и нового числа 10:

У этого приёма есть частный случай: всё значительно упрощается, когда у двух сомножителей одинаковое число десятков. В этом случае число десятков умножается на следующее за ним число и к полученному результату приписывается произведение единиц этих чисел. Посмотрим, как элегантен этот приём на примере.
48 x 42. Число десятков 4, последующее число: 5; 4 x 5 = 20. Произведение единиц: 8 x 2 = 16. Значит,
99 x 91. Число десятков: 9, последующее число: 10; 9 x 10 = 90. Произведение единиц: 9 x 1 = 09. Значит,
Ага, то есть, чтобы перемножить 95 x 95, достаточно посчитать 9 x 10 = 90 и 5 x 5 = 25 и ответ готов:

Тогда предыдущий пример можно вычислить немного проще:

Вместо заключения

Казалось бы, зачем уметь считать в уме в 21 веке, когда можно просто подать голосовую команду смартфону? Но если задуматься, что будет с человечеством, если оно будет взваливать на машины не только физическую работу, но и любую умственную? Не деградирует ли оно? Даже если не рассматривать устный счёт как самоцель, для закалки ума он вполне подходит.

Использованная литература:
«1001 задача для умственного счёта в школе С.А. Рачинского».

Источник