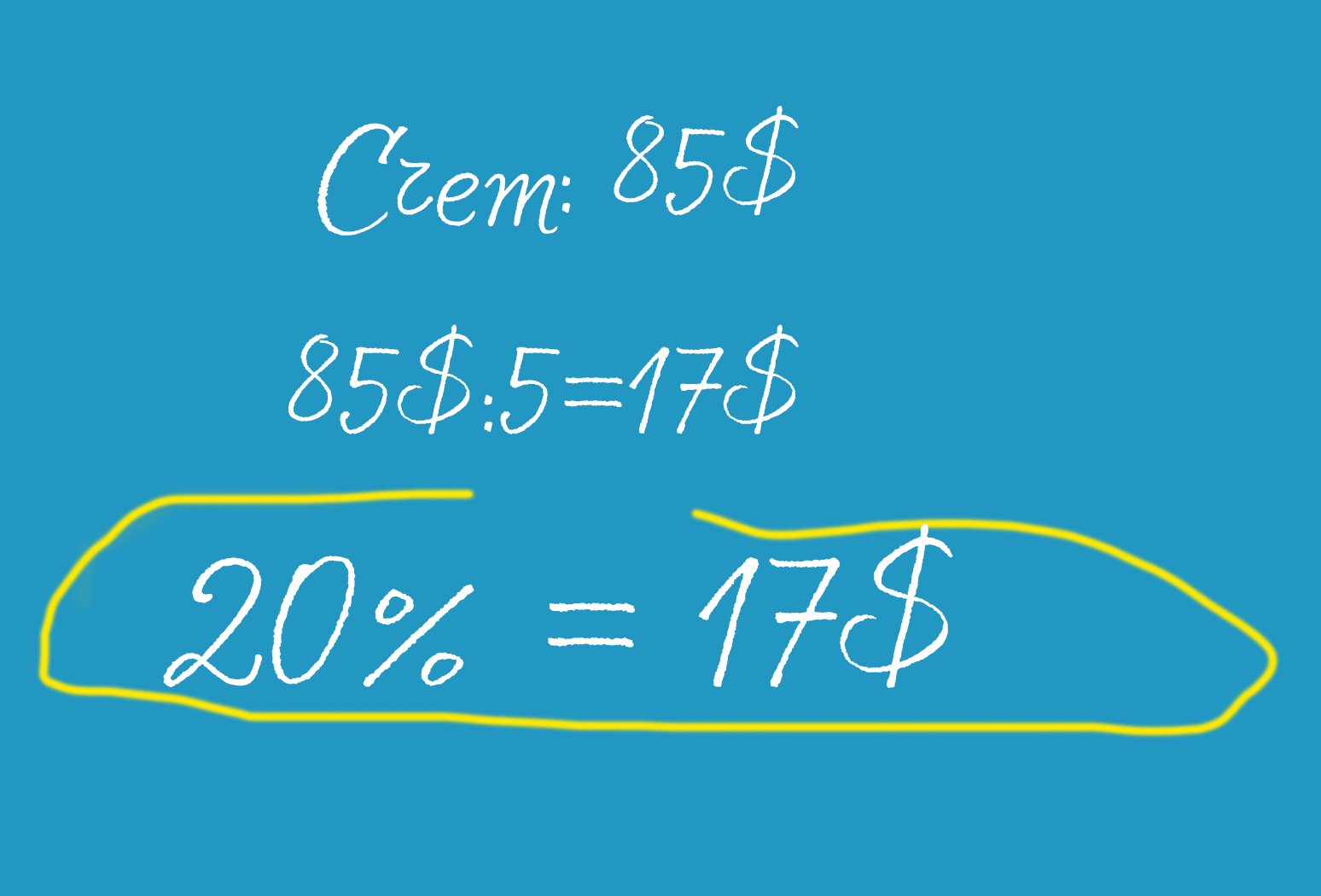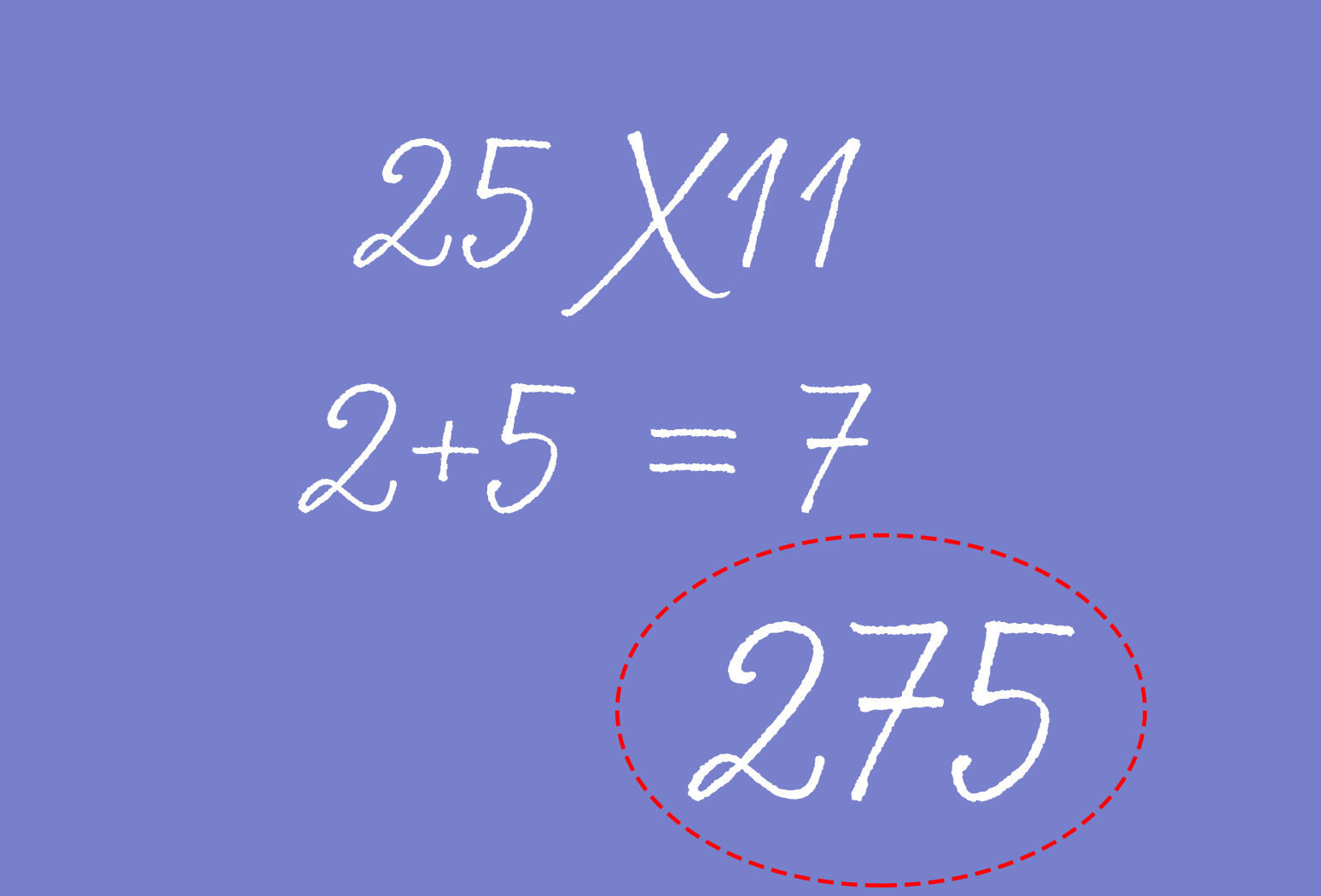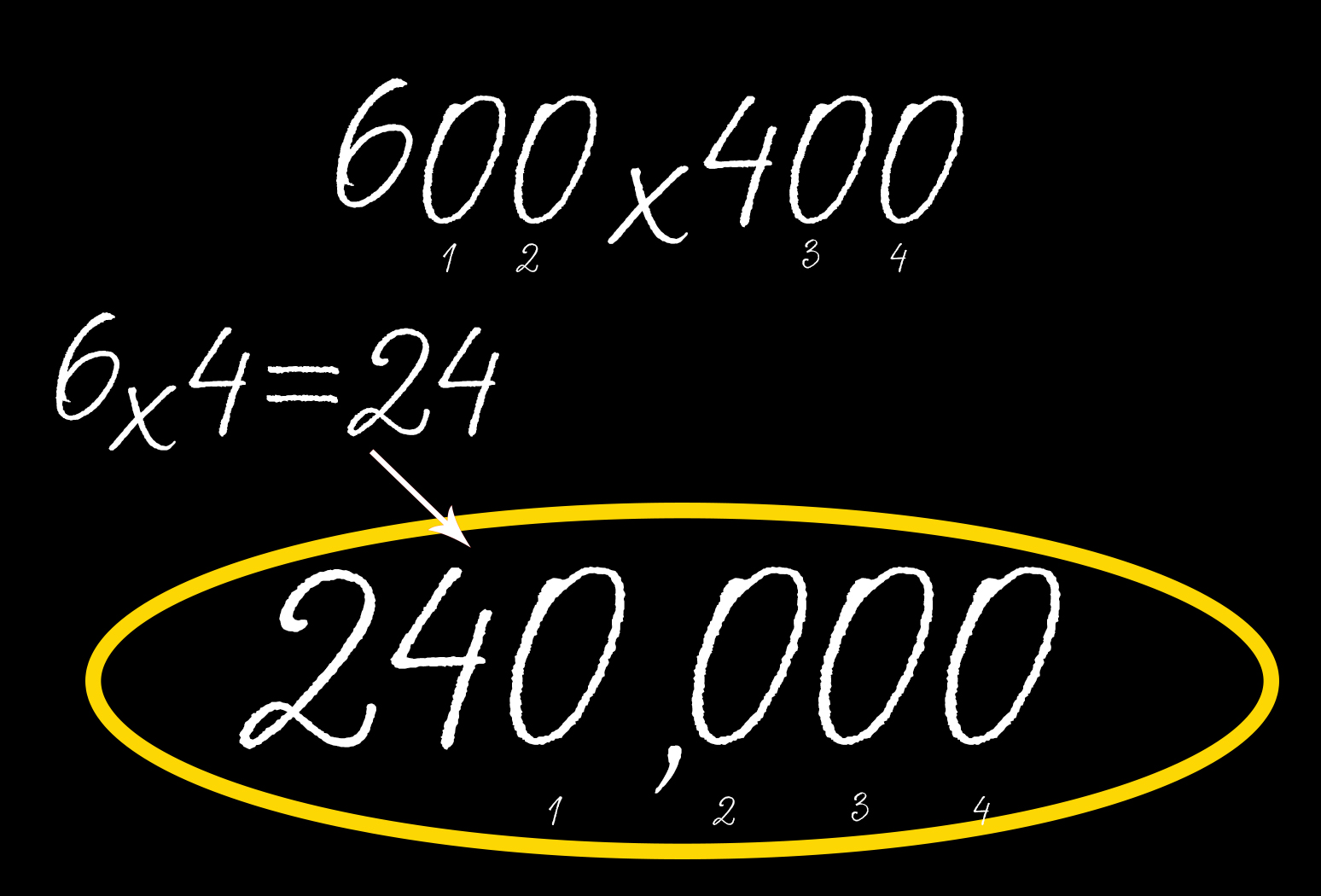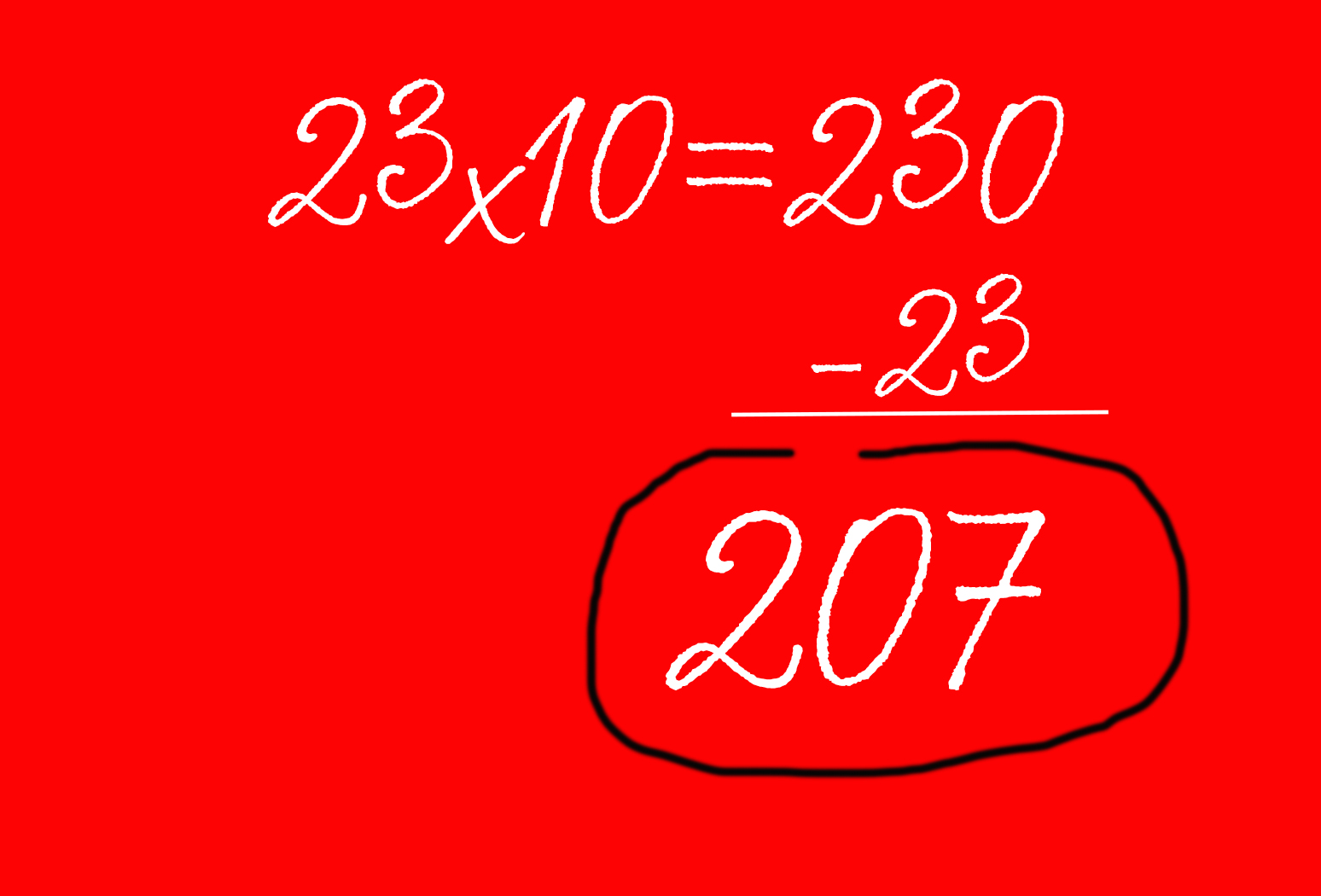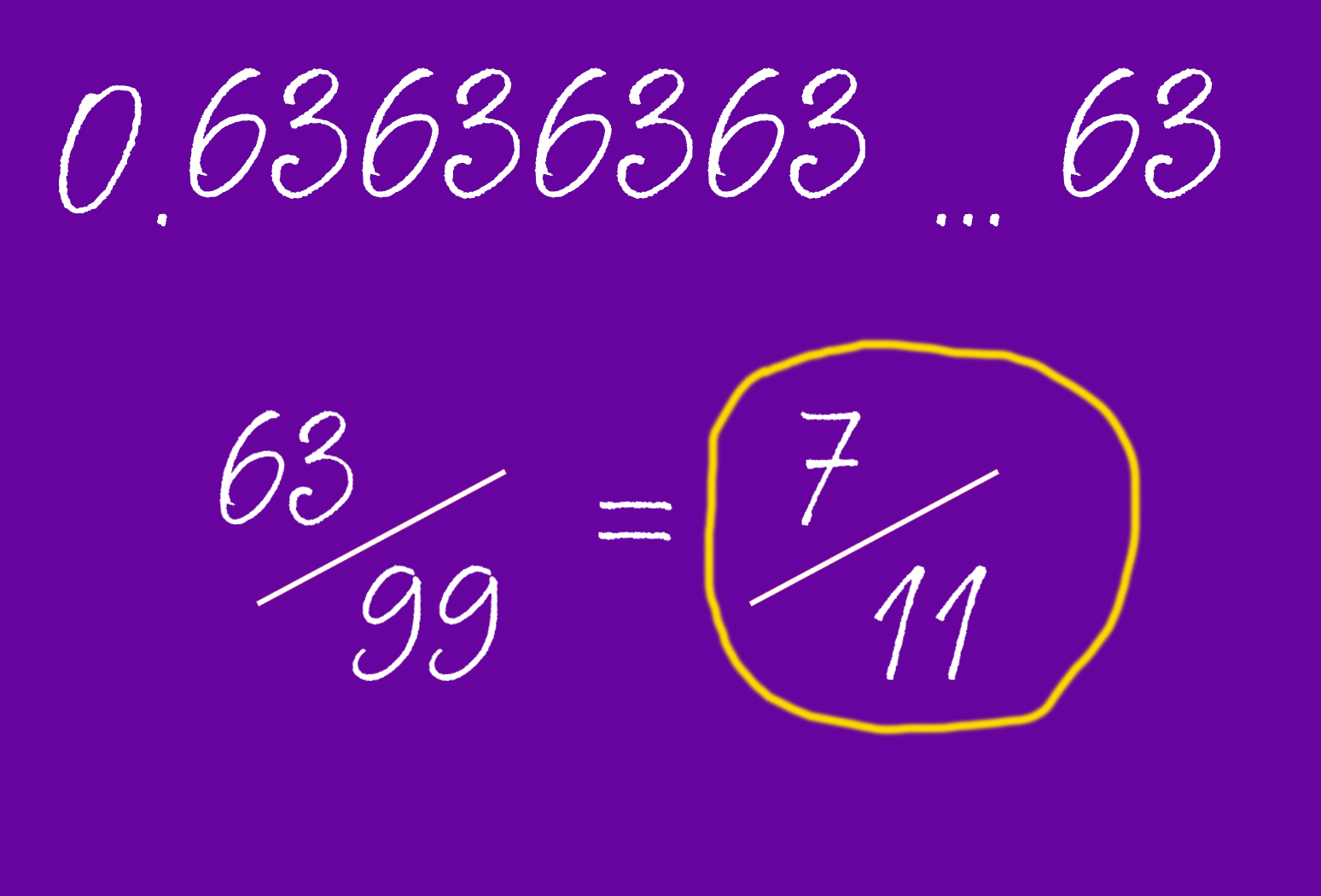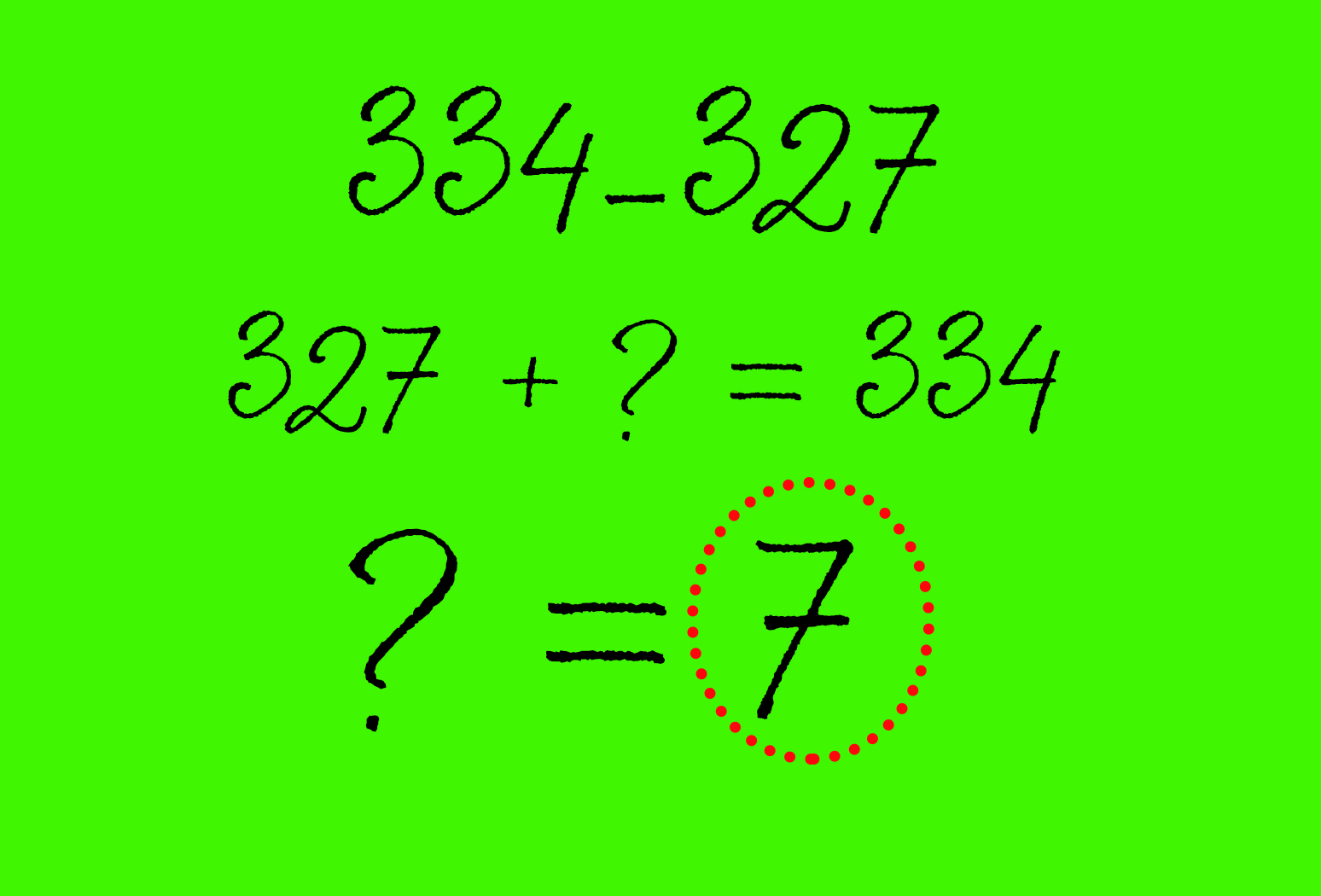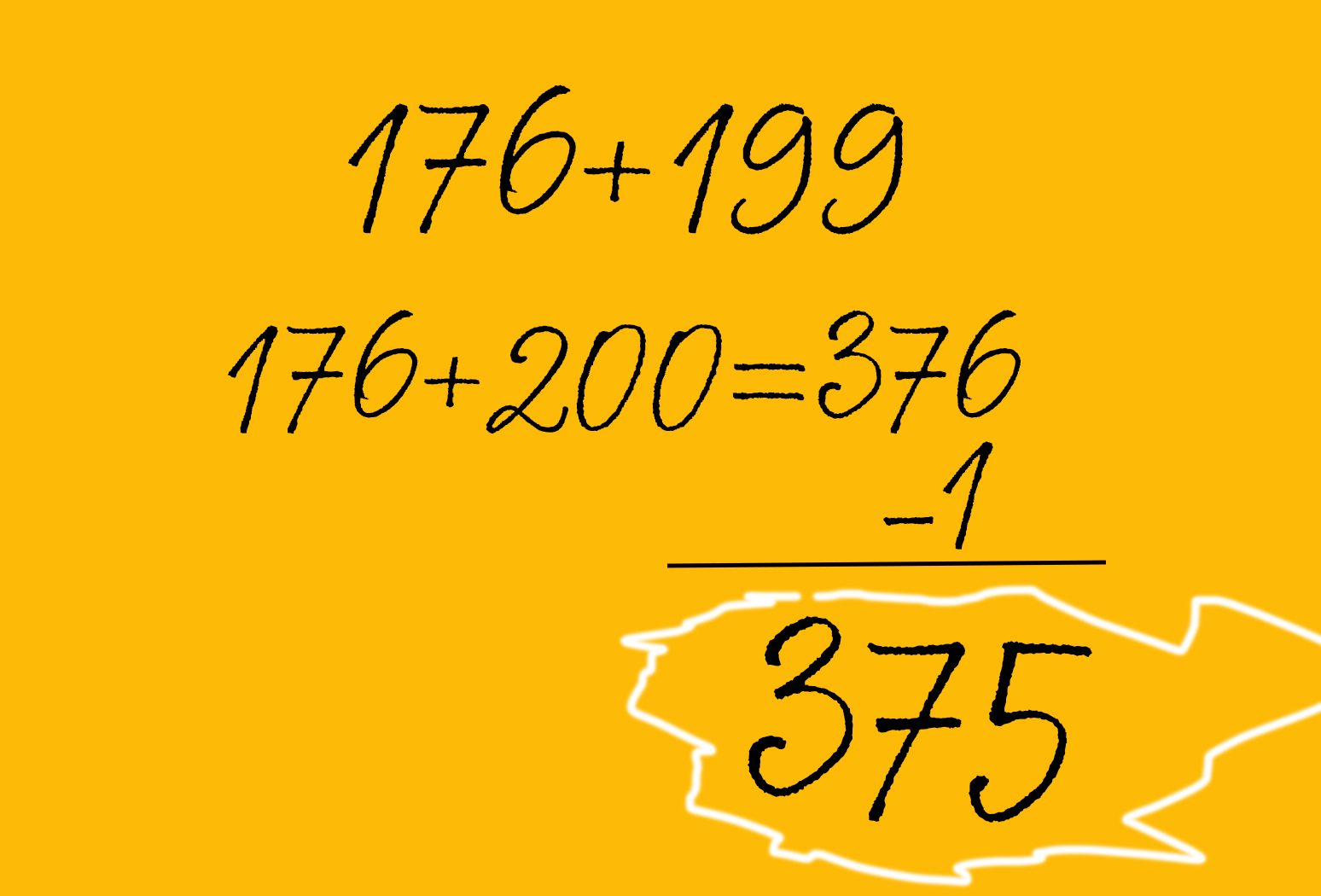Интересные способы вычисления математика

Долой калькулятор: 12 простых трюков, которые помогут вам быстро считать

Просто, как дважды два.

Как бы мы ни хотели это признавать, учителя были правы: математика нужна каждому из нас. Но далеко не всем дается ловкое жонглирование числами. Тогда на помощь приходят легко запоминающиеся математические приемы – настоящее спасение, когда под рукой, как назло, нет калькулятора.

Ниже вы найдете 12 способов быстрых вычислений для всех, кто далек от точных наук.

1. Быстрое вычисление 20%

Представим, что границы вновь открыли и первым делом вы отправились в США. А там принято оставлять на чай. Обычно размер чаевых составляет 15-20% от суммы вашего заказа.

По словам Кейт Сноу, автора серии книг The Math Facts That Stick, чтобы быстро вычислить 20% от суммы, вам нужно просто разделить число в чеке на 5.

Например, вы поели на 85 долларов. Разделите 85 на 5, и у вас получится 17 долларов – чаевые, которые вы должны оставить официанту.

2. Умножение двузначных чисел на 11

Умножить число на 11 очень легко с помощью хитрого трюка от math.hmc.edu. Просто сложите две цифры и поместите полученную сумму в середину числа.

Например, вы умножаете 25 на 11. Если сложить 2 и 5, получится 7. Теперь расположите 7 между 2 и 5, чтобы найти окончательный ответ – 275.

3. Быстрое удвоение

Чтобы удвоить большое число, умножьте каждую цифру на 2 и сложите их между собой. Кейт Сноу предлагает начинать слева – так будет легче.

«Чтобы удвоить, к примеру, 147, начните с разряда сотен. Если умножить 100 на 2, получится 200. 40 на 2 – 80. 7 на 2 – 14. Теперь сложите числа между собой (200 + 80 + 14), и вы получите 294», – объясняет Сноу.

4. Умножение чисел, которые оканчиваются на ноль

Примеры с большими пугающими числами, которые оканчиваются на ноль, тоже легко решить с помощью специального приема. Согласно education.cu-portland.edu, нужно просто «вычеркнуть» нули из примера, а в конце вновь их добавить.

Если вы умножаете 600 на 400, уберите все нули и перемножьте 6 на 4. Получится 24. Затем подсчитайте общее количество нулей в исходном уравнении и припишите их к полученному значению. Так как в нашем примере было четыре нуля, то ответ будет равен 240000.

5. Умножение на 9

Если вам так и не удалось выучить таблицу умножения – не переживайте. По словам Сноу, чтобы легко умножить число на 9, нужно умножить его на 10 и вычесть исходное число из полученного значения.

Например, вам нужно умножить 9 на 23. Для этого умножаем 23 на 10 и получаем 230. А затем вычитаем из него 23, чтобы получить окончательный ответ – 207.

6. Деление на 10, 100 или 1000

Разделить число на 10 проще простого – согласно Сноу, «нужно просто переместить десятичный знак на одну позицию влево от исходного числа, чтобы найти ответ».

Для деления на 100 применим тот же метод, за исключением одного – нужно переместить десятичный разряд на две позиции левее исходного числа. Что касается деления на 1000, просто переместите десятичный знак на три позиции влево.

Например, если вы делите 42,94 на 10, вы просто перемещаете десятичный знак на одну позицию влево и получаете 4,294.

7. Умножение на 10, 100 или 1000

Здесь все работает с точностью до наоборот. Чтобы умножить число на 10, переместите десятичный знак на одну позицию вправо. На 100 – на две позиции. На 1000 – на три позиции.

Например, если вам нужно умножить 366,78 на 100, передвиньте десятичный знак на две цифры вправо, чтобы получить ответ 36678.

8. Преобразование периодической десятичной дроби в обыкновенную

Согласно businessinsider.com, нужно выполнить всего 3 шага, чтобы легко превратить бесконечную десятичную дробь в обыкновенную, с числителем и знаменателем.

• Шаг 1. Найдите повторяющиеся цифру или число. Например, у 0,636363 это будет 63.
• Шаг 2. Определите, сколько разрядов в этом числе. В нашем случае у 63 – два разряда.
• Шаг 3. Разделите повторяющееся число на число с таким же количеством разрядов, которое будет состоять из одних девяток – в данном случае 99. Получим 63/99. Теперь сократим ее и получим 7/11 – наш ответ.

9. Умножение на 25

Умножать на 25 не так уж и сложно, если представлять число в виде дроби 100/4. В этом случае все, что вам нужно сделать, это разделить число на 4 и умножить на 100.

Например, вам нужно умножить 84 на 25. Сначала делим 84 на 4 – получаем 21, а потом умножаем значение выражения на 100. Ответ: 2100.

10. Возведение чисел, оканчивающихся на 5, в квадрат

«Этот математический трюк подразумевает 2 шага», – объясняет Сноу. Чтобы возвести в квадрат число, которое оканчивается на пять, возьмите первую цифру числа и умножьте ее на себя. После этого прибавьте к полученному результату первую цифру и припишите к ответу 25. Кружится голова? Разберем на примере.

Если вы умножаете 35 на 35, сначала умножьте 3 на 3 – получится 9, – и прибавьте 3 к ответу – получится 12. Теперь припишите 25 в конец найденного числа, и вы найдете окончательный ответ: 1225.

11. Вычитание путем сложения

Если вам кажется, что сложение немного проще, чем вычитание, этот трюк для вас. Когда вам нужно найти разность двух чисел, достаточно близких друг к другу, попробуйте решить пример с помощью сложения.

«Вместо того чтобы пытаться вычесть 327 из 334, представьте это в виде суммы: мол, сколько нужно добавить к 327, чтобы получить 334?» – объясняет Сноу.

12. Сложение чисел, оканчивающихся на 99

Если вы пытаетесь прикинуть, во сколько обойдутся продукты, стоимость которых заканчивается на 99, – калькулятор не нужен. Все, что необходимо сделать, – прибавить 100 вместо 99, а потом вычесть единицу.

Сноу объясняет этот процесс на примере 176 + 199 = 375. «Если к 176 мы прибавим 200, то получим 376, – говорит эксперт. – Поскольку вы добавили на единицу больше, чем вам нужно, вычтите ее из 376, чтобы найти правильный ответ: 375».

Источник

Интересные способы быстрого счета

Дата публикации: 20.12.2016 2016-12-20

Статья просмотрена: 16360 раз

Библиографическое описание:

Владимиров, А. И. Интересные способы быстрого счета / А. И. Владимиров, В. В. Михайлова, С. П. Шмелева. — Текст : непосредственный // Юный ученый. — 2016. — № 6.1 (9.1). — С. 15-17. — URL: https://moluch.ru/young/archive/9/633/ (дата обращения: 18.11.2021).

Введение

Устный счет – гимнастика для ума. Счет в уме является самым древним способом вычисления. Освоение вычислительных навыков развивает память и помогает усваивать предметы естественно-математического цикла.

Существует много приемов упрощения арифметических действий. Знание упрощенных приемов вычисления особенно важно в тех случаях, когда вычисляющий не имеет в своем распоряжении таблиц и калькулятора.

Мы хотим остановиться на способах сложения, вычитания, умножения, деления, для производства которых достаточно устного счета или применения ручки и бумаги.

Мотивацией для выбора темы послужило желание продолжения формирования вычислительных навыков, умения быстро и чётко находить результат математических действий.

Правила и приёмы вычислений не зависят от того, выполняются они письменно или устно. Однако владение навыками устных вычислений представляет большую ценность не потому, что в быту ими пользуются чаще, чем письменными выкладками. Это важно ещё и потому, что они ускоряют письменные вычисления, приобретают опыт рациональных вычислений, дают выигрыш в вычислительной работе.

На уроках математики приходится, много делать устных вычислений и когда учитель показал нам приём быстрого умножения на числа 11, у нас возникла идея, а существуют ли ещё приёмы быстрого вычисления. Мы поставили перед собой задачу, найти и опробовать другие приёмы быстрого вычисления.

Немногие умеют считать быстро и правильно. Исследование, проведенное в нашей школе, показало:

1. Зачем нужно уметь считать?

а) пригодится в жизни, например, считать деньги;(16%)

б) чтобы хорошо учиться в школе; (16%)

в) чтобы быстро решать; (16%)

г) чтобы быть грамотным; (52%)

д) не обязательно уметь считать.

2. Перечислите, при изучении, каких школьных предметов тебе понадобится правильно считать?

а) математика; (80%)

3. Знаешь ли ты приемы быстрого счета?

б) да, несколько (85%);

в) нет, не знаю(15%).

4. Применяешь ли ты при вычислениях приемы быстрого счета?

5. Хотели бы вы узнать приемы быстрого счета, чтобы быстро считать?

Говорят, если хотите научиться плавать, вы должны войти в воду, а если хотите уметь решать задачи, то должны начать их решать. Но для начала надо освоить азы арифметики. Научиться считать быстро, считать в уме можно только при большом желании и систематической тренировке в решении задач.

А ведь приёмы быстрого устного счёта известны давно. Великолепные способности к устному счёту таких блестящих математиков, как Гаусс, фон Нейман, Эйлер или Валлис, вызывают настоящий восторг. Об этом много написано. Мы хотим рассказать и показать некоторые известные вычислительные секреты. И тогда перед вами откроется совсем другая математика. Живая, полезная и понятная.

1.Способы быстрого умножения

1. СЧЁТ НА ПАЛЬЦАХ

Способ быстрого умножения чисел в пределах первого десятка на 9.

Допустим, нам нужно умножить 7 на 9.

Повернём руки ладонями к себе и загнём седьмой палец (начиная считать от большого пальца слева).

Число пальцев слева от загнутого будет равно десяткам, а справа – единицам искомого произведения.

Рис. 1. Счёт на пальцах

2. УМНОЖЕНИЕ ЧИСЕЛ ОТ 10 ДО 20

Можно очень просто умножать такие числа.

К одному из чисел надо прибавить количество единиц другого, умножить на 10 и прибавить произведение единиц чисел.

Пример 1. 16∙18=(16+8) ∙ 10+6 ∙ 8=288, или

Пример 2. 17 ∙ 17=(17+7) ∙ 10+7 ∙ 7=289.

Задание: Умножьте быстро 19 ∙ 13. Ответ 19 ∙13=(19+3) ∙10 +9 ∙3=247.

3. УМНОЖЕНИЕ НА 11

— Чтобы двузначное число, сумма цифр которого не превышает 10, умножить на 11, надо цифры этого числа раздвинуть и поставить между ними сумму этих цифр.

72 ∙ 11 = 7 (7 + 2) 2 = 792;

35 ∙ 11 = 3 (3 + 5) 5 = 385.

— Чтобы умножить на 11 двузначное число, сумма цифр которого 10 или больше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить единицу, а вторую и последнюю (третью) оставить без изменения.

94 ∙ 11 = 9 (9 + 4) 4 = 9 (13) 4 = (9 + 1) 34 = 1034.

Задание: Умножьте быстро 54 ∙ 11 (594)

Задание: Умножьте быстро 67∙ 11 (737)

4. УМНОЖЕНИЕ НА 22, 33, . 99

— Чтобы двузначное число умножить на 22, 33, . 99, надо этот множитель представить в виде произведения однозначного числа (от 2 до 9) на 11, то есть 44 = 4 11; 55 = 5 ∙ 11 и т.д. Затем произведение первых чисел умножить на 11.

Пример 1. 24 ∙ 22 = 24 ∙ 2 ∙ 11 = 48 ∙ 11 = 528

Пример 2. 23 ∙ 33 = 23 ∙ 3 ∙ 11= 69 ∙ 11 = 759

Задание: Умножьте 18∙ 44

5. УМНОЖЕНИЕ НА 5, НА 50, НА 25, НА 125

При умножении на эти числа можно воспользоваться следующими выражениями:

a ∙ 5=a ∙ 10:2 a ∙ 50=a ∙ 100:2

a ∙ 25=a ∙ 100:4 а ∙ 125=а ∙ 1000:8

Пример1. 17 ∙ 5=17 ∙ 10:2=170:2=85

Пример 2. 43 ∙ 50=43 ∙ 100:2=4300:2=2150

Пример 3. 27 ∙ 25=27 ∙ 100:4=2700:4=675

Пример 4. 96 ∙ 125=96:8 ∙ 1000=12 ∙ 1000=12000

Задание: умножьте 824∙25

Задание: умножьте 348∙50

&2. Способы быстрого деления

1. ДЕЛЕНИЕ НА 5, НА 50, НА 25

При делении на 5, на 50, на 25 можно воспользоваться следующими выражениями:

a:5= a ∙ 2:10 a:50=a ∙ 2:100

&3. Способы быстрого сложения и вычитания натуральных чисел.

— Если одно из слагаемых увеличить на несколько единиц, то из полученной суммы надо вычесть столько же единиц.

Пример. 785+963=785+(963+7)-7=785+970-7= 1748

— Если одно из слагаемых увеличить на несколько единиц, а второе уменьшить на столько же единиц, то сумма не изменится.

Пример. 762+639=(762+8)+(639-8)=770 + 631=1401

— Если вычитаемое уменьшить на несколько единиц и уменьшаемое увеличить на столько же единиц, то разность не изменится.

Заключение

Существуют способы быстрого сложения, вычитания, умножения, деления, возведения в степень. Мы рассмотрели лишь немногие способы быстрого счета.

Все рассмотренные нами методы устного вычисления говорят о многолетнем интересе ученых и простых людей к игре с цифрами. Используя некоторые из этих методов на уроках или дома можно развить скорость вычислений, добиться успехов в изучении всех школьных предметов.

Умножение без калькулятора – тренировка памяти и математического мышления. Вычислительная техника совершенствуется и по сей день, но любая машина делает то, что в нее закладывают люди, а мы узнали некоторые приемы устного счета, которые помогут нам в жизни.

Нам было интересно работать над проектом. Пока мы только изучали и анализировали уже известные способы быстрого счета.

Но кто знает, возможно, в будущем мы сами сможем открыть новые способы быстрых вычислений.

1. Арутюнян Е., Левитас Г. Занимательная математика.- М.: АСТ – ПРЕСС, 1999. – 368 с.
2. Гарднер М. Математические чудеса и тайны. – М., 1978.
3. Глейзер Г.И. История математики в школе. – М.,1981.
4. «Первое сентября» Математика №3(15), 2007.
5. Татарченко Т.Д. Способы быстрого счета на занятиях кружка, «Математика в школе», 2008, №7, стр.68.
6. Устный счет / Сост. П.М.Камаев. – М.: Чистые пруды, 2007- Библиотечка «Первого сентября», серия «Математика». Вып. 3(15).
7. http://portfolio.1september.ru/subject.php

Похожие статьи

Изучение приемов быстрого счета будущими учителями.

Умножение двузначных чисел, сумма единиц которых равна 10.

проектная деятельность, рациональные вычисления, приемы быстрого счета

Выполняя подобное задание, учащиеся отрабатывают прием сложения двузначных чисел без перехода и с переходом через разряд.

Приёмы быстрого счета | Статья в журнале «Юный ученый»

Приёмы быстрого счета. Рубрика: Математика: алгебра и начала анализа, геометрия.

Самым быстрым способом вычислить процент от числа является, умножение данного процента на это число с последующим отбрасыванием двух последних цифр в получившемся результате

Использование схематической модели числа при формировании.

Уметь быстро, точно, правильно выполнять вычисления необходимо уже в начальной школе

Но для того чтобы научиться правильно считать, быстро выполнять простейшие

Выполняя подобное задание, учащиеся отрабатывают прием сложения двузначных чисел без.

И снова о ментальной арифметике | Статья в журнале.

Устный счет – гимнастика для ума. Счет в уме является самым древним способом вычисления. Способ быстрого умножения чисел в пределах первого

Основные термины (генерируются автоматически): число, устный счет, проектная деятельность, двузначное число, прием.

B помощь арифметике | Статья в журнале «Молодой ученый»

Применение таких интересных методов вычисления поможет ученикам быстро осваивать основы математики.

. число b только в том случае, если сумма произведений цифр числа а на соответствующие остатки, получаемые при делении разрядных единиц на число b.

Технология «Ментальная арифметика» в организации.

Дальнейшие вычисления будут сопровождаться передвижением косточек по разрядам.

Дети быстро «схватывают» принципы быстрого счета, а также, что одно число можно составить

ментальная арифметика, устный счет, ребенок, таблица умножения, ментальный счет, число.

О применении устного счета на уроках математики

Математика является одной из важнейших наук на земле и именно с ней человек встречается каждый день. Счет в уме является самым древним и простым способом вычисления. Знание упрощенных приемов устных вычислений остается необходимым даже при полной.

Конструируя – обучаемся. Сложение и вычитание натуральных.

Сложение однозначных чисел. Число – это количественная характеристика объекта.

Разряды десятков и единиц – обнуляются. Обнуление единиц младшего разряда является окончанием выполнения задания.

&3. Способы быстрого сложения и вычитания натуральных чисел.

Методы и приемы стимулирования мышления на уроках.

Интересные способы быстрого счета. — Если вычитаемое уменьшить на несколько единиц и уменьшаемое увеличить на столько же единиц, то

Существуют способы быстрого сложения, вычитания, умножения, деления, возведения в степень. Ликвидация пробелов в знаниях при.

Похожие статьи

Изучение приемов быстрого счета будущими учителями.

Умножение двузначных чисел, сумма единиц которых равна 10.

проектная деятельность, рациональные вычисления, приемы быстрого счета

Выполняя подобное задание, учащиеся отрабатывают прием сложения двузначных чисел без перехода и с переходом через разряд.

Приёмы быстрого счета | Статья в журнале «Юный ученый»

Приёмы быстрого счета. Рубрика: Математика: алгебра и начала анализа, геометрия.

Самым быстрым способом вычислить процент от числа является, умножение данного процента на это число с последующим отбрасыванием двух последних цифр в получившемся результате

Использование схематической модели числа при формировании.

Уметь быстро, точно, правильно выполнять вычисления необходимо уже в начальной школе

Но для того чтобы научиться правильно считать, быстро выполнять простейшие

Выполняя подобное задание, учащиеся отрабатывают прием сложения двузначных чисел без.

И снова о ментальной арифметике | Статья в журнале.

Устный счет – гимнастика для ума. Счет в уме является самым древним способом вычисления. Способ быстрого умножения чисел в пределах первого

Основные термины (генерируются автоматически): число, устный счет, проектная деятельность, двузначное число, прием.

B помощь арифметике | Статья в журнале «Молодой ученый»

Применение таких интересных методов вычисления поможет ученикам быстро осваивать основы математики.

. число b только в том случае, если сумма произведений цифр числа а на соответствующие остатки, получаемые при делении разрядных единиц на число b.

Технология «Ментальная арифметика» в организации.

Дальнейшие вычисления будут сопровождаться передвижением косточек по разрядам.

Дети быстро «схватывают» принципы быстрого счета, а также, что одно число можно составить

ментальная арифметика, устный счет, ребенок, таблица умножения, ментальный счет, число.

О применении устного счета на уроках математики

Математика является одной из важнейших наук на земле и именно с ней человек встречается каждый день. Счет в уме является самым древним и простым способом вычисления. Знание упрощенных приемов устных вычислений остается необходимым даже при полной.

Конструируя – обучаемся. Сложение и вычитание натуральных.

Сложение однозначных чисел. Число – это количественная характеристика объекта.

Разряды десятков и единиц – обнуляются. Обнуление единиц младшего разряда является окончанием выполнения задания.

&3. Способы быстрого сложения и вычитания натуральных чисел.

Методы и приемы стимулирования мышления на уроках.

Интересные способы быстрого счета. — Если вычитаемое уменьшить на несколько единиц и уменьшаемое увеличить на столько же единиц, то

Существуют способы быстрого сложения, вычитания, умножения, деления, возведения в степень. Ликвидация пробелов в знаниях при.

Источник