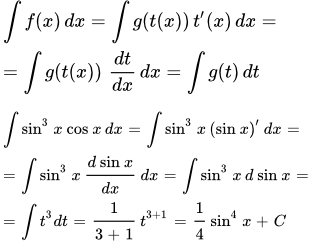Интегрирование способом подстановки метод замены переменной

Интегрирование методом замены переменной

Метод замены переменной

С помощью замены переменной можно вычислить простые интегралы и, в некоторых случаях, упростить вычисление более сложных.

Метод замены переменной заключается в том, что мы от исходной переменной интегрирования, пусть это будет x , переходим к другой переменной, которую обозначим как t . При этом мы считаем, что переменные x и t связаны некоторым соотношением x = x ( t ) , или t = t ( x ) . Например, x = ln t , x = sin t , t = 2 x + 1 , и т.п. Нашей задачей является подобрать такую зависимость между x и t , чтобы исходный интеграл либо свелся к табличному, либо стал более простым.

Основная формула замены переменной

Рассмотрим выражение, которое стоит под знаком интеграла. Оно состоит из произведения подынтегральной функции, которую мы обозначим как f ( x ) и дифференциала dx : . Пусть мы переходим к новой переменной t , выбрав некоторое соотношение x = x ( t ) . Тогда мы должны выразить функцию f ( x ) и дифференциал dx через переменную t .

Чтобы выразить подынтегральную функцию f ( x ) через переменную t , нужно просто подставить вместо переменной x выбранное соотношение x = x ( t ) .

Преобразование дифференциала выполняется так:
.
То есть дифференциал dx равен произведению производной x по t на дифференциал dt .

На практике, чаще всего встречается случай, в котором мы выполняем замену, выбирая новую переменную как функцию от старой: t = t ( x ) . Если мы догадались, что подынтегральную функцию можно представить в виде
,
где t′ ( x ) – это производная t по x , то
.

Итак, основную формулу замены переменной можно представить в двух видах.
(1) ,
где x – это функция от t .
(2) ,
где t – это функция от x .

Важное замечание

В таблицах интегралов переменная интегрирования, чаще всего, обозначается как x . Однако стоит учесть, что переменная интегрирования может обозначаться любой буквой. И более того, в качестве переменной интегрирования может быть какое-либо выражение.

В качестве примера рассмотрим табличный интеграл
.

Здесь x можно заменить любой другой переменной или функцией от переменной. Вот примеры возможных вариантов:
;
;
.

В последнем примере нужно учитывать, что при переходе к переменной интегрирования x , дифференциал преобразуется следующим образом:
.
Тогда
.

В этом примере заключена суть интегрирования подстановкой. То есть мы должны догадаться, что
.
После чего интеграл сводится к табличному.
.

Можно вычислить этот интеграл с помощью замены переменной, применяя формулу (2). Положим t = x 2 + x . Тогда
;
;

.

Примеры интегрирования заменой переменной

1) Вычислим интеграл
.
Замечаем, что (sin x )′ = cos x . Тогда

.
Здесь мы применили подстановку t = sin x .

2) Вычислим интеграл
.
Замечаем, что . Тогда

.
Здесь мы выполнили интегрирование заменой переменной t = arctg x .

3) Проинтегрируем
.
Замечаем, что . Тогда

. Здесь, при интегрировании, произведена замена переменной t = x 2 + 1 .

Линейные подстановки

Пожалуй, самыми распространенными являются линейные подстановки. Это замена переменной вида
t = ax + b ,
где a и b – постоянные. При такой замене дифференциалы связаны соотношением
.

Примеры интегрирования линейными подстановками

B) Найти интеграл
.
Решение.
Воспользуемся свойствами показательной функции.
.
ln 2 – это постоянная. Вычисляем интеграл.

.

C) Вычислить интеграл
.
Решение.
Приведем квадратный многочлен в знаменателе дроби к сумме квадратов.
.
Вычисляем интеграл.

.

D) Найти интеграл
.
Решение.
Преобразуем многочлен под корнем.

.
Интегрируем, применяя метод замены переменной .

.
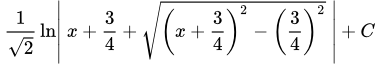
Ранее мы получили формулу
.
Отсюда
.
Подставив это выражение, получим окончательный ответ.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 06-09-2015

Источник

Методы интегрирования

Вычислить первообразные функции мы можем не всегда, но задача на дифференцирование может быть решена для любой функции. Именно поэтому единого метода интегрирования, который можно использовать для любых типов вычислений, не существует.

В рамках данного материала мы разберем примеры решения задач, связанных с нахождением неопределенного интеграла, и посмотрим, для каких типов подынтегральных функций подойдет каждый метод.

Метод непосредственного интегрирования

Основной метод вычисления первообразной функции – это непосредственное интегрирование. Это действие основано на свойствах неопределенного интеграла, и для вычислений нам понадобится таблица первообразных. Прочие методы могут лишь помочь привести исходный интеграл к табличному виду.

Вычислите множество первообразных функции f ( x ) = 2 x + 3 2 · 5 x + 4 3 .

Решение

Для начала изменим вид функции на f ( x ) = 2 x + 3 2 · 5 x + 4 3 = 2 x + 3 2 · 5 x + 4 1 3 .

Мы знаем, что интеграл суммы функций будет равен сумме этих интегралов, значит:

∫ f ( x ) d x = ∫ 3 2 · 5 x + 4 3 = 2 x + 3 2 · 5 x + 4 1 3 d x = ∫ 3 2 · 5 x + 4 1 3 d x

Выводим за знак интеграла числовой коэффициент:

∫ f ( x ) d x = ∫ 2 x d x + ∫ 3 2 ( 5 x + 4 ) 1 3 d x = = ∫ 2 x d x + 2 3 · ∫ ( 5 x + 4 ) 1 3 d x

Чтобы найти первый интеграл, нам нужно будет обратиться к таблице первообразных. Берем из нее значение ∫ 2 x d x = 2 x ln 2 + C 1

Чтобы найти второй интеграл, потребуется таблица первообразных для степенной функции ∫ x p · d x = x p + 1 p + 1 + C , а также правило ∫ f k · x + b d x = 1 k · F ( k · x + b ) + C .

Следовательно, ∫ f ( x ) d x = ∫ 2 x d x + 3 2 · ∫ 5 x + 4 1 3 d x = = 2 x ln 2 + C 1 + 3 2 · 3 20 · ( 5 x + 4 ) 4 3 + C 2 = = 2 x ln 2 + 9 40 · 5 x + 4 4 3 + C

У нас получилось следующее:

∫ f ( x ) d x = ∫ 2 x d x + 3 2 · ∫ 5 x + 4 1 3 d x = = 2 x ln 2 + C 1 + 3 2 · 3 20 · ( 5 x + 4 ) 4 3 + C 2 = = 2 x ln 2 + 9 40 · 5 x + 4 4 3 + C

причем C = C 1 + 3 2 C 2

Ответ: ∫ f ( x ) d x = 2 x ln 2 + 9 40 · 5 x + 4 4 3 + C

Непосредственному интегрированию с применением таблиц первообразных мы посвятили отдельную статью. Рекомендуем вам ознакомиться с ней.

Метод подстановки

Такой метод интегрирования заключается в выражении подынтегральной функции через новую переменную, введенную специально для этой цели. В итоге мы должны получить табличный вид интеграла или просто менее сложный интеграл.

Этот метод очень полезен, когда нужно интегрировать функции с радикалами или тригонометрические функции.

Вычислите неопределенный интеграл ∫ 1 x 2 x — 9 d x .

Решение

Добавим еще одну переменную z = 2 x — 9 . Теперь нам нужно выразить x через z :

z 2 = 2 x — 9 ⇒ x = z 2 + 9 2 ⇒ d x = d z 2 + 9 2 = z 2 + 9 2 ‘ d z = 1 2 ·2 z d z = z d z

Далее подставляем полученные выражения в исходный интеграл и получаем:

∫ d x x 2 x — 9 = ∫ z d z z 2 + 9 2 · z = 2 ∫ d z z 2 + 9

Берем таблицу первообразных и узнаем, что 2 ∫ d z z 2 + 9 = 2 3 a r c t g z 3 + C .

Теперь нам нужно вернуться к переменной x и получить ответ:

2 3 a r c t g z 3 + C = 2 3 a r c t g 2 x — 9 3 + C

Ответ: ∫ 1 x 2 x — 9 d x = 2 3 a r c t g 2 x — 9 3 + C .

Если нам приходится интегрировать функции с иррациональностью вида x m ( a + b x n ) p , где значения m , n , p являются рациональными числами, то важно правильно составить выражение для введения новой переменной. Подробнее об этом читайте в статье, посвященной интегрированию иррациональных функций.

Как мы говорили выше, метод подстановки удобно использовать, когда требуется интегрировать тригонометрическую функцию. Например, с помощью универсальной подстановки можно привести выражение к дробно рациональному виду.

Этот метод объясняет правило интегрирования ∫ f ( k · x + b ) d x = 1 k · F ( k · x + b ) + C .

Добавляем еще одну переменную z = k · x + b . У нас получается следующее:

x = z k — b k ⇒ d x = d z k — b k = z k — b k ‘ d z = d z k

Теперь берем получившиеся выражения и добавляем их в интеграл, заданный в условии:

∫ f ( k · x + b ) d x = ∫ f ( z ) · d z k = 1 k · ∫ f ( z ) d z = = 1 k · F z + C 1 = F ( z ) k + C 1 k

Если же мы примем C 1 k = C и вернемся к исходной переменной x , то у нас получится:

F ( z ) k + C 1 k = 1 k · F k x + b + C

Метод подведения под знак дифференциала

Это метод основывается на преобразовании подынтегрального выражения в функцию вида f ( g ( x ) ) d ( g ( x ) ) . После этого мы выполняем подстановку, вводя новую переменную z = g ( x ) , находим для нее первообразную и возвращаемся к исходной переменной.

∫ f ( g ( x ) ) d ( g ( x ) ) = g ( x ) = z = ∫ f ( z ) d ( z ) = = F ( z ) + C = z = g ( x ) = F ( g ( x ) ) + C

Чтобы быстрее решать задачи с использованием этого метода, держите под рукой таблицу производных в виде дифференциалов и таблицу первообразных, чтобы найти выражение, к которому надо будет приводится подынтегральное выражение.

Разберем задачу, в которой нужно вычислить множество первообразных функции котангенса.

Вычислите неопределенный интеграл ∫ c t g x d x .

Решение

Преобразуем исходное выражение под интегралом с помощью основных тригонометрических формул.

c t g x d x = cos s d x sin x

Смотрим в таблицу производных и видим, что числитель можно подвести под знак дифференциала cos x · d x = d ( sin x ) , значит:

c t g x d x = cos x d x sin x = d sin x sin x , т.е. ∫ c t g x d x = ∫ d sin x sin x .

Допустим, что sin x = z , в таком случае ∫ d sin x sin x = ∫ d z z . Согласно таблице первообразных, ∫ d z z = ln z + C . Теперь вернемся к исходной переменной ∫ d z z = ln z + C = ln sin x + C .

Все решение в кратком виде можно записать так:

∫ с t g x d x = ∫ cos x d x sin x = ∫ d sin x sin x = s i n x = t = = ∫ d t t = ln t + C = t = sin x = ln sin x + C

Ответ: ∫ с t g x d x = ln sin x + C

Метод подведения под знак дифференциала очень часто используется на практике, поэтому советуем вам прочесть отдельную статью, посвященную ему.

Метод интегрирования по частям

Этот метод основывается на преобразовании подынтегрального выражения в произведение вида f ( x ) d x = u ( x ) · v ‘ x d x = u ( x ) · d ( v ( x ) ) , после чего применяется формула ∫ u ( x ) · d ( v ( x ) ) = u ( x ) · v ( x ) — ∫ v ( x ) · d u ( x ) . Это очень удобный и распространенный метод решения. Иногда частичное интегрирование в одной задаче приходится применять несколько раз до получения нужного результата.

Разберем задачу, в которой нужно вычислить множество первообразных арктангенса.

Вычислите неопределенный интеграл ∫ a r c t g ( 2 x ) d x .

Решение

Допустим, что u ( x ) = a r c t g ( 2 x ) , d ( v ( x ) ) = d x , в таком случае:

d ( u ( x ) ) = u ‘ ( x ) d x = a r c t g ( 2 x ) ‘ d x = 2 d x 1 + 4 x 2 v ( x ) = ∫ d ( v ( x ) ) = ∫ d x = x

Когда мы вычисляем значение функции v ( x ) , прибавлять постоянную произвольную С не следует.

Далее используем формулу интегрирования по частям и получаем:

∫ a r c t g ( 2 x ) d x = u ( x ) · v ( x ) — ∫ v ( x ) d ( u ( x ) ) = = x · a r c t g ( 2 x ) — ∫ 2 x d x 1 + 4 x 2

Получившийся интеграл вычисляем, используя метод подведения под знак дифференциала.

Поскольку ∫ a r c t g ( 2 x ) d x = u ( x ) · v ( x ) — ∫ v ( x ) d ( u ( x ) ) = x · a r c t g ( 2 x ) — ∫ 2 x d x 1 + 4 x 2 , тогда 2 x d x = 1 4 d ( 1 + 4 x 2 ) .

∫ a r c t g ( 2 x ) d x = x · a r c t g ( 2 x ) — ∫ 2 x d x 1 + 4 x 2 = = x · a r c t g ( 2 x ) — 1 4 ln 1 + 4 x 2 + C 1 = = x · a r c t g ( 2 x ) — 1 4 ln 1 + 4 x 2 + C

Ответ: ∫ a r c t g ( 2 x ) d x = x · a r c t g ( 2 x ) — 1 4 ln 1 + 4 x 2 + C .

Главная сложность применения такого метода – это необходимость выбирать, какую часть брать за дифференциал, а какую – за функцию u ( x ) . В статье, посвященной методу интегрирования по частям, даны некоторые советы по этому вопросу, с которыми следует ознакомиться.

Если нам требуется найти множество первообразных дробно рациональной функции, то нужно сначала представить подынтегральную функцию в виде суммы простейших дробей, а потом интегрировать получившиеся дроби. Подробнее см. статью об интегрировании простейших дробей.

Если мы интегрируем степенное выражение вида sin 7 x · d x или d x ( x 2 + a 2 ) 8 , то нам будут полезны рекуррентные формулы, которые могут постепенно понижать степень. Они выводятся с помощью последовательного многократного интегрирования по частям. Советуем прочитать статью «Интегрирование с помощью рекуррентных формул.

Подведем итоги. Для решения задач очень важно знать метод непосредственного интегрирования. Другие методы (подведение под знак дифференциала, подстановка, интегрирование по частям) также позволяют упростить интеграл и привести его к табличному виду.

Источник

Лекция 2. Замена переменной и и интегрирование по частям в неопределенном интеграле

Сайт:	Навчальний сайт ХНАДУ
Курс:	Вища Математика (2 семестр) Вишневецький А.Л.
Книга:	Лекция 2. Замена переменной и и интегрирование по частям в неопределенном интеграле

Надруковано:	Гість
Дата:	четвер 18 листопад 2021 16:09

Зміст

Тема 1. Неопределенный интеграл, его свойства

1. Первообразная

Пусть f ( x ) – данная функция.

Определение . Функция F ( x ) называется первообразной для f ( x ) , если

Примеры . x 2 – первообразная для 2 x , т.к. ( x 2 )’ = 2 x . Впрочем, x 2 + 1 и x 2 — 5 – тоже первообразные для 2 x , т.к. ( x 2 + 1)’ = 2 x и ( x 2 — 5)’ = 2 x .

Теорема 1. Если F ( x ) – первообразная для f ( x ) , то

1) F ( x ) + С – тоже первообразная для f ( x ) .

2) Любая первообразная для f ( x ) имеет вид F ( x ) + С для некоторого С.

2. Неопределенный интеграл

Определение . Множество всех первообразных функции f ( x ) называется неопределенным интегралом от этой функции и обозначается так:

Здесь f ( x) dx – подынтегральное выражение, f ( x ) – подынтегральная функция, x – переменная интегрирования.

Если функция непрерывна на некотором отрезке, то на этом отрезке существует её неопределенный интеграл.

Операции нахождения дифференциала и неопределенного интеграла – взаимно обратные:

3. Свойства неопределенного интеграла

Формул «интеграл от произведения» и «интеграл от частного» функций нет.

4. Таблица первообразных

Таблица проверяется с помощью (1). Формулы № 10, 12, 14 есть обобщение формул № 9, 11, 13. В формулах № 10, 12, 14, 15 a ≠ 0 .

Полная запись формулы №1:

Тема 2. Основные методы интегрирования

5. Интегрирование подстановкой (заменой переменной)

Суть метода: путем введения новой переменной интегрирования (т.е. подста­новки) свести данный интеграл к более простому (желательно – к табличному).

Начнем с формулы замены. Надо найти интеграл

Сделаем подстановку φ(t) = x , где φ(t) — функция, имеющая непрерывную производную. По определению дифференциала, dx = φ'(t)dt . Подставляем в (1):

– формула замены переменной в неопределенном интеграле. После ее примене­ния и вычисления полученного интеграла нужно вернуться к исходной перемен­ной. Формулу (2) применяют как «слева направо», так и «справа налево». Общих методов подбора подстановок не существует.

6. Интегрирование по частям

Теорема . Если функции u = u(x) , ν = ν (x) имеют непрерывные производные, то

Док-во . Интегрируя равенство d(uv) = udv + vdu , получим uv = ∫ udv — ∫ vdu , т.е. (5)

Формула (5) сводит нахождение ∫ udv к нахождению ∫ vdu , поэтому ее приме­няют тогда, когда последний интеграл не сложнее первого. Для применения этой формулы подынтегральное выражение представляют как произведение двух сомножителей, один из которых обозначают u , другой dv . Затем u дифференцируют (находят du ), а dv интегрируют (находят v ).

Укажем способ выбора u и dv в двух типичных случаях. Пусть P(x) – многочлен.

Формулу (5) можно применять повторно. Например, в случае а) это делают n раз, где n – степень многочлена P(x) .

7. Интегрирование простейших рациональных дробей

Простейшие рациональные дроби – это дроби:

1 рода: ( k N ) и 2 рода: (дискриминант знаменателя D n = 1 так:

• Заменить

• Разложить интеграл в сумму вида

К первому интегралу применить формулу (4), а второй – табличный (арктангенс).

Источник