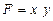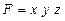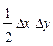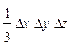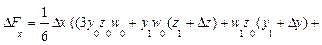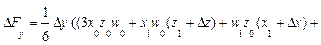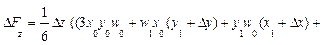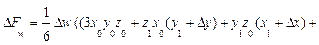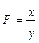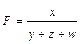Интегральный способ детерминированного факторного анализа
Как известно, в детерминированном факторном анализе используют следующие основные способы:
- способ цепных подстановок;
- способ абсолютных разниц;
- способ относительных (процентных) разниц;
- интегральный метод и др.
Интегральный метод позволяет достигнуть полного разложения результативного показателя по факторам и носит универсальный характер – применяется для измерения влияния факторов в мультипликативных, кратных и смешанных моделях.
Использование этого способа позволяет получить более точные результаты по сравнению с остальными выше названными способами, поскольку дополнительный прирост результативного показателя от взаимодействия факторов присоединяется не к последнему фактору, а делится поровну между ними.
Рассмотрим алгоритмы расчетов влияния факторов для различных моделей, приводимые в специальной литературе:
- Мультипликативная модель вида f = x*y:
Δf(x) = Δx*y0 + ½Δx*Δy, или Δf(x) = ½Δx (y0 + y1);
Δf(y) = Δy*x0 + ½Δx*Δy, или Δf(y) = ½Δy (x0 + x1);
где x0, y0 – базисные (плановые) значения факторов, оказывающих влияние на результативный показатель; x1, y1 — фактические значения факторов; Δx = x1-x0, Δy = y1-y0 — абсолютные изменения (отклонения) факторов х, у соответственно;
Мультипликативная модель вида f = x*y*z:
Δf(x) = ½Δx (y0*z1 + y1*z0) + ⅓Δx*Δy*Δz;
Δf(y) = ½Δy (x0*z1 + x1*z0) + ⅓Δx*Δy*Δz;
Δf(z) = ½Δz (x0*y1 + x1*y0) + ⅓Δx*Δy*Δz;
Кратная модель вида f = x/y:
Δf(x) = Δx/Δy * ln |y1/y0|;
Δf(y) = Δf — Δf(x) = (f1-f0) — Δf(x);
Смешанная модель вида f = x/(y+z):
Δf(x) = Δx/(Δy+Δz) * ln |(y1+z1)/(y0+z0)|;
Δf(y) = (Δf — Δf(x))Δy / (Δy+Δz);
Δf(z) = (Δf — Δf(x))Δz / (Δy+Δz).
Пример применения интегрального способа для факторного анализа
Порядок применения интегрального способа рассмотрим на следующем примере. Проанализировать влияние на валовый объем производства количества работников и их выработки интегральным способом. Исходные данные представлены в таблице.
| Показатель | Условное обозначение | Базисное значение (0) | Фактическое значение (1) | Изменение (+,-) | |
| Абсолютное | Относительное, % | ||||
| Объем валовой продукции, тыс. руб. | ВП | 2920 | 3400 | +480 | 16,40 |
| Среднесписочная численность персонала, чел. | ЧР | 20 | 25 | +5 | 25,00 |
| Среднегодовая выработка продукции одним работником, тыс. руб. | ГВ | 146 | 136 | -10 | -6,85 |
Решение. Зависимость объема производства продукции от данных факторов можно описать с помощью двухфакторной мультипликативной модели: ВП = ЧР * ГВ.
Алгоритм расчета влияния факторов интегральным способом таков:
- ΔВП(ЧР) = ΔЧР*ГВ0+½ΔЧР*ΔГВ = 5*146+0,5*5*(-10) = 705 тыс. руб. — влияние изменения численности персонала на объем производства;
- ΔВП(ГВ) = ΔГВ*ЧР0+½ΔЧР*Δ(-10) = -10*20+0,5*5*(-10) = -225 тыс. руб. — влияние изменения среднегодовой выработки продукции одним работником на объем производства;
- ΔВП = ΔВП(ЧР)+ ΔВП(ГВ) = 705 + (-225) = 480 тыс. руб. — суммарное влияние двух факторов.
Таким образом, использование интегрального метода знания основ интегрирования. Достаточно в готовые рабочие формулы подставить числовые данные и сделать расчеты.
Источник
Решения интегральных уравнений онлайн
В этом разделе мы рассмотрим типовые задачи по интегральным уравнениям с решениями. Интегральное уравнение содержит неизвестную функцию под знаком интеграла (по аналогии как дифференциальное — функцию под знаком дифференциала:)).
Выделяют два основных класса интегральных уравнений: уравнения Фредгольма I и II рода:
$$ (I) \quad \int_a^b K(x,s)u(s)ds = f(x),\\ (II) \quad u(x)=\int_a^b K(x,s)u(s)ds + f(x). $$
В случае переменного верхнего предела интегрирования получаем соответственно уравнение Вольтерра I и II рода:
$$ (I) \quad \int_a^x K(x,s)u(s)ds = f(x),\\ (II) \quad u(x)=\int_a^x K(x,s)u(s)ds + f(x). $$
Это линейные неоднородные уравнения (при $f(x)=0$ — однородные), иногда рассматриваются более общий случай с параметром $\lambda$ перед интегралом.
Ниже вы найдете примеры нахождения решений интегральных уравнений, собственных значений и функций, исследования ядра, применения интегральных уравнений для решения других задач.
Примеры решений интегральных уравнений
Задача 1. Пользуясь теоремой Гильберта-Шмидта, исследовать и решить интегральное уравнение 2-го рода $(E+\lambda A)x=y$ в гильбертовом пространстве $X$.
Задача 2. Найти собственные значения и собственные функции уравнения:
$$ y(x)=\lambda \int_0^1 (\cos 2\pi x +2x \sin 2\pi t +t \sin \pi x)y(t)dt. $$
Задача 3. Решить уравнение Вольтерры, сведя его к обыкновенному дифференциальному уравнению.
Задача 4. Решить или установить неразрешимость уравнений с вырожденным ядром.
Задача 5. Решить интегральное уравнение, сведя его предварительно к обыкновенному дифференциальному уравнению.
Задача 6. Найти резольвенту для интегрального уравнения Вольтерры со следующим ядром $K(x,t)=x^<1>t^<2>$.
Задача 7. Исследовать решения уравнения с вырожденным ядром при различных значениях параметра $\lambda$ (ограничиться случаем вещественных характеристических чисел).
$$ y(x)-\lambda \int_0^1 x y(t)dt = \sin 2\pi x. $$
Задача 8. Для симметричного ядра $$K(x,t) = \frac<1> <2>\sin |x-t| \quad (0 \le, x,t \le \pi)$$ найти характеристические числа и соответствующие им собственные функции, сводя интегральное уравнение к однородной краевой задаче для обыкновенного дифференциального уравнения.
Задача 9. Решить краевую задачу, используя функцию Грина
Задача 10. Применяя преобразование Лапласа, решить интегральное уравнение
Помощь с интегральными уравнениями
Если вам нужна помощь с решением задач и контрольных по интегральным уравнениям (и другим разделам математического и функционального анализа), обращайтесь в МатБюро. Стоимость подробной консультации от 200 рублей , оформление производится в Word, срок от 1 дня.
Источник
Интегральный метод



Интегральный метод применяется для измерения влияния факторов в мультипликативных, кратных и смешанных кратно-аддитивных моделях. Метод называется так потому, что для получения его формул использовалось интегральное исчисление. Самое важное, что следует знать об интегральном методе – это то, что он позволяет получать более точные результаты расчета влияния факторов по сравнению с методом цепных подстановок, индексным методом, методами абсолютных и относительных разниц, а также по сравнению с другими методами, которые мы называли в начале этой главы (кроме логарифмического метода). Причина в том, что в этих методах общее приращение результативного показателя представляется как сумма его приращений под влиянием изолированных друг от друга факторов. Например, если результирующий показатель F зависит от трех факторов: х, у и z, – то его приращение представляется как сумма трех приращений:
На самом же деле факторы действуют не изолированно, они взаимодействуют друг с другом и влияют на результирующий показатель совместно, из-за чего происходит дополнительный прирост результирующего показателя, который можно обозначить, как DF x, y, z , так что на самом деле приращение F представляет собой сумму четырех приращений:
По справедливости, приращение из-за взаимодействия факторов (DF x, y, z ) должно быть распределено между оценками влияния всех факторов (в данном примере между DF x ,DF y иDF z ). Но особенность формул МЦП, МАР, МОР и индексного метода в том, что это приращение не распределяется, а присоединяется к приросту результативного показателя под влиянием того фактора, который находится в модели на последнем месте (в данном примере – к величине DF z ). Соответственно, влияние последнего фактора завышается, а остальных – занижается. Таким образом, индексный метод, методы цепных подстановок, абсолютных и относительных разниц несут в себе погрешность, они дают неточные результаты. Кстати, из-за того, что величина DF x, y, z в этих методах не распределяется между оценками факторов, она была названа неразложимым остатком.
В интегральном методе эта неточность устраняется за счет того, что дополнительный прирост результативного показателя от взаимодействия факторов (неразложимый остаток) делится поровну между оценками влияния всех факторов (раскладывается). Из-за этого интегральный метод дает точные и единообразные результаты, которые не зависят от местоположения факторов в модели. Соответственно, при использовании интегрального метода для мультипликативных моделей не требуется предварительная классификация и расстановка факторов в определенном порядке.
Приведем формулы интегрального метода для мультипликативных моделей. Для двухфакторных моделей
формулы оценок влияния факторов выглядят следующим образом:
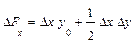
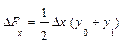
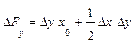
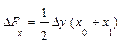
На примере этих формул становится понятно, почему интегральный метод дает единообразные результаты, которые не зависят от места факторов в модели. Формулы расчета оценок обоих факторов абсолютно идентичны. Если записать модель в виде:
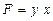
и, соответственно, заменить в формулах расчета оценок факторов х на у, а у – на х, то получим такие же две формулы, как исходные (и такие же результаты расчета по ним).
Для трехфакторных моделей
формулы имеют вид:
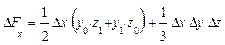
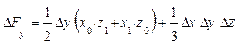
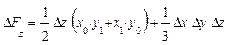
Обратим внимание читателей на последние слагаемые приведенных формул
в формулах для двухфакторной модели и
в формулах для трехфакторной модели. Эти слагаемые представляют собой неразложимый остаток, который разделен поровну, по числу факторов в этих моделях (соответственно, на 2 и 3 части) и присоединен равными частями к оценкам влияния каждого из факторов.
Приведем формулы интегрального метода для четырехфакторных моделей вида
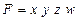
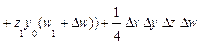
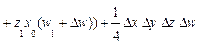
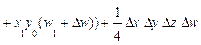
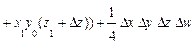
Как видим, в этих формулах неразложимый остаток разделен на четыре части и также поровну распределен между оценками влияния всех факторов.
Интегральный метод, в принципе, применим к мультипликативным моделям и с большим количеством факторов, но его формулы для таких моделей очень громоздки, и пользоваться ими для расчетов «вручную» слишком трудоемко.

Формулы интегрального метода для кратных моделей
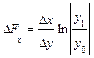
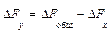
Прямые скобки означают, что выражение под знаком логарифма нужно брать по модулю.
Приведем формулы интегрального метода для смешанных моделей вида
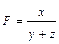
Эти формулы имеют вид:
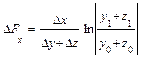
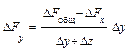
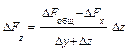
Для смешанных моделей вида
формулы интегрального метода – следующие:
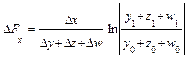
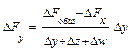
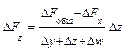
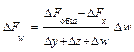
Как видим, использование интегрального метода не требует знания процесса интегрирования, его рабочие формулы требуют только знания арифметики и умения вычислять натуральные логарифмы (что несложно даже с помощью калькулятора). В конце решения прямой задачи факторного анализа интегральным методом, как и в остальных методах, требуется проверка в виде сложения оценок влияния всех факторов и сравнения этой суммы с общим приращением результирующего показателя.
Рассмотрим применение интегрального метода на данных примера 1 из пункта 5.3 (табл. 5.8).
Источник