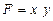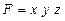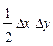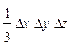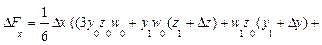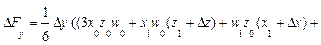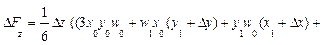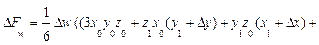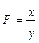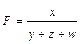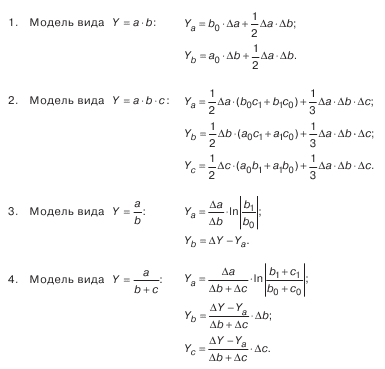Интегральный метод



Интегральный метод применяется для измерения влияния факторов в мультипликативных, кратных и смешанных кратно-аддитивных моделях. Метод называется так потому, что для получения его формул использовалось интегральное исчисление. Самое важное, что следует знать об интегральном методе – это то, что он позволяет получать более точные результаты расчета влияния факторов по сравнению с методом цепных подстановок, индексным методом, методами абсолютных и относительных разниц, а также по сравнению с другими методами, которые мы называли в начале этой главы (кроме логарифмического метода). Причина в том, что в этих методах общее приращение результативного показателя представляется как сумма его приращений под влиянием изолированных друг от друга факторов. Например, если результирующий показатель F зависит от трех факторов: х, у и z, – то его приращение представляется как сумма трех приращений:
На самом же деле факторы действуют не изолированно, они взаимодействуют друг с другом и влияют на результирующий показатель совместно, из-за чего происходит дополнительный прирост результирующего показателя, который можно обозначить, как DF x, y, z , так что на самом деле приращение F представляет собой сумму четырех приращений:
По справедливости, приращение из-за взаимодействия факторов (DF x, y, z ) должно быть распределено между оценками влияния всех факторов (в данном примере между DF x ,DF y иDF z ). Но особенность формул МЦП, МАР, МОР и индексного метода в том, что это приращение не распределяется, а присоединяется к приросту результативного показателя под влиянием того фактора, который находится в модели на последнем месте (в данном примере – к величине DF z ). Соответственно, влияние последнего фактора завышается, а остальных – занижается. Таким образом, индексный метод, методы цепных подстановок, абсолютных и относительных разниц несут в себе погрешность, они дают неточные результаты. Кстати, из-за того, что величина DF x, y, z в этих методах не распределяется между оценками факторов, она была названа неразложимым остатком.
В интегральном методе эта неточность устраняется за счет того, что дополнительный прирост результативного показателя от взаимодействия факторов (неразложимый остаток) делится поровну между оценками влияния всех факторов (раскладывается). Из-за этого интегральный метод дает точные и единообразные результаты, которые не зависят от местоположения факторов в модели. Соответственно, при использовании интегрального метода для мультипликативных моделей не требуется предварительная классификация и расстановка факторов в определенном порядке.
Приведем формулы интегрального метода для мультипликативных моделей. Для двухфакторных моделей
формулы оценок влияния факторов выглядят следующим образом:
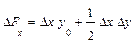
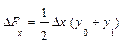
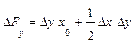
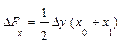
На примере этих формул становится понятно, почему интегральный метод дает единообразные результаты, которые не зависят от места факторов в модели. Формулы расчета оценок обоих факторов абсолютно идентичны. Если записать модель в виде:
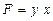
и, соответственно, заменить в формулах расчета оценок факторов х на у, а у – на х, то получим такие же две формулы, как исходные (и такие же результаты расчета по ним).
Для трехфакторных моделей
формулы имеют вид:
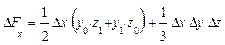
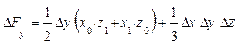
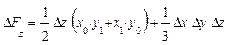
Обратим внимание читателей на последние слагаемые приведенных формул
в формулах для двухфакторной модели и
в формулах для трехфакторной модели. Эти слагаемые представляют собой неразложимый остаток, который разделен поровну, по числу факторов в этих моделях (соответственно, на 2 и 3 части) и присоединен равными частями к оценкам влияния каждого из факторов.
Приведем формулы интегрального метода для четырехфакторных моделей вида
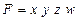
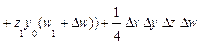
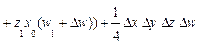
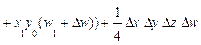
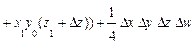
Как видим, в этих формулах неразложимый остаток разделен на четыре части и также поровну распределен между оценками влияния всех факторов.
Интегральный метод, в принципе, применим к мультипликативным моделям и с большим количеством факторов, но его формулы для таких моделей очень громоздки, и пользоваться ими для расчетов «вручную» слишком трудоемко.

Формулы интегрального метода для кратных моделей
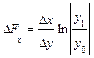
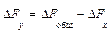
Прямые скобки означают, что выражение под знаком логарифма нужно брать по модулю.
Приведем формулы интегрального метода для смешанных моделей вида
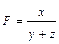
Эти формулы имеют вид:
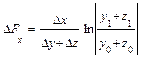
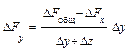
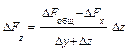
Для смешанных моделей вида
формулы интегрального метода – следующие:
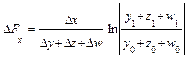
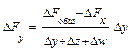
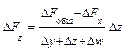
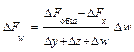
Как видим, использование интегрального метода не требует знания процесса интегрирования, его рабочие формулы требуют только знания арифметики и умения вычислять натуральные логарифмы (что несложно даже с помощью калькулятора). В конце решения прямой задачи факторного анализа интегральным методом, как и в остальных методах, требуется проверка в виде сложения оценок влияния всех факторов и сравнения этой суммы с общим приращением результирующего показателя.
Рассмотрим применение интегрального метода на данных примера 1 из пункта 5.3 (табл. 5.8).
Источник
Изучаем порядок проведения измерений интегральным способом и способы логарифмирования
Определить степень воздействия конкретных факторов на жизнь компании в целом или ее отдельные стороны, показатели, можно с помощью факторного анализа. Главное, грамотно подобрать метод и использовать его во благо.
Определить степень воздействия конкретных факторов на жизнь компании в целом или ее отдельные стороны, показатели, можно с помощью факторного анализа. Главное, грамотно подобрать метод и использовать его во благо.
Экономисты и аналитики успешно применяют результаты факторного анализа в целях оптимизации производства и работы отдельных отделов, повышения показателей прибыльности и эффективности. Результаты таких исследований позволяют направить силы точечно, исключительно на те моменты и факты, которые ухудшают или затормаживают развитие. Освоение всех методов оценки ситуации и факторов изучают учащиеся ВУЗов по экономическому профилю.
Одним из универсальных способов оценки воздействия параметров и условий (обстоятельств и решений) на конкретные моменты или деятельность организации в целом является интегральный или логарифмический.
Особенности интегрального метода
Данный способ помогает определить степень воздействия факторов на отдельные стороны и показатели жизнедеятельности любой компании. Он применим в отношении мультипликативных, кратных и смешанных моделей. В большинстве случаев методика активно используется в тех случаях, когда результативный показатель можно представить в виде функции с несколькими аргументами.
Достоинством интегрального метода является то, что он помогает получить более точные результаты на фоне упрощения сложных функций. Использование правил интегрирования сводится к применению стандартных математических правил.
Важно отметить, что интегральный метод основывается не просто на проведении соответствующих операций над функциями, но и использовании рабочих формул, в которые достаточно подставить числа, что упрощает поведение факторного анализа и получение точных результатов. «Рабочие формулы» можно найти в специальной литературе (по математике высшей математике) и успешно пользоваться ими.
Результаты расчетов при интегральном методе не зависят от расположения факторов. Также особенностью интегрального метода является то, что дополнительный прирост итогового показателя равномерно распределяется между всеми факторами, что позволяет получить более взвешенный аналитический вывод.
Источник
IX Международная студенческая научная конференция Студенческий научный форум — 2017
ИНТЕГРАЛЬНЫЙ МЕТОД В АНАЛИЗЕ ХОЗЯЙСТВЕННОЙ ДЕЯТЕЛЬНОСТИ
аддитивные модели (баланс товарной продукции);
мультипликативные модели (двухфакторная модель, выражающая зависимость между объемом выпуска продукции, количеством единиц оборудования и выработкой продукции в расчете на одну единицу оборудования);
кратные модели (формула, которая выражает зависимость между продолжительностью оборота оборотных активов в днях, средней величиной этих активов за данный период и однодневным объемом продаж);
смешанные модели (показатель рентабельности активов, на уровень которого влияют три фактора: чистая прибыль, величина внеоборотных активов, величина оборотных активов).
Вначале необходимо построить экономико-математическую модель, которая будет описывать влияние отдельных факторов на обобщающие экономические показатели деятельности организации. В анализе хозяйственной деятельности большое распространение получили многофакторные мультипликативные модели, именно они позволяют изучить влияние значительного количества факторов на обобщающие показатели. Это поможет достичь большей глубины и точности анализа.
После построения экономико-математической модели необходимо выбрать способ её решения. Есть ряд традиционных способов: цепных подстановок, балансовый, абсолютных и относительных границ, индексный метод, а также методы корреляционно-регрессионного, кластерного, дисперсионного анализа. Но наряду с ними в экономическом анализе используются и специфически математические методы и способы. Одним их таких методов является интегральный. Он направлен на определение влияния отдельных факторов с использованием мультипликативных, кратных кратно-аддитивных моделей.
При применении интегрального метода имеется возможность получить более обоснованные результаты исчисления влияния отдельных факторов, чем при использовании метода цепных подстановок и его вариантов. Эти методы имеют следующий ряд недостатков:
Результаты расчетов влияния факторов зависят от принятой последовательности замены базисных величин отдельных факторов на фактические величины;
Дополнительный прирост обобщающего показателя, вызванный взаимодействием факторов, в виде неразложимого остатка присоединяется к сумме влияния последнего фактора
Если же использовать интегральный метод, то прирост делится поровну между всеми факторами.Интегральный метод устанавливает общий подход к решению моделей различных видов, независимо от числа элементов, которые входят в данную модель, и формы связи между этими элементами.
В основе интегрального метода факторного анализа лежит суммирование приращений функций, определенной как частная производная, умноженная на приращение аргумента на бесконечно малых промежутках. При применении интегрального метода необходимо соблюдать следующие условия:
должно соблюдаться условие непрерывной дифференцируемости функции, где в качестве аргумента берется какой-либо экономический показатель;
функция между начальной и конечной точками элементарного периода должна изменяться по прямой;
должно иметь место постоянство соотношений скоростей изменения величин факторов
При использовании интегрального метода исчисления определенного интеграла по заданной подынтегральной функции и заданному интервалу интегрирования осуществляется по имеющейся стандартной программе с применением современных средств вычислительной техники.При осуществлении решения мультипликативной модели для расчета влияния отдельных факторов на обобщающий экономический показатель можно использовать следующие формулы:
При решении кратной модели для расчета влияния факторов воспользуемся формулами:
ΔZ(x) = Δx/Δy Ln y1/y0
Есть два основных типа задач, которые решаются при помощи интегрального метода: динамический и статистический. При статистическом отсутствует информация об изменении анализируемых факторов в течение данного периода. Примером такой задачи может быть анализ выполнения бизнес-планов либо анализ изменения экономических показателей по сравнению с предыдущим периодом. Динамический же тип задач имеет место в условиях наличия информации об изменении анализируемых факторов в течение данного периода. К такому типу задач можно отнести вычисления, связанные с изучением временных рядов экономических показателей.
Рассмотрим на примере преимущество интегрального метода.
Источник