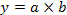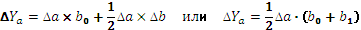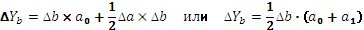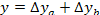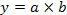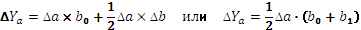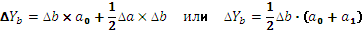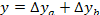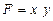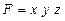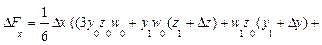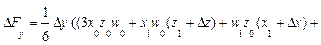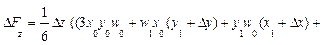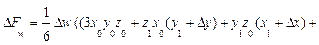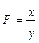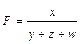Интегральный способ в анализе хозяйственной деятельности



Элиминирование как способ детерминированного факторного анализа имеет существенный недостаток, так как при его использовании исходят из того, что факторы изменяются независимо друг от друга. На самом же деле они изменяются совместно, взаимосвязанно, и от этого взаимодействия получается дополнительный прирост результативного показателя, который при использовании приема элиминирования присоединяется к одному из факторов, как правило, последнему. В связи с этим величина влияния факторов на изменение результативного показателя меняется в зависимости от месторасположения фактора в детерминированной факторной модели. Для устранения указанного недостатка используются интегральный способ и способ логарифмирования.
Интегральный способ применяется для измерения влияния факторов на изменение результативного показателя в мультипликативных, кратных и смешанных кратно-аддитивных моделях.
Использование данного способа позволяет получать более точные результаты расчета влияния факторов по сравнению со способами элиминирования, так как дополнительный прирост результативного показателя от взаимодействия факторов присоединяется не к последнему фактору, а делится поровну между ними.
Алгоритм расчета влияния факторов на изменение результативного показателя в двухфакторной мультипликативной модели интегральным способом включает следующие этапы.
1 этап. Построение факторной модели результативного показателя:
где у — результативный показатель;
а, b — факторные показатели, имеющие с результативным показателем мультипликативную зависимость.
2 этап. Определение абсолютного изменения результативного показателя:
базисное значение результативного показателя:у0 = а0 ∙ b0;
фактическое значение результативного показателя: у1 = а1 ∙ b1
3 этап. Расчет влияния факторов на абсолютное изменение результативного показателя:
4 этап. Проведение балансовой увязки полученных результатов:
∆
5 этап. Формулирование выводов по результатам проведенного анализа.
Для расчета влияния факторов на изменение результативного показателя в других типах детерминированных факторных моделей используются следующие рабочие формулы, приведенные в таблице 6.1.
Таким образом, использование интегрального способа не требует знания всего процесса интегрирования. Достаточно в готовые рабочие формулы подставить необходимые числовые данные и произвести расчеты с помощью калькулятора или ПЭВМ в Ехсе1.
Таблица 6.1 – Алгоритм расчета влияния факторов интегральным способом
| Вид факторной модели | Алгоритм расчета влияния факторов |
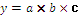 | 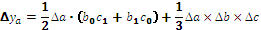 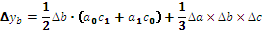 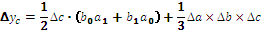 |
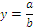 | 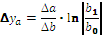 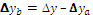 |
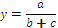 | 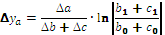 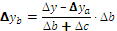 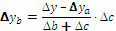 |
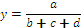 | 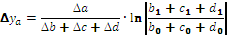 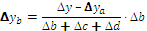 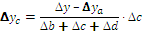 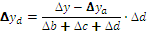 |
Вопросы для самоконтроля:
1. Какие основные приемы используются для измерения влияния факторов в детерминированном факторном анализе?
2. В чем суть способа элиминирования?
3. Какие правила необходимо соблюдать при использовании способа цепной подстановки?
4. В чем суть, область применения и процедура расчетов способами:
5. В чем недостаток способа элиминирования и в каком способе он устраняется?
6. В чем преимущество использования способа логарифмирования?
Источник
Интегральный способ в анализе хозяйственной деятельности
Элиминирование как способ детерминированного факторного анализа имеет существенный недостаток, так как при его использовании исходят из того, что факторы изменяются независимо друг от друга. На самом же деле они изменяются совместно, взаимосвязанно, и от этого взаимодействия получается дополнительный прирост результативного показателя, который при использовании приема элиминирования присоединяется к одному из факторов, как правило, последнему. В связи с этим величина влияния факторов на изменение результативного показателя меняется в зависимости от месторасположения фактора в детерминированной факторной модели. Для устранения указанного недостатка используются интегральный способ и способ логарифмирования.
Интегральный способ применяется для измерения влияния факторов на изменение результативного показателя в мультипликативных, кратных и смешанных кратно-аддитивных моделях.
Использование данного способа позволяет получать более точные результаты расчета влияния факторов по сравнению со способами элиминирования, так как дополнительный прирост результативного показателя от взаимодействия факторов присоединяется не к последнему фактору, а делится поровну между ними.
Алгоритм расчета влияния факторов на изменение результативного показателя в двухфакторной мультипликативной модели интегральным способом включает следующие этапы.
1 этап. Построение факторной модели результативного показателя:
где у — результативный показатель;
а, b — факторные показатели, имеющие с результативным показателем мультипликативную зависимость.
2 этап. Определение абсолютного изменения результативного показателя:
базисное значение результативного показателя:у0 = а0 ∙ b0;
фактическое значение результативного показателя: у1 = а1 ∙ b1
3 этап. Расчет влияния факторов на абсолютное изменение результативного показателя:
4 этап. Проведение балансовой увязки полученных результатов:
∆
5 этап. Формулирование выводов по результатам проведенного анализа.
Для расчета влияния факторов на изменение результативного показателя в других типах детерминированных факторных моделей используются следующие рабочие формулы, приведенные в таблице 6.1.
Таким образом, использование интегрального способа не требует знания всего процесса интегрирования. Достаточно в готовые рабочие формулы подставить необходимые числовые данные и произвести расчеты с помощью калькулятора или ПЭВМ в Ехсе1.
Таблица 6.1 – Алгоритм расчета влияния факторов интегральным способом
| Вид факторной модели | Алгоритм расчета влияния факторов |
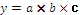 | 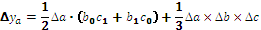 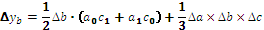 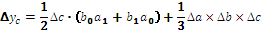 |
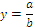 | 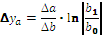 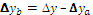 |
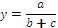 | 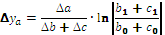 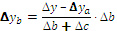 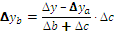 |
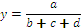 | 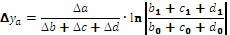 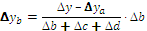 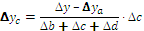 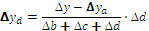 |
Вопросы для самоконтроля:
1. Какие основные приемы используются для измерения влияния факторов в детерминированном факторном анализе?
2. В чем суть способа элиминирования?
3. Какие правила необходимо соблюдать при использовании способа цепной подстановки?
4. В чем суть, область применения и процедура расчетов способами:
5. В чем недостаток способа элиминирования и в каком способе он устраняется?
6. В чем преимущество использования способа логарифмирования?
Источник
Интегральный метод



Интегральный метод применяется для измерения влияния факторов в мультипликативных, кратных и смешанных кратно-аддитивных моделях. Метод называется так потому, что для получения его формул использовалось интегральное исчисление. Самое важное, что следует знать об интегральном методе – это то, что он позволяет получать более точные результаты расчета влияния факторов по сравнению с методом цепных подстановок, индексным методом, методами абсолютных и относительных разниц, а также по сравнению с другими методами, которые мы называли в начале этой главы (кроме логарифмического метода). Причина в том, что в этих методах общее приращение результативного показателя представляется как сумма его приращений под влиянием изолированных друг от друга факторов. Например, если результирующий показатель F зависит от трех факторов: х, у и z, – то его приращение представляется как сумма трех приращений:
На самом же деле факторы действуют не изолированно, они взаимодействуют друг с другом и влияют на результирующий показатель совместно, из-за чего происходит дополнительный прирост результирующего показателя, который можно обозначить, как DF x, y, z , так что на самом деле приращение F представляет собой сумму четырех приращений:
По справедливости, приращение из-за взаимодействия факторов (DF x, y, z ) должно быть распределено между оценками влияния всех факторов (в данном примере между DF x ,DF y иDF z ). Но особенность формул МЦП, МАР, МОР и индексного метода в том, что это приращение не распределяется, а присоединяется к приросту результативного показателя под влиянием того фактора, который находится в модели на последнем месте (в данном примере – к величине DF z ). Соответственно, влияние последнего фактора завышается, а остальных – занижается. Таким образом, индексный метод, методы цепных подстановок, абсолютных и относительных разниц несут в себе погрешность, они дают неточные результаты. Кстати, из-за того, что величина DF x, y, z в этих методах не распределяется между оценками факторов, она была названа неразложимым остатком.
В интегральном методе эта неточность устраняется за счет того, что дополнительный прирост результативного показателя от взаимодействия факторов (неразложимый остаток) делится поровну между оценками влияния всех факторов (раскладывается). Из-за этого интегральный метод дает точные и единообразные результаты, которые не зависят от местоположения факторов в модели. Соответственно, при использовании интегрального метода для мультипликативных моделей не требуется предварительная классификация и расстановка факторов в определенном порядке.
Приведем формулы интегрального метода для мультипликативных моделей. Для двухфакторных моделей
формулы оценок влияния факторов выглядят следующим образом:
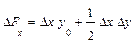
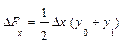
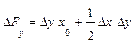
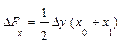
На примере этих формул становится понятно, почему интегральный метод дает единообразные результаты, которые не зависят от места факторов в модели. Формулы расчета оценок обоих факторов абсолютно идентичны. Если записать модель в виде:
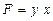
и, соответственно, заменить в формулах расчета оценок факторов х на у, а у – на х, то получим такие же две формулы, как исходные (и такие же результаты расчета по ним).
Для трехфакторных моделей
формулы имеют вид:
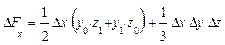
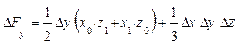
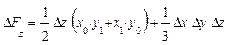
Обратим внимание читателей на последние слагаемые приведенных формул
в формулах для двухфакторной модели и
в формулах для трехфакторной модели. Эти слагаемые представляют собой неразложимый остаток, который разделен поровну, по числу факторов в этих моделях (соответственно, на 2 и 3 части) и присоединен равными частями к оценкам влияния каждого из факторов.
Приведем формулы интегрального метода для четырехфакторных моделей вида
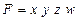
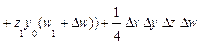
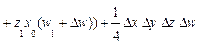
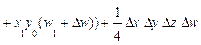
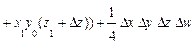
Как видим, в этих формулах неразложимый остаток разделен на четыре части и также поровну распределен между оценками влияния всех факторов.
Интегральный метод, в принципе, применим к мультипликативным моделям и с большим количеством факторов, но его формулы для таких моделей очень громоздки, и пользоваться ими для расчетов «вручную» слишком трудоемко.

Формулы интегрального метода для кратных моделей
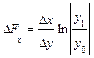
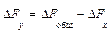
Прямые скобки означают, что выражение под знаком логарифма нужно брать по модулю.
Приведем формулы интегрального метода для смешанных моделей вида
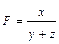
Эти формулы имеют вид:
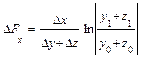
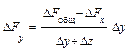
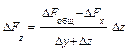
Для смешанных моделей вида
формулы интегрального метода – следующие:
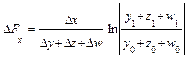
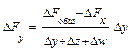
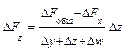
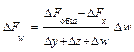
Как видим, использование интегрального метода не требует знания процесса интегрирования, его рабочие формулы требуют только знания арифметики и умения вычислять натуральные логарифмы (что несложно даже с помощью калькулятора). В конце решения прямой задачи факторного анализа интегральным методом, как и в остальных методах, требуется проверка в виде сложения оценок влияния всех факторов и сравнения этой суммы с общим приращением результирующего показателя.
Рассмотрим применение интегрального метода на данных примера 1 из пункта 5.3 (табл. 5.8).
Источник