Интегральный способ экономическом анализе

Интегральный способ детерминированного факторного анализа

Как известно, в детерминированном факторном анализе используют следующие основные способы:

• способ цепных подстановок;
• способ абсолютных разниц;
• способ относительных (процентных) разниц;
• интегральный метод и др.

Интегральный метод позволяет достигнуть полного разложения результативного показателя по факторам и носит универсальный характер – применяется для измерения влияния факторов в мультипликативных, кратных и смешанных моделях.

Использование этого способа позволяет получить более точные результаты по сравнению с остальными выше названными способами, поскольку дополнительный прирост результативного показателя от взаимодействия факторов присоединяется не к последнему фактору, а делится поровну между ними.

Рассмотрим алгоритмы расчетов влияния факторов для различных моделей, приводимые в специальной литературе:

Мультипликативная модель вида f = x*y:

Δf(x) = Δx*y0 + ½Δx*Δy, или Δf(x) = ½Δx (y0 + y1);
Δf(y) = Δy*x0 + ½Δx*Δy, или Δf(y) = ½Δy (x0 + x1);
где x0, y0 – базисные (плановые) значения факторов, оказывающих влияние на результативный показатель; x1, y1 — фактические значения факторов; Δx = x1-x0, Δy = y1-y0 — абсолютные изменения (отклонения) факторов х, у соответственно;

Мультипликативная модель вида f = x*y*z:

Δf(x) = ½Δx (y0*z1 + y1*z0) + ⅓Δx*Δy*Δz;
Δf(y) = ½Δy (x0*z1 + x1*z0) + ⅓Δx*Δy*Δz;
Δf(z) = ½Δz (x0*y1 + x1*y0) + ⅓Δx*Δy*Δz;

Кратная модель вида f = x/y:

Δf(x) = Δx/Δy * ln |y1/y0|;
Δf(y) = Δf — Δf(x) = (f1-f0) — Δf(x);

Смешанная модель вида f = x/(y+z):

Δf(x) = Δx/(Δy+Δz) * ln |(y1+z1)/(y0+z0)|;
Δf(y) = (Δf — Δf(x))Δy / (Δy+Δz);
Δf(z) = (Δf — Δf(x))Δz / (Δy+Δz).

Пример применения интегрального способа для факторного анализа

Порядок применения интегрального способа рассмотрим на следующем примере. Проанализировать влияние на валовый объем производства количества работников и их выработки интегральным способом. Исходные данные представлены в таблице.

Показатель	Условное обозначение	Базисное значение (0)	Фактическое значение (1)	Изменение (+,-)
				Абсолютное	Относительное, %
Объем валовой продукции, тыс. руб.	ВП	2920	3400	+480	16,40
Среднесписочная численность персонала, чел.	ЧР	20	25	+5	25,00
Среднегодовая выработка продукции одним работником, тыс. руб.	ГВ	146	136	-10	-6,85

Решение. Зависимость объема производства продукции от данных факторов можно описать с помощью двухфакторной мультипликативной модели: ВП = ЧР * ГВ.

Алгоритм расчета влияния факторов интегральным способом таков:

• ΔВП(ЧР) = ΔЧР*ГВ0+½ΔЧР*ΔГВ = 5*146+0,5*5*(-10) = 705 тыс. руб. — влияние изменения численности персонала на объем производства;
• ΔВП(ГВ) = ΔГВ*ЧР0+½ΔЧР*Δ(-10) = -10*20+0,5*5*(-10) = -225 тыс. руб. — влияние изменения среднегодовой выработки продукции одним работником на объем производства;
• ΔВП = ΔВП(ЧР)+ ΔВП(ГВ) = 705 + (-225) = 480 тыс. руб. — суммарное влияние двух факторов.

Таким образом, использование интегрального метода знания основ интегрирования. Достаточно в готовые рабочие формулы подставить числовые данные и сделать расчеты.

Источник

Интегральный способ в экономическом анализе

Элиминирование имеет существенный недостаток. При его использовании исходят из того, что факторы изменяются независимо друг от друга. На самом деле они взаимосвязаны и в результате этого взаимодействия получает дополнительный прирост результат показателя, который при изменении способов элиминирования присоединяется к одному из факторов, как правило, к последнему. В связи с этим величина влияния факторов на результативный показатель меняется в зависимости от места, на которое поставлен тот или иной фактор в детерминированной модели. Интегральный метод частично компенсирует этот недостаток.

Формула интегрального метода для двухфакторной модели: у = а * b.

; , где
а = а1 – а0; b = b1 – b0
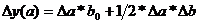
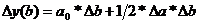
Для трехфакторной модели: у = а * b * с

После окончания расчетов надо
провести проверку
и сделать выводы.

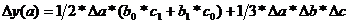
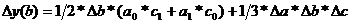
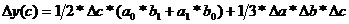
Источник

IX Международная студенческая научная конференция Студенческий научный форум — 2017

ИНТЕГРАЛЬНЫЙ МЕТОД В АНАЛИЗЕ ХОЗЯЙСТВЕННОЙ ДЕЯТЕЛЬНОСТИ

аддитивные модели (баланс товарной продукции);

мультипликативные модели (двухфакторная модель, выражающая зависимость между объемом выпуска продукции, количеством единиц оборудования и выработкой продукции в расчете на одну единицу оборудования);

кратные модели (формула, которая выражает зависимость между продолжительностью оборота оборотных активов в днях, средней величиной этих активов за данный период и однодневным объемом продаж);

смешанные модели (показатель рентабельности активов, на уровень которого влияют три фактора: чистая прибыль, величина внеоборотных активов, величина оборотных активов).

Вначале необходимо построить экономико-математическую модель, которая будет описывать влияние отдельных факторов на обобщающие экономические показатели деятельности организации. В анализе хозяйственной деятельности большое распространение получили многофакторные мультипликативные модели, именно они позволяют изучить влияние значительного количества факторов на обобщающие показатели. Это поможет достичь большей глубины и точности анализа.

После построения экономико-математической модели необходимо выбрать способ её решения. Есть ряд традиционных способов: цепных подстановок, балансовый, абсолютных и относительных границ, индексный метод, а также методы корреляционно-регрессионного, кластерного, дисперсионного анализа. Но наряду с ними в экономическом анализе используются и специфически математические методы и способы. Одним их таких методов является интегральный. Он направлен на определение влияния отдельных факторов с использованием мультипликативных, кратных кратно-аддитивных моделей.

При применении интегрального метода имеется возможность получить более обоснованные результаты исчисления влияния отдельных факторов, чем при использовании метода цепных подстановок и его вариантов. Эти методы имеют следующий ряд недостатков:

Результаты расчетов влияния факторов зависят от принятой последовательности замены базисных величин отдельных факторов на фактические величины;

Дополнительный прирост обобщающего показателя, вызванный взаимодействием факторов, в виде неразложимого остатка присоединяется к сумме влияния последнего фактора

Если же использовать интегральный метод, то прирост делится поровну между всеми факторами.Интегральный метод устанавливает общий подход к решению моделей различных видов, независимо от числа элементов, которые входят в данную модель, и формы связи между этими элементами.

В основе интегрального метода факторного анализа лежит суммирование приращений функций, определенной как частная производная, умноженная на приращение аргумента на бесконечно малых промежутках. При применении интегрального метода необходимо соблюдать следующие условия:

должно соблюдаться условие непрерывной дифференцируемости функции, где в качестве аргумента берется какой-либо экономический показатель;

функция между начальной и конечной точками элементарного периода должна изменяться по прямой;

должно иметь место постоянство соотношений скоростей изменения величин факторов

При использовании интегрального метода исчисления определенного интеграла по заданной подынтегральной функции и заданному интервалу интегрирования осуществляется по имеющейся стандартной программе с применением современных средств вычислительной техники.При осуществлении решения мультипликативной модели для расчета влияния отдельных факторов на обобщающий экономический показатель можно использовать следующие формулы:

При решении кратной модели для расчета влияния факторов воспользуемся формулами:

ΔZ(x) = Δx/Δy Ln y1/y0

Есть два основных типа задач, которые решаются при помощи интегрального метода: динамический и статистический. При статистическом отсутствует информация об изменении анализируемых факторов в течение данного периода. Примером такой задачи может быть анализ выполнения бизнес-планов либо анализ изменения экономических показателей по сравнению с предыдущим периодом. Динамический же тип задач имеет место в условиях наличия информации об изменении анализируемых факторов в течение данного периода. К такому типу задач можно отнести вычисления, связанные с изучением временных рядов экономических показателей.

Рассмотрим на примере преимущество интегрального метода.

Источник

Использование интегрального метода в экономике

Вы будете перенаправлены на Автор24

Понятие факторного анализа

Факторный анализ – это метод изучения взаимосвязей между переменными значениями.

Считается, что переменные, которые известны исследователю, находятся в зависимости от меньшего числа факторов и имеют меньшую тенденцию к проявлению ошибок. С помощью этого метода математического исследования можно решить две глобальных задачи:

1. Сформировать всестороннее описание объекта, а затем скомпоновать его.
2. Выявить скрытые факторы, которые влияют на линейную взаимосвязь изучаемых объектов и явлений.

Применение факторного анализа позволяет реализовать сразу несколько целей исследования. Прежде всего, он помогает установить взаимосвязи между переменными, а также сократить их число для описания зависимости. Для удобства схожие факторы группируют, что облегчает модель, а также делает ее более наглядной. При объединении факторов их влияние на объект будет выше, а значит, ярче проявятся свойства, связанные с его изменениями.

Группировка позволяет отследить скрытые факторы влияния. Это свойство особенно важно при исследовании социально-экономических явлений. Именно скрытые переменные, проявляющиеся в изменении объектов, называются факторами.

Чтобы определить наиболее значимые факторы применяются метод главных компонент. Его сущность заключается в замене взаимосвязанных величин не связанными между собой факторами. Для упрощения интерпретации результатов из уравнения могут исключаться менее информативные данные. Метод главных компонент является единственным математически обоснованным методом факторного анализа.

Факторный анализ имеет несколько форм. Он может быть разведочным, то есть направленным на выявление скрытых факторов. Конфирматорный анализ подтверждает гипотезы, относящиеся к исследованию числа факторов и оказываемых ими нагрузках.

Применение детерминированного факторного анализа в экономике

Факторный анализ широко применяется в экономических исследованиях, так как хозяйственные системы представляют собой динамические структуры, постоянно изменяющиеся под влиянием внутренних и внешних факторов. Для того, чтобы определить влияние фактора на структуру, а также выявить результат этого воздействия факторный анализ использует различные методы:

Готовые работы на аналогичную тему

1. Метод цепных подстановок.
2. Метод относительных и абсолютных разниц.
3. Метод баланса.
4. Метод индексов.
5. Логарифмический метод.
6. Интегральный метод.

Для того, чтобы исключить малозначимые факторы из уравнения наиболее часто используют метод цепных подстановок или абсолютных разниц. Первый метод предполагает подстановку в уравнение каждого фактора по очереди с целью определения его влияния на объект исследования. С помощью него можно определить степень влияния всех факторов, а затем исключить малозначимые. Для того, чтобы метод дал эффективный результат необходимо определить принципы последовательности подстановки. Метод абсолютных разниц используется в случае конкретизации абсолютных отклонений данных.

Метод индексов позволяет сопоставлять данные текущего и базисного периода. С его помощью можно проанализировать изменение данных с течением времени. Логарифмирование дает более высокую точность результатов исследования, так как влияние факторов распределяется на всю их совокупность.

Наиболее удобным методом является интегральный. Он помогает отследить влияние факторов как по отдельности, так и в совокупности. Так же с его помощью можно проанализировать количественные и качественные изменения. А общее влияние факторов распределяется на всю исследуемую совокупность.

Интегральный метод в экономике

Интегральный метод как бы обобщает метод цепных подстановок. Однако, его преимуществом является тот факт, что он не оказывает влияние на конечный результат исследования. Этот метод требует знаний в области математики, а также проведения большого числа вычислений, по сравнению с другими методами.

Элиминирование, которое часто применяется в факторном анализе, не учитывает взаимного влияния факторов друг на друга. Поэтому при его влиянии результат получает большее отклонение от реальной величины. Именно для того, чтобы избежать этого отклонения используется интегральный метод факторного анализа. В этом случае расположение факторов в модели не влияет на конечный результат исследовании. Кроме того, общий прирост результата под влиянием факторов распределяется в равных долях между всеми воздействующими переменными.

Чтобы повысить результативность анализа прирост рассматривается на отдельных временных промежутках, так как факторы могут иметь разную направленность воздействия. Таким образом, появляется возможность проанализировать приращение результата на малых временных отрезках. Итогом вычислений станет число, получаемого в результате суммирования результатов приращения.

Как правило, интегральный метод осуществляется с помощью вычислительной техники. От исследователя требует завести прединтегральные данные. Для практической деятельности часто применяют специальные рабочие формулы, которые позволяют учитывать факторную разнонаправленность. Эти данные приведены в специальной литературе, что очень облегчает процесс анализа. То есть, специалист подставляет в рабочие формулы фактические данные, а затем осуществляет расчеты. Таким образом, достигается наибольшая точность вычислений.

Интегральный метод не требует приемов, помогающих распределить неразложимый остаток, так как благодаря логарифмическому закону в нем автоматически осуществляется перераспределение факторов. С другой стороны, этот метод позволяет разложить показатель результата по факторам, что делает его универсальным в различных видах математических моделей.

Источник