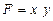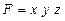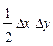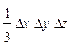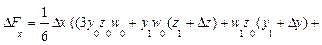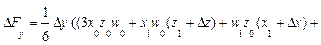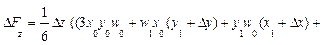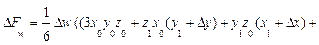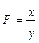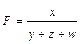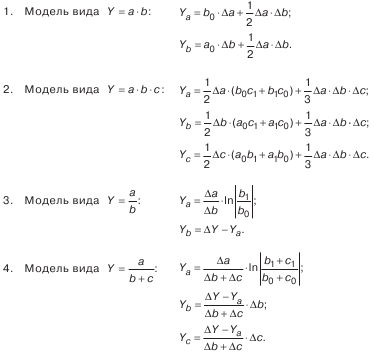Интегральный способ анализа влияния факторов

Интегральный способ детерминированного факторного анализа

Как известно, в детерминированном факторном анализе используют следующие основные способы:

• способ цепных подстановок;
• способ абсолютных разниц;
• способ относительных (процентных) разниц;
• интегральный метод и др.

Интегральный метод позволяет достигнуть полного разложения результативного показателя по факторам и носит универсальный характер – применяется для измерения влияния факторов в мультипликативных, кратных и смешанных моделях.

Использование этого способа позволяет получить более точные результаты по сравнению с остальными выше названными способами, поскольку дополнительный прирост результативного показателя от взаимодействия факторов присоединяется не к последнему фактору, а делится поровну между ними.

Рассмотрим алгоритмы расчетов влияния факторов для различных моделей, приводимые в специальной литературе:

Мультипликативная модель вида f = x*y:

Δf(x) = Δx*y0 + ½Δx*Δy, или Δf(x) = ½Δx (y0 + y1);
Δf(y) = Δy*x0 + ½Δx*Δy, или Δf(y) = ½Δy (x0 + x1);
где x0, y0 – базисные (плановые) значения факторов, оказывающих влияние на результативный показатель; x1, y1 — фактические значения факторов; Δx = x1-x0, Δy = y1-y0 — абсолютные изменения (отклонения) факторов х, у соответственно;

Мультипликативная модель вида f = x*y*z:

Δf(x) = ½Δx (y0*z1 + y1*z0) + ⅓Δx*Δy*Δz;
Δf(y) = ½Δy (x0*z1 + x1*z0) + ⅓Δx*Δy*Δz;
Δf(z) = ½Δz (x0*y1 + x1*y0) + ⅓Δx*Δy*Δz;

Кратная модель вида f = x/y:

Δf(x) = Δx/Δy * ln |y1/y0|;
Δf(y) = Δf — Δf(x) = (f1-f0) — Δf(x);

Смешанная модель вида f = x/(y+z):

Δf(x) = Δx/(Δy+Δz) * ln |(y1+z1)/(y0+z0)|;
Δf(y) = (Δf — Δf(x))Δy / (Δy+Δz);
Δf(z) = (Δf — Δf(x))Δz / (Δy+Δz).

Пример применения интегрального способа для факторного анализа

Порядок применения интегрального способа рассмотрим на следующем примере. Проанализировать влияние на валовый объем производства количества работников и их выработки интегральным способом. Исходные данные представлены в таблице.

Показатель	Условное обозначение	Базисное значение (0)	Фактическое значение (1)	Изменение (+,-)
				Абсолютное	Относительное, %
Объем валовой продукции, тыс. руб.	ВП	2920	3400	+480	16,40
Среднесписочная численность персонала, чел.	ЧР	20	25	+5	25,00
Среднегодовая выработка продукции одним работником, тыс. руб.	ГВ	146	136	-10	-6,85

Решение. Зависимость объема производства продукции от данных факторов можно описать с помощью двухфакторной мультипликативной модели: ВП = ЧР * ГВ.

Алгоритм расчета влияния факторов интегральным способом таков:

• ΔВП(ЧР) = ΔЧР*ГВ0+½ΔЧР*ΔГВ = 5*146+0,5*5*(-10) = 705 тыс. руб. — влияние изменения численности персонала на объем производства;
• ΔВП(ГВ) = ΔГВ*ЧР0+½ΔЧР*Δ(-10) = -10*20+0,5*5*(-10) = -225 тыс. руб. — влияние изменения среднегодовой выработки продукции одним работником на объем производства;
• ΔВП = ΔВП(ЧР)+ ΔВП(ГВ) = 705 + (-225) = 480 тыс. руб. — суммарное влияние двух факторов.

Таким образом, использование интегрального метода знания основ интегрирования. Достаточно в готовые рабочие формулы подставить числовые данные и сделать расчеты.

Источник

Интегральный метод

Интегральный метод применяется для измерения влияния факторов в мультипликативных, кратных и смешанных кратно-аддитивных моделях. Метод называется так потому, что для получения его формул использовалось интегральное исчисление. Самое важное, что следует знать об интегральном методе – это то, что он позволяет получать более точные результаты расчета влияния факторов по сравнению с методом цепных подстановок, индексным методом, методами абсолютных и относительных разниц, а также по сравнению с другими методами, которые мы называли в начале этой главы (кроме логарифмического метода). Причина в том, что в этих методах общее приращение результативного показателя представляется как сумма его приращений под влиянием изолированных друг от друга факторов. Например, если результирующий показатель F зависит от трех факторов: х, у и z, – то его приращение представляется как сумма трех приращений:

На самом же деле факторы действуют не изолированно, они взаимодействуют друг с другом и влияют на результирующий показатель совместно, из-за чего происходит дополнительный прирост результирующего показателя, который можно обозначить, как DF x, y, z , так что на самом деле приращение F представляет собой сумму четырех приращений:

По справедливости, приращение из-за взаимодействия факторов (DF x, y, z ) должно быть распределено между оценками влияния всех факторов (в данном примере между DF x ,DF y иDF z ). Но особенность формул МЦП, МАР, МОР и индексного метода в том, что это приращение не распределяется, а присоединяется к приросту результативного показателя под влиянием того фактора, который находится в модели на последнем месте (в данном примере – к величине DF z ). Соответственно, влияние последнего фактора завышается, а остальных – занижается. Таким образом, индексный метод, методы цепных подстановок, абсолютных и относительных разниц несут в себе погрешность, они дают неточные результаты. Кстати, из-за того, что величина DF x, y, z в этих методах не распределяется между оценками факторов, она была названа неразложимым остатком.

В интегральном методе эта неточность устраняется за счет того, что дополнительный прирост результативного показателя от взаимодействия факторов (неразложимый остаток) делится поровну между оценками влияния всех факторов (раскладывается). Из-за этого интегральный метод дает точные и единообразные результаты, которые не зависят от местоположения факторов в модели. Соответственно, при использовании интегрального метода для мультипликативных моделей не требуется предварительная классификация и расстановка факторов в определенном порядке.

Приведем формулы интегрального метода для мультипликативных моделей. Для двухфакторных моделей

формулы оценок влияния факторов выглядят следующим образом:

или ;

или .

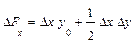
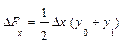
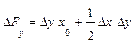
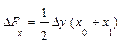
На примере этих формул становится понятно, почему интегральный метод дает единообразные результаты, которые не зависят от места факторов в модели. Формулы расчета оценок обоих факторов абсолютно идентичны. Если записать модель в виде:

,

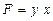
и, соответственно, заменить в формулах расчета оценок факторов х на у, а у – на х, то получим такие же две формулы, как исходные (и такие же результаты расчета по ним).

Для трехфакторных моделей

формулы имеют вид:

;

;

.

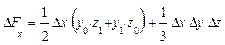
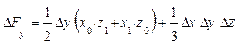
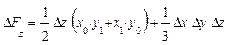
Обратим внимание читателей на последние слагаемые приведенных формул

в формулах для двухфакторной модели и

в формулах для трехфакторной модели. Эти слагаемые представляют собой неразложимый остаток, который разделен поровну, по числу факторов в этих моделях (соответственно, на 2 и 3 части) и присоединен равными частями к оценкам влияния каждого из факторов.

Приведем формулы интегрального метода для четырехфакторных моделей вида

:

;

;

;

.

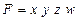
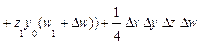
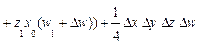
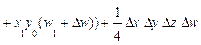
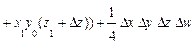
Как видим, в этих формулах неразложимый остаток разделен на четыре части и также поровну распределен между оценками влияния всех факторов.

Интегральный метод, в принципе, применим к мультипликативным моделям и с большим количеством факторов, но его формулы для таких моделей очень громоздки, и пользоваться ими для расчетов «вручную» слишком трудоемко.

Формулы интегрального метода для кратных моделей

; .

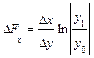
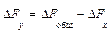
Прямые скобки означают, что выражение под знаком логарифма нужно брать по модулю.

Приведем формулы интегрального метода для смешанных моделей вида

.

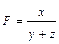
Эти формулы имеют вид:

;

; .

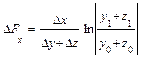
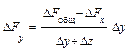
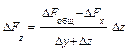
Для смешанных моделей вида

формулы интегрального метода – следующие:

;

;

; .

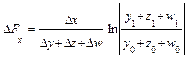
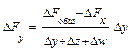
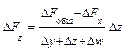
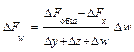
Как видим, использование интегрального метода не требует знания процесса интегрирования, его рабочие формулы требуют только знания арифметики и умения вычислять натуральные логарифмы (что несложно даже с помощью калькулятора). В конце решения прямой задачи факторного анализа интегральным методом, как и в остальных методах, требуется проверка в виде сложения оценок влияния всех факторов и сравнения этой суммы с общим приращением результирующего показателя.

Рассмотрим применение интегрального метода на данных примера 1 из пункта 5.3 (табл. 5.8).

Источник

11. Интегральный метод факторного анализа

11. Интегральный метод факторного анализа

Элиминирование как способ детерминированного факторного анализа имеет важный недостаток. При его использовании исходят из того, что факторы изменяются независимо друг от друга, однако фактически они изменяются взаимосвязанно, в результате образуется некоторый неразложимый остаток, который прибавляется к величине влияния одного из факторов (как правило, последнего). В связи с этим величина влияния факторов на изменение результативного показателя колеблется в зависимости от места фактора в детерминированной модели. Чтобы избавиться от этого недостатка, в детерминированном факторном анализе используется интегральный метод, который применяется для определения влияния факторов в мультипликативных, кратных и смешанных моделях кратно-аддитивного вида.

Использование этого способа позволяет получить более точные результаты вычисления влияния факторов по сравнению со способами цепной подстановки, абсолютных и относительных разниц и избежать неоднозначной оценки влияния: в данном случае результаты не зависят от местоположения факторов в модели, а дополнительный прирост результативного показателя, возникающий из-за взаимодействия факторов, распределяется между ними поровну.

Для распределения дополнительного прироста недостаточно взять его часть, соответствующую количеству факторов, т. к. факторы могут действовать в разных направлениях. Поэтому изменение результативного показателя измеряется на бесконечно малых отрезках времени, т. е. производится суммирование приращения результата, определяемого как частные произведения, умноженные на приращения факторов на бесконечно малых промежутках. Операция вычисления определенного интеграла решается с помощью ПЭВМ и сводится к построению подынтегральных выражений, которые зависят от вида функции или модели факторной системы. В связи со сложностью вычисления некоторых определенных интегралов и дополнительные сложностей, связанных с возможным действием факторов в противоположных направлениях, на практике используются специально сформированные рабочие формулы, приводимые в специальной литературе:

Таким образом, использование интегрального метода не нуждается в знании всего процесса интегрирования. Достаточно лишь в рабочие формулы подставить необходимые числовые данные и сделать подсчеты. При этом достигается более высокая точность расчетов.

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

Читайте также

3 Графический метод технического анализа

3 Графический метод технического анализа Любую тенденцию (тренд) можно разбить на составляющие ее более короткие тенденции. Компьютер сам строит для вас графики цены. Графики охватывают разные временные периоды. График часто называют чартом. Чарт – это график валютного

6.3. Применение метода коэффициентов для факторного анализа затрат по экономическим элементам

6.3. Применение метода коэффициентов для факторного анализа затрат по экономическим элементам Одним из важнейших приемов экономического анализа является сравнение показателей в динамике и статике. Для получения объективных результатов при использовании методического

9.6. Методика факторного анализа прибыли от продаж

9.6. Методика факторного анализа прибыли от продаж Прибыль от продаж – важнейшая составная часть прибыли до налогообложения.Прибыль от продаж зависит от трех основных факторов:1) от количества реализованной продукции по каждой позиции номенклатуры (ассортимента);2) от

10.2. Моделирование показателей рентабельности активов как база проведения факторного анализа

10.2. Моделирование показателей рентабельности активов как база проведения факторного анализа Экономико-математическое моделирование является основой методики факторного анализа.Модель рентабельности активов организации (Ra) может быть представлена в следующем виде

5. Метод и методика экономического анализа

5. Метод и методика экономического анализа Принципы метода экономического анализа: сравнение, детализация, элиминирование, использование объективный основ взаимосвязи экономических показателей.Методологическую основу экономического анализа предприятия

43. Коэффициентный метод как инструмент факторного анализа в оценке движения денежных средств

43. Коэффициентный метод как инструмент факторного анализа в оценке движения денежных средств Коэффициентный метод в анализе денежных потоков применяется для изучения уровней и их отклонения от плановых и базисных значений различных относительных показателей,

51. Метод и методика экономического анализа

51. Метод и методика экономического анализа Методологическую основу экономического анализа предприятия представляет моделирование характера взаимосвязи результативного показателя с показателями-факторами.Метод экономического анализа – это диалектический подход и

58. Метод функционально-стоимостного анализа

58. Метод функционально-стоимостного анализа Особое место в методах экономического анализа занимает метод функционально-стоимостного анализа (ФСА). Его чаще всего связывают с инженерным анализом – анализом научно-исследовательских и конструкторских разработок.

86. Факторный анализ и задачи прямого детерминированного факторного анализа

86. Факторный анализ и задачи прямого детерминированного факторного анализа Экономический факторный анализ – это постепенный переход от исходной факторной системы (результативный показатель) к конечной факторной системе (или наоборот), раскрытие полного набора прямых,

87. Задачи прямого стохастического факторного анализа

87. Задачи прямого стохастического факторного анализа Теперь рассмотрим особенности постановки задачи прямого стохастического факторного анализа. Если в случае прямого детерминированного факторного анализа исходные данные для анализа имеются в форме конкретных

88. Задачи обратного стохастического факторного анализа

88. Задачи обратного стохастического факторного анализа Задачи обратного факторного анализа могут быть детерминированными и стохастическими. Ее примерами являются задачи комплексной оценки производственно-хозяйственной деятельности, а также задачи математического

89. Модели детерминированного факторного анализа и аддитивные модели

89. Модели детерминированного факторного анализа и аддитивные модели Детерминированное моделирование факторных систем – простое и эффективное средство формализации связи экономических показателей. Оно служит основой для количественной оценки роли отдельных

91. Индексный метод, интегральный способ, метод цепных подстановок

91. Индексный метод, интегральный способ, метод цепных подстановок Индексный метод основан на построении факторных (агрегированных) индексов. Применение агрегированных индексов означает последовательное элиминирование влияния отдельных факторов на совокупный

96. Методы стохастического факторного анализа

96. Методы стохастического факторного анализа Самая общая и типичная статистическая задача в экономическом анализе – изучение наличия, направления и интенсивности связей между показателями . Это первый этап познания закономерностей формирования результатов

Метод функционального анализа

Метод функционального анализа Встретились два директора ткацких фабрик: русский и японец. Русский спрашивает: – Сколько человек работает на вашей фабрике? Японец отвечает: – Семь. Русский очень удивился, но виду не подал, решил не ударить в грязь лицом. Подумал, и

Вопрос 47 Методы факторного анализа прибыли от продажи

Вопрос 47 Методы факторного анализа прибыли от продажи Анализ прибыли от продажи проводится по трем направлениям: по каждому виду товара, по товарным группам и в целом по организации.На прибыль от продажи конкретного вида товара оказывают влияние объем продаж, цена

Источник