- Перемножение эпюр по правилу, методу или способу Мора-Верещагина: формула, таблица, примеры и задачи
- Верещагин и его метод, правило или способ
- Площадь и центр тяжести эпюр
- Перемножение эпюр по Верещагину
- Прямоугольник на прямоугольник
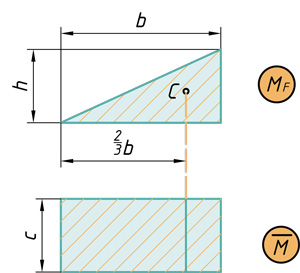
- Прямоугольник на треугольник
- Треугольник на прямоугольник
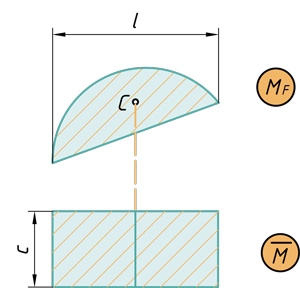
- Сегмент на прямоугольник
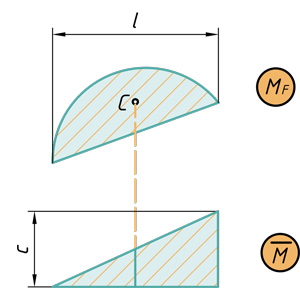
- Сегмент на треугольник
- Частные случаи расслоения эпюр на простые фигуры
- Прямоугольник и треугольник
- Два треугольника
- Два треугольника и сегмент
- Треугольник, прямоугольник и сегмент
- Пример определения перемещений: прогибов и углов поворотов по Верещагину
- Построение эпюры изгибающих моментов
- Построение единичных эпюр моментов
- Перемножение участков эпюры по Верещагину
- Определение прогиба сечения С
- Определение угла поворота сечения С
- Вычисление интегралов мора по способу верещагина
- Вычисление интегралов мора по способу верещагина
Перемножение эпюр по правилу, методу или способу Мора-Верещагина: формула, таблица, примеры и задачи
Привет! В этой статье будем учиться определять перемещения поперечных сечений при изгибе: прогибы и углы поворотов, по методу (способу, правилу) Верещагина. Причем, это правило широко используется не только при определении перемещений, но и при раскрытии статической неопределимости систем по методу сил. Я расскажу, о сути этого метода, как перемножаются эпюры различной сложности и когда выгодно пользоваться этим методом.
Верещагин и его метод, правило или способ
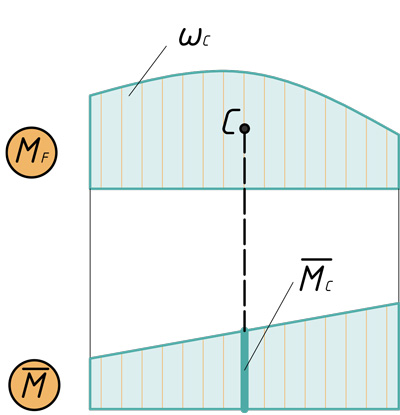
А.К. Верещагин в 1925г. предложил более простой способ решения (формулы) интеграла Мора. Он предложил вместо интегрирования двух функций перемножать эпюры: умножать площадь одной эпюры на ординату второй эпюры под центром тяжести первой. Этим способом можно пользоваться, когда одна из эпюр прямолинейна, вторая может быть любой. Кроме того, ордината берется прямолинейной эпюры. Когда эпюры обе прямолинейны, то тут совсем не важно, чью брать площадь, а чью ординату. Таким образом, эпюры по Верещагину перемножаются по следующей формуле:
Проиллюстрировано перемножение эпюр по Верещагину: C — центр тяжести первой эпюры, ωс — площадь первой эпюры, Mc — ордината второй эпюры под центром тяжести первой.
Площадь и центр тяжести эпюр
При использовании метода Верещагина, берется не сразу вся площадь эпюры, а частями, в пределах участков. Эпюра изгибающих моментов расслаивается на простейшие фигуры.
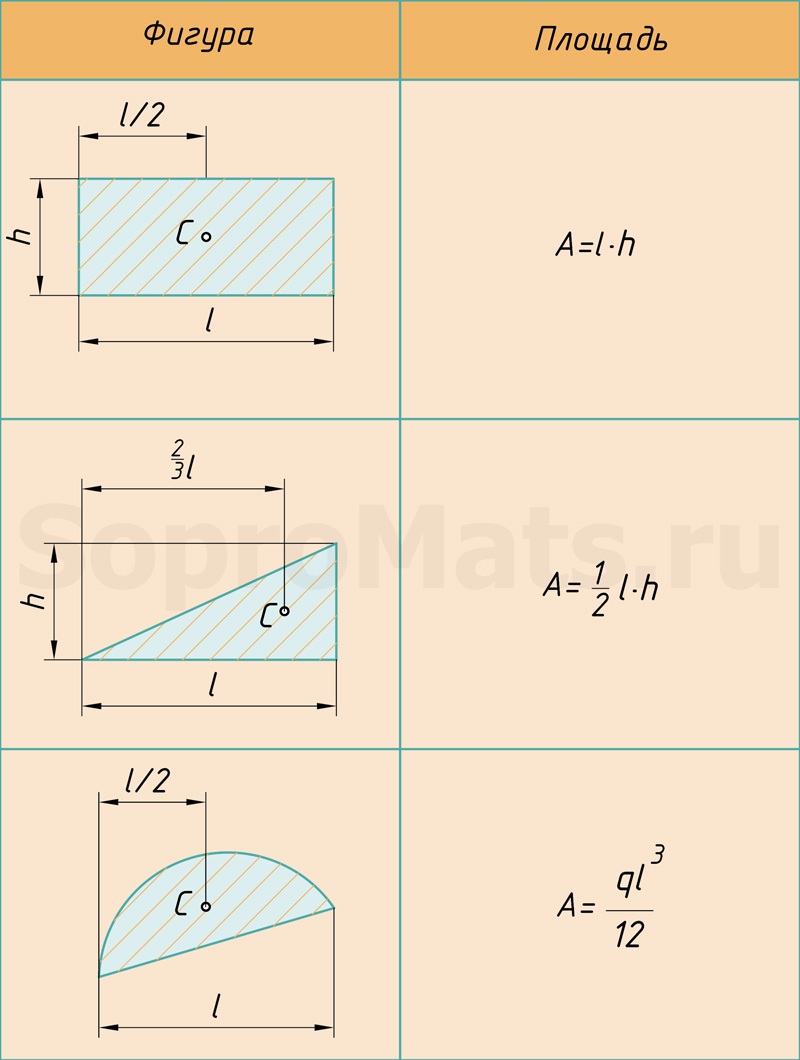
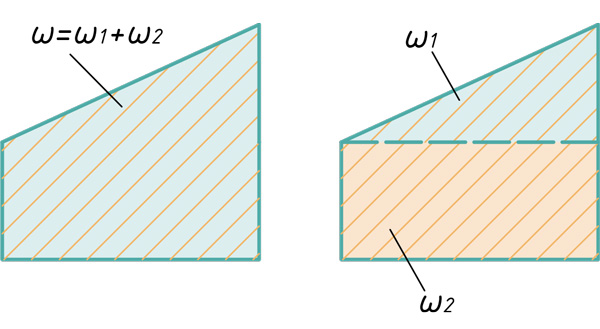
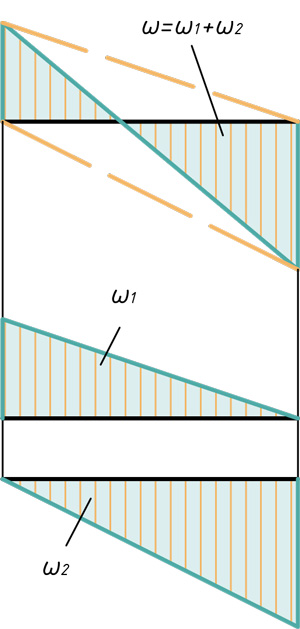
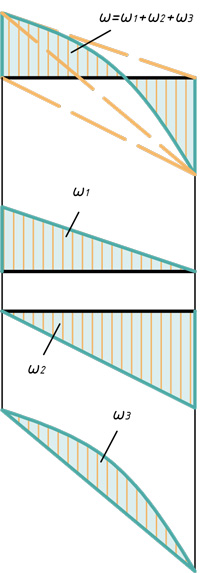
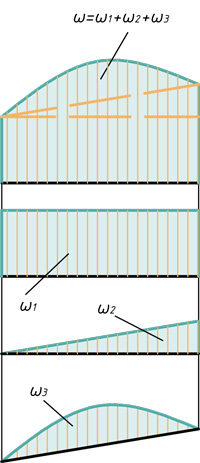
Любую эпюру можно расслоить всего на три фигуры: прямоугольник, прямоугольный треугольник и параболический сегмент.
Поэтому именно с этими фигурами будем дальше работать. Напомню, как вычислить их площадь и где у них находится центр тяжести. Все формулы и размеры оформил в виде таблицы:
Перемножение эпюр по Верещагину
В этом блоке статьи покажу частные случаи перемножения эпюр по Верещагину.
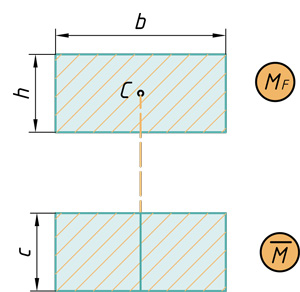
Прямоугольник на прямоугольник
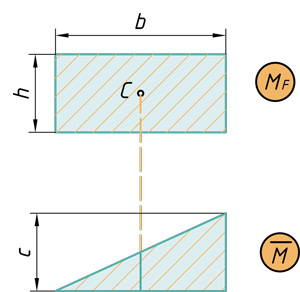
Прямоугольник на треугольник
Треугольник на прямоугольник
Сегмент на прямоугольник
Сегмент на треугольник
Частные случаи расслоения эпюр на простые фигуры
В этом блоке статьи покажу частные случаи расслоения эпюр на простые фигуры, для возможности их перемножения по Верещагину.
Прямоугольник и треугольник
Два треугольника
Два треугольника и сегмент
Треугольник, прямоугольник и сегмент
Пример определения перемещений: прогибов и углов поворотов по Верещагину
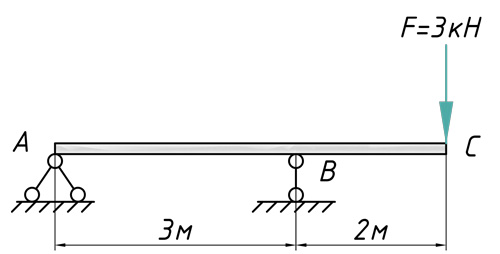
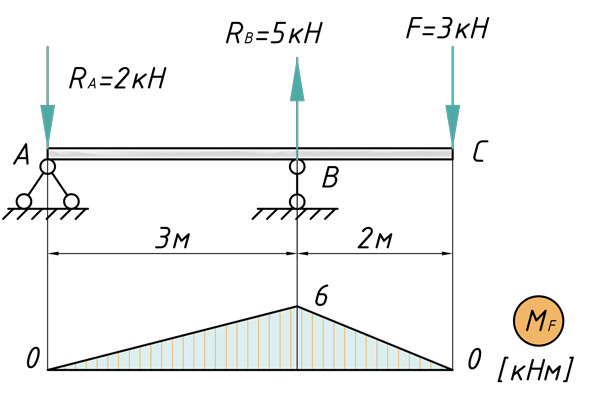
Теперь предлагаю рассмотреть конкретный пример с расчетом перемещений поперечных сечений: их прогибов и углов поворотов. Возьмем стальную балку, которая загружена всевозможными типами нагрузок и определим прогиб сечения C, а также угол поворота сечения A.
Построение эпюры изгибающих моментов
В первую очередь, рассчитываем и строим эпюру изгибающих моментов:
Построение единичных эпюр моментов
Теперь для каждого искомого перемещений необходимо приложить единичную нагрузку (безразмерную величину равную единице) и построить единичные эпюры:
- Для прогибов, прикладываются единичные силы.
- Для углов поворотов, прикладываются единичные моменты.
Например, после расчета величина прогиба получилась положительной, это значит, что направление перемещения сечения совпадает с направлением ранее прикладываемой силы. Тоже самое касается и углов поворотов.
Перемножение участков эпюры по Верещагину
После проведения всех подготовительных работ: построения эпюры изгибающих моментов, расслоения ее на элементарные фигуры и построения единичных эпюр от нагрузок, приложенных в местах и направлении искомых перемещений, можно переходить непосредственно к перемножению соответствующих эпюр.
Определение прогиба сечения С
Перемножаем соответствующие эпюры слева направо и вычисляем прогиб сечения C по методу Мора — Верещагина:
\[ < V >_< C >=\frac < 1 >< E< I >_ < x >> (\frac < 1 > < 2 >\cdot 6\cdot 3\cdot \frac < 2 > < 3 >\cdot 2+\frac < 1 > < 2 >\cdot 6\cdot 2\cdot \frac < 2 > < 3 >\cdot 2)=\frac < 20кН< м >^ < 3 >>< E< I >_ < x >> \]
Представим, что рассчитываемая балки имеет поперечное сечение в виде двутавра №24 по ГОСТ 8239-89, тогда прогиб балки будет равен:
Определение угла поворота сечения С
Перемножаем соответствующие эпюры слева направо и вычисляем угол поворота сечения C по правилу Мора — Верещагина:
Источник
Вычисление интегралов мора по способу верещагина




Вычисление интегралов мора по способу верещагина
- Расчет Интеграла по методу Мора Верещагина Если один из графиков (фактические состояния или единицы измерения) является прямой линией, вычисление интеграла моля значительно упрощается. Это условие, поскольку участок от одной нагрузки (концентрации или пары) всегда ограничен прямой линией, всегда выполняется для
системы, состоящей из прямых стержней. Вычислите Интеграл^M (A4pdx), если график от заданной нагрузки имеет произвольную форму и от единиц измерения — 380-прямая (рис. 377). Представляет площадь участка M g\s-его центроид, MS-вертикальная ось участка от единичной нагрузки под центроидом участка Mr Mpdx=dQ-дифференциальная область участка Mr, L4 Людмила Фирмаль
(13.59)представляет собой статический момент площади участка Mr для оси o-o: XdQ Дж. =х^г, / Где УГ-это абсцисса центра тяжести МР сюжет. В этом случае MtM Pdx = tg ahgy= = YL4G, (13.60) j Я Потому что… Таким образом, Интеграл Мора является свойством участка от внешней нагрузки в ординате линейного участка от единичной нагрузки, расположенной ниже центроида участка от заданной
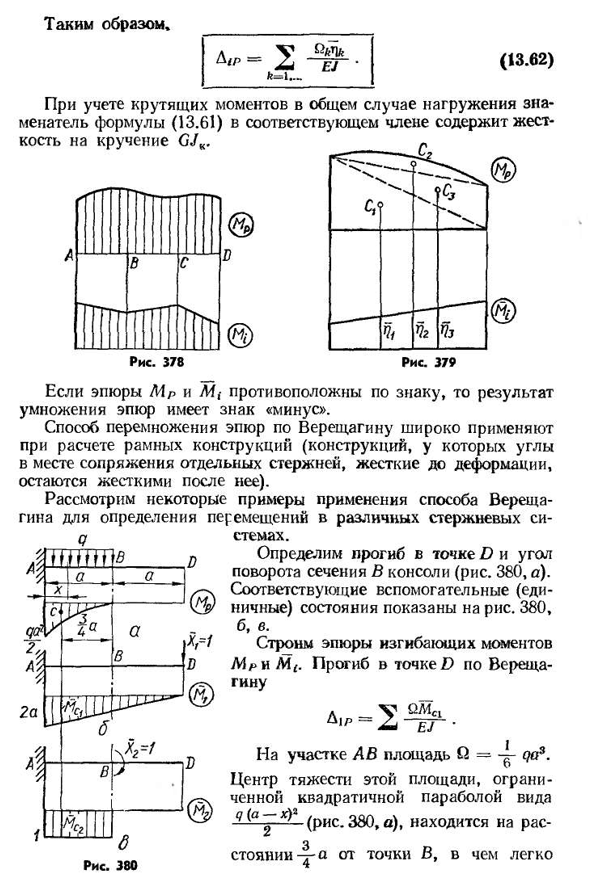
внешней нагрузки. Общая формула перемещения для системы линейных элементов (13.46) имеет вид (13.61) Описывается графоаналитический метод вычисления интеграла Mora. II. It предложен Верещагиным и называется методом Верещагина. Расчет по этой формуле проводится на каждом участке, где участок от единичной загрузки должен быть линейным(рис. 378). Если оба участка прямые, вы можете умножить любую область на ординату
- другой под первым центроидом. Если участок M R имеет сложную форму, то его следует разбить на простые фигуры(рис. 379), ибо легче определить площадь и расположение центра тяжести. В этом случае каждая область умножается на ординату единичного участка, которая находится ниже центроида соответствующей области. В этом случае удобно указать вместо символа MEK G)L, k-1;2;… 3s1 следующим образом* (13.62) Рассматривая крутящий момент в общем случае нагрузки, знаменатель уравнения соответствующего члена (13.61) содержит жесткость на кручение GJ Если участок Mr противоположе
н знаку, то результат умножения участка имеет знак минус. Метод умножения участка Верещагина широко используется при расчете каркасной конструкции (угол на границе раздела отдельных стержней, жесткость до деформации, затем остается жесткой). В данной работе рассматривается применение метода Верещагина для определения перемещений в различных стержневых системах. Определите отклонение точки D и угол поворота сечения в консоли (рис. 380, а). Соответствующее вспомогательное (единичное) состояние показано на рисунке. 380, Б, В. Изгибающий момент в точке D по Верещагину строит диаграмму прогиба m pH m s Площадь участка равна(2=qa3.
Центр тяжести этой области окружен вторичной параболой вида (рис. 380, а) находится Людмила Фирмаль
на расстоянии — ^ — от точки в, в чем легко убедиться, применив формулу (2.3). Вертикальная ось вспомогательного участка L4c1=a. BD Q=0 на сайте. Итак, qa *
EG Для определения угла поворота вспомогательная система загружается одной парой. Очевидно, MS2-1. Следовательно, угол поворота секции л У1 2P-EJ
SEJ • Триста восемьдесят один рис Определим полное перемещение точек из кадра, показанного на рисунке. 381, и, предполагая EJ=const. A = вычислить вертикальное и горизонтальное смещения данной точки для определения полного смещения ПЗС. Для определения вертикального перемещения точки с Рама во вспомогательном состоянии нагружается силой x=1, направленной вертикально(рис. 381, б). Основной сюжет Mr показан на рисунке. 381, g, aux Mi-на фиг. 381, д.,
Расчет производится на сайте: SV site Й, = Т; ; Для управления АВ О2 = МХ\й=/. И так оно и есть., Для определения горизонтального перемещения вспомогательной системы горизонтальная сила x2=1(Рис. 381, в). Участок м2 показан на рисунке. 381, е. 383evidentally SV vertical on the site=0, а AV на сайте Vertical t) 2= » gr., Но __Mh2^2Р»
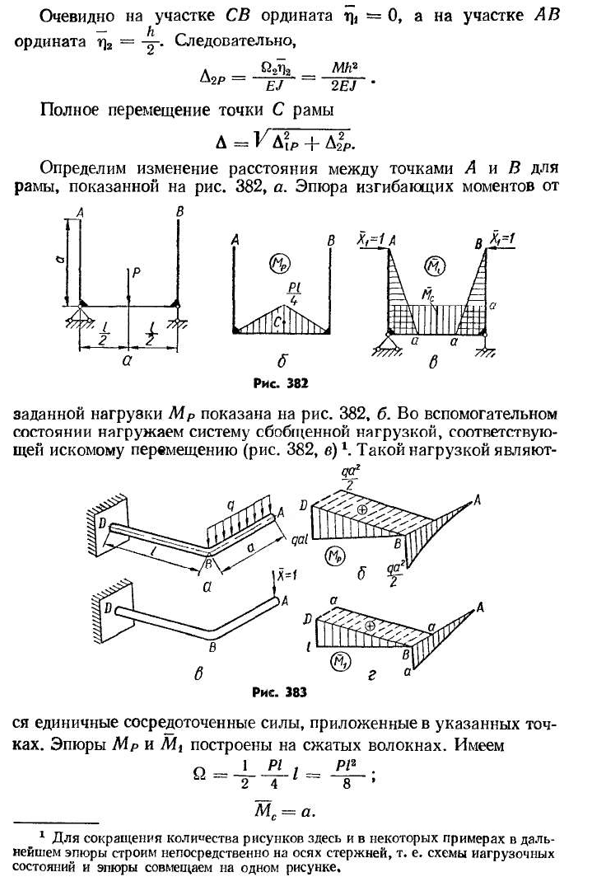
2е Г’ Идеальное смещение пятна от рамки A=D(R+DGR Попробуем определить изменение расстояния между точками кадров, показанных на рисунке. 382, a. график изгиба a и B на мгновение из Данная нагрузка M P показана на рисунке. 382, b.
In вспомогательное состояние, нагружающее систему обобщенной нагрузкой, соответствующей требуемому перемещению (фиг. 382, Б) 1. Такие нагрузки бывают Это единственные силы концентрации, которые действуют в этих точках. Участки Mr и Mi были построены на сжатом волокне. Иметь
8′ _________MS=а. Чтобы уменьшить число фигур 1, в некоторых будущих примерах участок строится непосредственно на оси стержня. 384 противоречия, Но L/R QMC RRA EJ8EJ — Определим падение сломанного консольного свободного конца круглого сечения, нагруженного в сечение АВ вертикальной равномерной распределенной нагрузкой(рис. 383, а).
Диаграммы изгиба и крутящего момента основного и вспомогательного состояний показаны на рисунке. 383, Б, г. График крутящего момента размещен на горизонтальной плоскости, его координаты представлены пунктирной линией.: Лл / ρ=>1Т^3Т г+,-Y1T1?Л г/2; Т2(т+





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Источник