Информатика числовой способ кодирования

Кодирование числовой информации

Вы будете перенаправлены на Автор24

Десятичное и двоичное представление чисел

Для работы с числовой информацией мы пользуемся системой счисления, содержащей десять цифр: от $0$ до $9$. Эта система называется десятичной.

Кроме цифр, в десятичной системе большое значение имеют разряды. Подсчитывая количество чего-нибудь и дойдя до самой большой из доступных нам цифр (до $9$), мы вводим второй разряд и дальше каждое последующее число формируем из двух цифр. Дойдя до $99$, мы вынуждены вводить третий разряд. В пределах трех разрядов мы можем досчитать уже до $999$ и т.д.

Таким образом, используя всего десять цифр и вводя дополнительные разряды, мы можем записывать и проводить математические операции с любыми, даже самыми большими числами.

Компьютер ведет подсчет аналогичным образом, но имеет в своем распоряжении всего две цифры — логический ноль (отсутствие у бита какого-то свойства) и логическую единицу (наличие у бита этого свойства).

Система счисления, использующая только две цифры, называется двоичной. При подсчете в двоичной системе добавлять каждый следующий разряд приходится гораздо чаще, чем в десятичной.

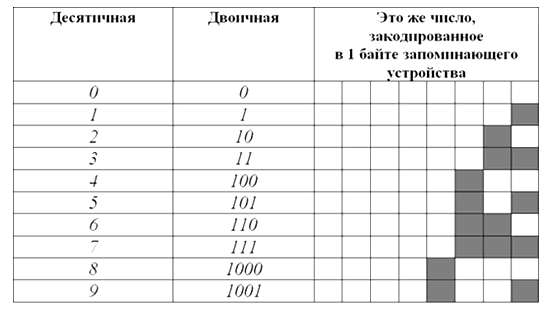
Вот таблица первых десяти чисел в каждой из этих систем счисления:

Как видите, в десятичной системе счисления для отображения любой из первых десяти цифр достаточно $1$ разряда. В двоичной системе для тех же целей потребуется уже $4$ разряда.

Готовые работы на аналогичную тему

Соответственно, для кодирования этой же информации в виде двоичного кода нужен носитель емкостью как минимум $4$ бита ($0,5$ байта). Человеческий мозг, привыкший к десятичной системе счисления, плохо воспринимает систему двоичную. Хотя обе они построены на одинаковых принципах и отличаются лишь количеством используемых цифр. В двоичной системе точно так же можно осуществлять любые арифметические операции с любыми числами. Главный ее минус — необходимость иметь дело с большим количеством разрядов.

Так, самое большое десятичное число, которое можно отобразить в 8 разрядах двоичной системы — $255$, в $16$ разрядах – $65535$, в $24$ разрядах – $16777215$.

Алгоритмы кодирования чисел в двоичной системе счисления

Компьютер, кодируя числа в двоичный код, основывается на двоичной системе счисления. Но, в зависимости от особенностей чисел, может использовать разные алгоритмы:

Небольшие целые числа без знака.

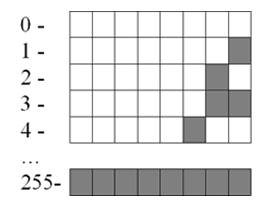
Для сохранения каждого такого числа на запоминающем устройстве, как правило, выделяется $1$ байт ($8$ битов). Запись осуществляется в полной аналогии с двоичной системой счисления.

Целые десятичные числа без знака, сохраненные на носителе в двоичном коде, будут выглядеть примерно так:

Большие целые числа и числа со знаком.

Для записи каждого такого числа на запоминающем устройстве, как правило, отводится $2$-байтний блок ($16$ битов).

Старший бит блока (тот, что крайний слева) отводится под запись знака числа и в кодировании самого числа не участвует. Если число со знаком «плюс», этот бит остается пустым, если со знаком «минус» – в него записывается логическая единица. Число же кодируется в оставшихся 15 битах. Например, алгоритм кодирования числа $+2676$ будет следующим:

• Перевести число $2676$ из десятичной системы счисления в двоичную. В итоге получится $101001110100$;
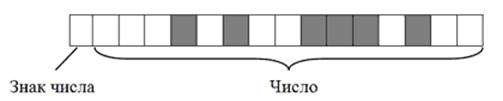
• Записать полученное двоичное число в первые $15$ бит $16$-битного блока (начиная с правого края). Последний, $16$-й бит, должен остаться пустым, поскольку кодируемое число имеет знак $+$.

В итоге $+2676$ в двоичном коде на запоминающем устройстве будет выглядеть так:

Примечательно, что в двоичном коде присвоение числу отрицательного значения предусматривает не только изменение старшего бита. Осуществляется также инвертирование всех остальных его битов.

Чтобы было понятно, рассмотрим алгоритм кодирования числа $-2676$:

1. Перевести число $2676$ из десятичной системы счисления в двоичную. Получим все тоже двоичное число $101001110100$;
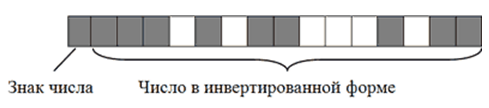
2. Записать полученное двоичное число в первые $15$ бит $16$-битного блока. Затем инвертировать, то есть, изменить на противоположное, значение каждого из $15$ битов;
3. Записать в $16$-й бит логическую единицу, поскольку кодируемое число имеет отрицательное значение.

В итоге $-2676$ на запоминающем устройстве в двоичном коде будет иметь следующий вид:

Запись отрицательных чисел в инвертированной форме позволяет заменить все операции вычитания, в которых они участвуют, операциями сложения. Это необходимо для нормальной работы компьютерного процессора.

Максимальным десятичным числом, которое можно закодировать в $15$ битах запоминающего устройства, является $32767$. Иногда для записи чисел по этому алгоритму выделяются $4$-байтные блоки. В таком случае для кодирования каждого числа будет использоваться $31$ бит плюс $1$ бит для кодирования знака числа. Тогда максимальным десятичным числом, сохраняемым в каждую ячейку, будет $2147483647$ (со знаком плюс или минус).

Дробные числа со знаком.

Дробные числа на запоминающем устройстве в двоичном коде кодируются в виде так называемых чисел с плавающей запятой (точкой). Алгоритм их кодирования сложнее, чем рассмотренные выше. Тем не менее, попытаемся разобраться.

Для записи каждого числа с плавающей запятой компьютер чаще всего выделяет $4$-байтную ячейку ($32$ бита):

• в старшем бите этой ячейки (тот, что крайний слева) записывается знак числа. Если число отрицательное, в этот бит записывается логическая единица, если оно со знаком «плюс» – бит остается пустым.
• во втором слева бите аналогичным образом записывается знак порядка (что такое порядок поймете позже);
• в следующих за ним $7$ битах записывается значение порядка.
• в оставшихся $23$ битах записывается так называемая мантисса числа.

Чтобы стало понятно, что такое порядок, мантисса и зачем они нужны, переведем в двоичный код десятичное число $6,25$.

Порядок кодирования будет примерно следующим:

1. Перевести десятичное число в двоичное (десятичное $6,25$ равно двоичному $110,01$);
2. Определить мантиссу числа. Для этого в числе необходимо передвинуть запятую в нужном направлении, чтобы слева от нее не осталось ни одной единицы. В нашем случае запятую придется передвинуть на три знака влево. В итоге, получим мантиссу, $11001$;
3. Определить значение и знак порядка. Значение порядка – это количество символов, на которое была сдвинута запятая для получения мантиссы. В нашем случае оно равно $3$ (или $11$ в двоичной форме);

Знак порядка – это направление, в котором пришлось двигать запятую: влево – «плюс», вправо – «минус». В нашем примере запятая двигалась влево, поэтому знак порядка – «плюс».

Таким образом, порядок двоичного числа $110,01$ будет равен $+11$, а его мантисса, $11001$. В результате в двоичном коде на запоминающем устройстве это число будет записано следующим образом

Обратите внимание, что мантисса в двоичном коде записывается, начиная с первого после запятой знака, а сама запятая упускается. Числа с плавающей запятой, кодируемые в $32$ битах, называю числами одинарной точности. Когда для записи числа $32$-битной ячейки недостаточно, компьютер может использовать ячейку из $64$ битов. Число с плавающей запятой, закодированное в такой ячейке, называется числом двойной точности.

Источник

Кодирование числовой информации

Введение

Если у вас возникли какие-либо вопросы при изучении темы «Кодирование числовой информации», то звоните мне и записывайтесь на первый репетиторский урок по информатике и ИКТ. На моих индивидуальных уроках мы с вами закроем текущие пробелы в ваших знаниях и прорешаем колоссальное количество всевозможных тематических упражнений.

Общие понятие о числовой информации

Думаю, что превалирующее число школьников и студентов знает фразу: «Математика – царица всех наук!». А как известно, математика очень интенсивно оперирует числами, цифрами и действиями над числами.

Первый счет появился много тысячелетий назад, так как даже в очень древние времена люди столкнулись с потребностью в счете. Его возникновение связано с желанием человека проинформировать своих соплеменников о количестве обнаруженных им объектов, предметов. По началу люди просто делили предметы по принципу один-много. То есть не было обозначения для двух, трех, десяти и более различных предметов. Их просто обозначали в количественном отношении как много.

Постепенно люди научились подключать к арифметическому счету пальцы на своих руках. С их помощью можно было считать до пяти, а если использовать обе руки, то до десяти различных предметов. Именно десятичная система счисления получило свое развитие на основе использования при счете пальцев рук.

Вернемся в настоящий временной континуум. Для современного человека знания, позволяющие считать предметы и записывать числа, являются обязательными. Арифметика изучается в школе с первого класса. Цифры, используя которые мы записываем числа, называются арабскими. Алфавит арабских цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Всего десять различных цифр или состояний.

Числа можно классифицировать на две фундаментальные группы:

Дробные или действительные числа.

Каждое число из представленных групп может быть либо:

Примеры различных десятичных чисел:

-56 — целое отрицательное число;

12.78 — действительное положительное число;

0.0 — действительное число, равное нулю;

12000 — целое положительное число.

Наша цель – понять, каким образом производится кодирование числовой информации, выраженной целыми или дробными числами, которые являются положительными, отрицательными или равными нулю. Другими словами, мы должны понять, как персональный компьютер хранит, обрабатывает, копирует числа на «своем» уровне.

Свойства числовой информации

Конечность. Информация, выраженная числовым значением, должна быть конечной. Процессор персонального компьютера не сможет обработать число, которое не является конечным или завершенным. То есть прежде чем приступить к кодированию числовой информации, процессор должен быть уверен, что данное значение записано полностью и не будет изменено пользователем.

Понятность. Если мы говорим о кодировании числовой информации, которая представлена десятичным числом, то необходимо, чтобы само число состояло из элементов, которые будут понятны исполнителю при кодировании. Исполнителем является, в строгом приближении, процессор персонального компьютера. Например, число 129 состоит из трех цифр: 1, 2 и 9. Каждое из этих цифр входит в состав арабского алфавита. Если мы представим числовую информацию в виде значения 89J1’4, то подобное значение будет некорректно обработано процессором и он выдаст исключение, то есть сгенерирует ошибку. Почему? Потому что входное число 89J1’4 состоит из элементов: 8, 9, J, 1, ‘, 4, не каждое из которых входит в состав арабского алфавита. Например, элементы J и ‘ не являются арабскими цифрами.

Приведенные два свойства являются ключевыми в алгоритмах кодирования числовой информации. Пожалуй, еще стоит отметить неосновное свойство – размер числа. Но в современном мире мощности персональных компьютеров постоянно увеличиваются и самые эффективные процессоры способы обрабатывать огромные значения.

Способы кодирования числовой информации

Сразу необходимо твердо уяснить следующее: процессор персонального компьютера взаимодействует с любыми данными исключительно на уровне цепочек, состоящих из 0 и 1. Набор нулей и единиц называют двоичным или бинарным кодом. То есть любые текстовые, символьные или числовые значения, которые понятны простому человеку, процессор преобразует в двоичный код. Следовательно, наша задача – научиться переводить числовые значения в бинарное представление, состоящее из цепочек 0 и 1.

Для полного осознания алгоритма кодирования числовой информации необходимо очень хорошо уяснить понятие «Машинное слово». Возможно вы слышали, что иногда пользователи говорят, что на их компьютерах установлена 32-х разрядная или 64-х разрядная система Microsoft Windows. Именно значение разрядности (в приведенном примере это 32 или 64) и отвечает за то, сколько бит информации будет выделено для хранения какого-либо математического значения при кодировании числовой информации. То есть, если нам дано положительное целое число 25, то при преобразовании его в бинарный код, ему будет выделено 32 или 64 бита. Также напомню, что один байт информации состоит из 8 битов.

Далее по тексту я буду работать на уровне 16-и разрядной системы. То есть любое кодирование числовой информации будет представлено с использованием машинного слова в 16 бит.

Кодирование целых положительных чисел

Это наиболее простой способ кодирования данных, так как для его реализации необходимо уметь переводить числа из десятичной системы счисления в двоичную систему. Ниже я приведу таблицу, в которой покажу кодирование целых положительных чисел различной значности.

Исходное десятичное число

Закодированное десятичное число в двоичном коде

Источник

Информатика

Именная карта банка для детей
с крутым дизайном, +200 бонусов

Закажи свою собственную карту банка и получи бонусы

План урока:

Примеры кодирования информации:

• трансляция письменных сообщений с использованием русских букв (АБВГД…ЭЮЯ);
• запись чисел цифрами (0123456789);
• использование языка жестов при общении глухонемых людей

Другими словами, переход сообщения из одной формы ее в другую, согласно определенным правилам, и выражает в чем суть кодирования информации.

Информация проходит кодирование в целях:

• упрощения сбора исходных данных;
• сокращения объема занимаемой памяти информационными сообщениями;
• удобства хранения материалов;
• эффективной обработки и обмена информацией;
• сокрытия необходимых сведений.

История кодирования информации насчитывает сотни веков. Издавна люди использовали криптограммы (зашифрованные сообщения).

В 19 веке с изобретением телеграфа С. Морзе был придуман и принципиально новый способ шифрования. Телеграфное сообщение передавалось по проводам последовательностью коротких и долгих сигналов (точка и тире).

Вслед за ним Ж. Бодо создал основополагающий в истории современной информатики метод бинарного кодирования информации, который заключается в применении всего двух различающихся электрических сигналов. Кодирование информации в компьютере также подразумевает использование двух чисел.

Разработанная в 1948г. К. Шенноном «Теория информации и кодирования» стала основополагающей в современном кодировании данных.

Кодирование информации в информатике, одна из базовых тем. Понимание для чего нужна процедура кодирования передаваемой информации, каким образом она осуществляется, поможет в изучении принципов работы компьютера.

Способы кодировки

Проанализируем разнообразные виды информации и особенности ее кодирования.

По принципу представления все информационные сведения можно классифицировать на следующие группы:

• графическая;
• аудиоинформация (звуковая);
• символьная (текстовая);
• числовая;
• видеоинформация.

Способы кодирования информации обусловлены поставленными целями, а также имеющимися возможностями,методами ее дальнейшей обработки и сохранения. Одинаковые сообщения могут отображаться в виде картинок и условных знаков (графический способ), чисел (числовой способ) или символов (символьный способ).

Соответственно происходит и классификация информации по способу кодирования:

• символьные сообщения включают знаки дорожного движения, сигналы светофора и т.д.;
• текстовые данные – это книги, нотные записи, различные документы;
• всевозможные изображения (фотографии, схемы, рисунки) представляют все многообразие графической информации.

Чтобы расшифровать сообщение, отображаемое в выбранной системе кодирования информации, необходимо осуществить декодирование – процесс восстановления до исходного материала. Для успешного осуществления расшифровки необходимо знать вид кода и методы шифрования.

Самыми распространенными видами кодировок информации являются следующие:

• преобразование текста;
• графическая кодировка;
• кодирование числовых данных;
• перевод звука в бинарную последовательность чисел;
• видеокодирование.

Различают такие методы кодирования информации как:

• метод замены (подстановки) – знаки первоначального сообщения заменяются на соответствующие символы выбранного кодового алгоритма;
• метод перестановки – символы оригинального текста меняются местами по определенной схеме;
• метод гаммирования – к исходным обозначениям добавляется случайная последовательность других знаков.

Двоичный код

Самый широко используемый метод кодирования информации – двоичное кодирование. Кодирование данных двоичным кодом применяется во всех современных технологиях.

Двоичный (бинарный) код — последовательность нолей и единиц. Это универсальный способ отображения любых информационных сведений (текстовых сообщений, картинок, звуковых и видеоматериалов). Сведения, закодированные в бинарном коде, очень удобно хранить, обрабатывать и передавать с одного электронного устройства на другое, в чем и заключается преимущества использования двоичного кодирования информации.

Двоичное кодирование информации применяется для различных данных:

• двоичное кодирование текстовой информации заключается в присвоении буквенным, цифровым и другим обозначениям определенного кода. Он записывается в компьютерной памяти цепочкой из нулей и единиц. Порядок кодирования алфавита в двоичный код с помощью стандарта ASCII является наглядным примером;
• вид используемой графики влияет на то, каким образом производится двоичное кодирование графической информации;
• двоичное кодирование звуковой информации происходит после дискретизации звуковой волны и присвоения каждому компоненту соответствующего бинарной цепочки чисел;
• кодирование двоичным кодом видеоматериалов сочетает принципы работы со звуком и растровыми изображениями.

Обработка графических изображений

Кодирование текстовой, звуковой и графической информации осуществляется в целях ее качественного обмена, редактирования и хранения. Кодировка информационных сообщений различного типа обладает своими отличительными чертами, но, в целом, она сводится к преобразованию их в двоичном виде.

Рисунки, иллюстрации в книгах, схемы, чертежи и т.п. – примеры графических сообщений. Современные люди для работы с графическими данными все чаще применяют компьютерные технологии.

Суть кодирования графической и звуковой информации заключается в преобразовании ее из аналогового вида в цифровой.

Кодирование графической информации – это процедура присвоения каждому компоненту изображения определенного кодового значения.

Способы кодирования графической информации подчиняются методам представления изображений (растрового или векторного):

1. Принцип кодирования графической информации растровым способом заключается в присвоении бинарного шифра пикселям (точкам), формирующим изображение. Код содержит сведения о цветовых оттенках каждой точки. Примером служат снимки, сделанные на цифровом фотоаппарате.

1. Векторная кодировка осуществляется благодаря использованию математических функций. Компонентам векторных изображений (точкам, прямым и другим геометрическим фигурам) присваивается двоичная последовательность, определяющая разнообразные параметры. Такая графика зачастую применяется в типографии.

Источник

Многим станет интересно: «В чем суть кодирования графической информации, представленной в виде 3D-изображений?» Дело в том, что работа с трехмерными данными сочетает способы растровой и векторной кодировки.

Кодирование и обработка графической информации различного формата имеет как свои преимущества, так и недостатки.

Метод координат

Любые данные можно передать с помощью двоичных чисел, в том числе и графические изображение, представляющие собой совокупность точек. Чтобы установить соответствие чисел и точек в бинарном коде, используют метод координат.

Метод координат на плоскости основан на изучении свойств точки в системе координат с горизонтальной осью Ox и вертикальной осью Oy. Точка будет иметь 2 координаты.

Если через начало координат проходит 3 взаимно перпендикулярные оси X, Y и Z, то используется метод координат в пространстве. Положение точки в таком случае определяется тремя координатами.

Система координат в пространстве

Перевод чисел в бинарный код

Числовой способ кодирования информации, т.е. переход информационных данных в бинарную последовательность чисел широко распространен в современной компьютерной технике. Любая числовую, символьную, графическую, аудио- и видеоинформацию можно закодировать двоичными числами. Рассмотрим подробнее кодирование числовой информации.

Привычная человеку система счисления (основанная на цифрах от 0 до 9), которой мы активно пользуемся, появилась несколько сотен тысяч лет назад. Работа всей вычислительной техники организована на бинарной системе счисления. Алфавитом у нее минимальный – 0 и 1. Кодировка чисел совершается путем перехода из десятичной в двоичную систему счисления и выполнении вычислений непосредственно с бинарными числами.

Кодирование и обработка числовой информации обусловлено желаемым результатом работы с цифрами. Так, если число вводится в рамках текстового файла, то оно будет иметь код символа, взятого из используемого стандарта. Для математических вычислений числовые данные преобразуются совершенно другим способом.

Принципы кодирования числовой информации, представленной в виде целых или дробных чисел (положительных, отрицательных или равных 0) отличаются по своей сути. Самый простой способ перевести целое число из десятичной в двоичную систему счисления заключается в следующем:

1. число нужно разделить на 2;
2. если частное больше 1, то необходимо продолжить деление до того момента, пока результат будет равен 0 или 1;
3. записать результат последней операции и остатки от деления в обратной последовательности;
4. полученное число и будет являться искомым кодовым значением.

Одна из важнейших частей компьютерной работы – кодирование символьной информации. Все многообразие цифр, русских и латинских букв, знаков препинания, математических знаков и отдельных специальных обозначений относятся к символам. Cимвольный способ кодирования состоит в присвоении определенному знаку установленного шифра.

Рассмотрим подробнее самые распространенные стандарты ASCII и Unicode – то, что применяется для кодирования символьной информации во всем мире.

Фрагмент таблицы ASCII

Первоначально было установлено, что для любого знака отводится в памяти компьютера 8 бит (1 бит – это либо «0», либо «1») бинарной последовательности. Первая таблица кодировки ASCII (переводится как «американский кодовый стандарт обмена сообщениями») содержала 256 символов. Ограниченная численность закодированных знаков, затрудняющая межнациональный обмен данными, привела к необходимости создания стандарта Unicode, основанного на ASCII. Эта международная система кодировки содержит 65536 символов. Закодировать огромное количество всевозможных обозначений стало возможным благодаря использованию 16-битного символьного кодирования.

Кодирование символьной и числовой информации принципиально отличается. Для ввода-вывода цифр на монитор или использовании их в текстовом файле происходит преобразование их согласно системе кодировки. В процессе арифметических действий число имеет совершенно другое бинарное значение, потому что оно переходит в двоичную систему счисления, где и совершаются все вычислительные действия.

Выбирать способ кодирования информации – графический, числовой или символьный необходимо отталкиваясь от цели кодировки. Например, число «21» можно ввести в компьютерную память цифрами или буквами «двадцать один», слово «ЗИМА» можно передать русскими буквами «зима» или латинскими «ZIMA», штрих-код товара передается изображением и цифрами.

Преобразование звука

Компьютерные технологии успешно внедряются в различные сферы деятельности, включая кодирование и обработку звуковой информации. С физической точки зрения, звук – это аналоговый сплошной сигнал. Процесс его перевода в ряд электрических импульсов называется кодированием звуковой информации.

Задачи, которые необходимо решить для успешной оцифровки сигнала:

1. дискретизировать (разделить аудиоданные на элементарные участки путем измерения колебаний воздуха через одинаковые интервалы времени);
2. оцифровать (присвоить каждому элементу числовой код).

Преобразование звука: а) аналоговый сигнал; б)дискретный сигнал.

Различают следующие методы кодирования звуковой информации:

• Метод FM. Суть его сводится к разделению звука аналого-цифровыми преобразователями (АЦП) на одинаковые простейшие элементы, которые в дальнейшем кодируются бинарным кодом. Несовершенство метода FM проявляется в низком качестве звукозаписи из-за потери некоторого объема исходного звукового сообщения.
• Метод Wave-Table (таблично-волновой) позволяет получить высококачественный продукт, поскольку разработанные таблицы сэмплов (образцов «живых» звуков) позволяют выразить бинарными числами разнообразные параметры поступающего сигнала.

Обработка текста

Текст – осмысленный порядок знаков. С использованием компьютера кодирование и обработка текстовой информации (набор, редактирование, обмен и сохранение письменного текста) значительно упростилось.

Кодирование текстовой информации – присвоение любому символу текста кода из кодировочной системы. Различают следующие стандарты кодировки:

1. ASCII – первая международная система кодировки, содержащая коды на 256 знаков.
2. Unicode – расширенный стандарт ASCII, превышающий ее размером в 256 раз.
3. КОИ-8, СР1251, СР866, ISO – русские таблицы кодировки букв. При этом следует понимать, что документ, закодированный одним стандартом, не будет читаться в другом.

В задачах на кодирование текстовой информации часто встречаются следующие понятия:

• мощность алфавита;
• единицы измерения памяти (биты и байты).

Например, мощность алфавита ASCII составляет 256 символов. При этом один знак занимает 8 бит (или 1 байт) памяти, а Unicode – 35536 символов и 16 бит (или 2 байта) соответственно.

Источник