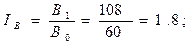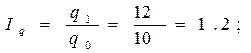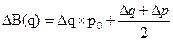Индексный способ факторного анализа это

Индексный метод факторного анализа

Для оценки количественной роли отдельных факторов часто используется индексный метод.

Индексы –это относительные величины, характеризующие соотношение величин во времени. Индекс рассчитывается как отношение фактического показателя к базовому. Индексы применяются для характеристики динамики показателей, а также оценки влияния отдельных факторов на результативный показатель. Индексный метод применяется при наличии двух факторов и мультипликативной связи между ними.

В нашем примере изменение объема выпуска продукции рассматривается в связи с изменением численности работающих и их производительности труда:

In = (Ч1 * ПТ1) / (Ч0 * ПТ0)

Где: In – индекс изменения объема продукции; Iч – индекс изменения численности работающих; Iпт – индекс изменения производительности труда.

Взаимосвязь показателей можно представить индексной системой:

Изменение объема выпуска продукции за определенный период может быть выражено как результат влияния двух факторов: изменения производительности труда по каждому виду продукции и численности работников, занятых выпуском продукции соответствующего вида:

IN = (∑Пт1 * Ч1) / (∑Пто * Чо) = ((∑Пто*Ч1) / (∑Пто*Чо)) * ((∑Пт1*Ч1) / (∑Пт0*Ч1) = Iч * Iпт

где: Iч — индекс численности работающих; Iпт — индекс производительности труда.

Индекс численности работающих, отражающий влияние на изменение объема продукции численности работающих рассчитывается:

Iч = ∑ПТ1*Ч1 / ∑ПТ1*Ч0

Индекс производительности труда, который отражает влияние на изменение объема продукции изменения производительности труда рассчитывается:

I пт =∑ПТ1*Ч1 /∑ПТ0*Ч1

А разница между суммой в числителе и знаменателе показывает абсолютное значение влияния факторов.

На основе следующих данных (таблица № 2) дать оценку влияния факторов на изменение объема продукции.

Показатели	Базисный период		Отчетный период
	А	В	А	В
Продукция,т.р.	24 000	10 000	27 000	9 120
Численность работников	300	50	290	48
Производительность труда т.р./чел.	80	200	93,1	190

Для того, чтобы оценить влияние изменения численности и производительности труда на изменение объема продукции:

1) вычисляем индекс численности работников:

Iч = (93,1*290 + 190*48) / (93,1*300 + 190*50) = 36119 / 37430 = 0,96

2) вычисляем индекс производительности труда:

Iпт = (93,1*290 + 190*48) / (80*290 + 200*48) = 36119/32800 = 1,1

3) Индекс изменения объема продукции:

In = Iт * Iп = 0,96 * 1,1 = 1,06

In = N1 /N0 = (27000+9120) / (24000 + 10000) = 1,06

Источник

Индексный метод в факторном анализе

В статистике, планировании и анализе хозяйственной деятельности основой для количественной оценки роли отдельных факторов в динамике изменений обобщающих показателей являются индексные модели. Индексный метод – один из приемов элиминирования. Основывается на относительных показателях динамики, пространственных сравнений, выполнении плана, выражающих отношение фактического уровня анализируемого показателя в отчетном периоде к его уровню в базисном периоде (или к плановому, или по другому объекту). Любой индекс исчисляется сопоставлением соизмеряемой (отчетной) величины с базисной. Индексы, выражающие соотношение непосредственно соизмеряемых величин, называются индивидуальными, а характеризующие соотношения сложных явлений – групповыми, или тотальными.

Статистика оперирует различными формами индексов (агрегатная, арифметическая, гармоническая и др.), используемыми в аналитической работе.

Агрегатный индекс является основной формой любого общего индекса; его можно преобразовать как в средний арифметический, так и в средний гармонический индексы. С помощью агрегатных индексов можно выявить влияние различных факторов на изменение уровня результативных показателей в мультипликативных и кратных моделях.

Корректность определения размера каждого фактора зависит от:

1. количества знаков после запятой (не менее четырех);
2. количества самих факторов (связь обратно пропорциональна).

Принципы построения индексов: изменение одного фактора при неизменном значении всех остальных, при этом если обобщающий экономический показатель представляет собой произведение количественного (объемного) и качественного показателей-факторов, то при определении влияния количественного фактора качественный показатель фиксируется на базисном уровне, а при определении влияния качественного фактора количественный показатель фиксируется на уровне отчетного периода.

Пусть Y = а*b*с*d. Тогда:

При этом: I Y=I a*I b*I c*I d.

Индексный метод позволяет провести разложение по факторам не только относительных, но и абсолютных отклонений обобщающего показателя. В этом случае влияние отдельных факторов определяется с помощью разности между числителем и знаменателем соответствующих индексов, т. е. также при расчете влияния одного фактора элиминируется влияние другого:

Пусть Y = а*b, где а – количественный фактор, a b – качественный. Тогда:

a 1*b 0—a 0*b 0– абсолютный прирост результирующего показателя за счет фактора а;

a 1*b 1—a 1*b 0– абсолютный прирост результирующего показателя за счет фактора b;

a 1*b 1—a 0*b 0– абсолютный прирост результирующего показателя за счет влияния всех факторов.

Данный принцип разложения абсолютного прироста (отклонения) обобщающего показателя по факторам пригоден для случая, когда число факторов равно двум (один из них количественный, другой – качественный), а анализируемый показатель представлен как их произведение.

Теория индексов не дает общего метода разложения абсолютных отклонений обобщающего показателя по факторам при числе факторов более двух. Для решения этой задачи используется метод цепных подстановок.

Источник

Индексный метод факторного анализа

Сущность индексного метода факторного анализа состоит в сле­дующем: во-первых, определяются индекс результативного показате­ля и индексы факторов; во-вторых, устанавливается схема взаимосвя­зи индекса результативного показателя с индексами факторов; в-тре­тьих, составляется алгоритм расчетов влияния факторов на изменение результативного показателя.

Рассмотрим применение индексного метода факторного анализа на примере. Имеем информацию о выручке от продаж в торговой точке за два аналогичных периода времени.

B₀ =10 тыс. шт. х 6 руб. = 60 тыс. руб.

В₁ = 12 тыс. шт. х 9 руб. = 108 тыс. руб.

ΔВ = В₁ — В_о = 108 — 60 = +48 тыс. руб.

Рассчитаем индексы результативного показателя и индексы фак­торов:

Взаимосвязь индекса результативного показателя с индексами факторов аналогична взаимосвязи самого результативного показате­ля с факторами, т.е.

Алгоритм I расчетов влияния факторов индексным методом

1) влияние на выручку изменения количества проданного товара

3) влияние на выручку изменения цены единицы товара

Проверка: ΔВ = В₁ — В_о = ΔВ (q) + ΔВ(р).

Расчеты влияния факторов:

1) ΔВ (q) = (1,2- 1,0) х 60 тыс. руб. = +12 тыс. руб.;

2) ΔВ (р) = (1,2 х 1,5- 1,2) х 60 тыс. руб. = +36 тыс. руб.

Проверка: ΔВ = 108 — 60 = 12 + 36, или

48 тыс. руб. = 48 тыс. руб.

Достоинство индексного метода состоит в том, что изменение результативного показателя раскладывается по факторам без остат­ка. Вместе с тем этому методу свойственен серьезный недостаток — элемент субъективизма. Он заключается в произвольном определе­нии порядка расположения факторов в цепочке сомножителей.

Рассмотренный выше алгоритм соответствует только одному ва­рианту расположения факторов, т.е.

С позиций математики равноправным является и другой вариант расположения факторов, т.е.

Однако второму варианту расположения факторов соответству­ют другой алгоритм и другие результаты расчетов.

Алгоритм, 2 расчетов влияния факторов индексным методом

1) влияние на выручку изменения цены единицы товара

2) влияние на выручку изменения количества проданного товара

Проверка: ΔВ = В₁ — В_о = ΔВ (р) + ΔВ (q).

Расчеты влияния факторов:

1) ΔВ (р) = (1,5 — 1,0) х 60 тыс. руб. = +30 тыс. руб.;

2) ΔВ (q) = (1,5 х 1,2 — 1,5) х 60 тыс. руб. = +18 тыс. руб.

Проверка: ДВ = 108 — 60 = 30 + 18, или 48 тыс. руб. = 48 тыс. руб.

Таким образом, результаты расчетов влияния факторов по двум вариантам не совпадают. Причиной несовпадения является «неразложенный остаток». В первом варианте он «присоединился» к фактору «изменение цены единицы товара». Во втором — к фактору «измене­ние количества проданного товара».

С увеличением числа факторов-сомножителей резко возрастает количество равноправных вариантов расчетов, так как увеличивается число возможных перестановок факторов. Например, число переста­новок из трех по три равно шести, из четырех по четыре — 24, а из пяти по пять — 120.

Для обоснования правильности только одного из многих вариан­тов экономисты вывели следующее правило индексного метода фак­торного анализа. Все факторы можно разделить на две группы:

1)количественные (первичные, или экстенсивные);

2)качественные (вторичные, или интенсивные).

При расстановке факторов в модели исходят из следующего: на первое место ставится количественный фактор, на второе — каче­ственный. В соответствии с этим положением следует признать пра­вильным первый из рассмотренных нами алгоритмов. Вместе с тем необходимо помнить, что данное правило субъективно.

Для лучшего понимания сущности индексного метода приведем алгоритм расчетов для решения трехфакторной мультипликативной модели.

расчетов влияния факторов индексным методом для решения трехфакторной мультипликативной модели

Расчеты влияния факторов:

Метод цепных подстановок

Метод цепных подстановок является производным от индексно­го метода факторного анализа. Его суть состоит в следующем. Для расчета влияния факторов на изменение результативного показате­ля определяется условная величина (подстановка), отражающая, каков был бы результативный показатель, если бы один фактор изме­нился, а другие остались бы неизменными.

Если в модели число факторов-сомножителей более двух, то при­ходится определять несколько взаимосвязанных подстановок (це­почку подстановок). Отсюда название — метод цепных подстано­вок.

Алгоритм 1 расчетов влияния факторов методом цепных подстановок

Сумма влияния двух факторов равняется изменению результатив­ного показателя:

Расчеты влияния факторов:

1)влияние на выручку изменения количества проданного товара
ΔВ(q) = (12 — 10) тыс. шт. х 6 руб. = +12 тыс. руб;

2)влияние на выручку изменения цены единицы товара
ΔВ(р) = (9 — 6) тыс. шт. х 12 руб. = +36 тыс. руб.

Проверка: Δ В = 108 — 60 = 12 + 36, или 48 тыс. руб. = 48 тыс. руб.

Достоинство метода цепных подстановок, как и индексного метода, состоит в том, что изменение результативного показателя расклады­вается по факторам без остатка. Вместе с тем методу цепных подста­новок присущ элемент субъективизма, который заключается в выборе порядка расположения факторов в цепочке сомножителей.

Рассмотренный выше алгоритм соответствует только одному ва­рианту расположения факторов, т.е.

С позиций математического подхода равноправным является и другой вариант расположения факторов, т.е.

Однако второму варианту расположения факторов соответству­ют другой алгоритм и другие результаты расчетов.

Алгоритм 2 расчетов влияния факторов методом цепных подстановок

Расчеты влияния факторов:

1) влияние на выручку изменения цены единицы товара
ΔВ(р) = (9 — 6) тыс. шт. х 10 руб. = +30 тыс. руб.;

2) влияние на выручку изменения количества проданного товара
ΔВ(q) = (12 — 10) тыс. шт. х 9 руб. = +18 тыс. руб.

Проверка: ΔВ = 108-60 = 30+ 18, или 48 тыс. руб. = 48 тыс. руб.

Для обоснования правильности одного из многих вариантов эко­номисты вывели следующее субъективное правило метода цепных подстановок. Влияние изменения на результативный показатель коли­чественного фактора подсчитывается при базовом значении качествен­ного фактора, т.е.

Влияние изменения на результативный показатель качественного фактора определяется при отчетном значении количественного фак­тора, т.е.

С позиций данного правила следует признать обоснованным пер­вый из двух рассмотренных алгоритмов. Вместе с тем нужно по­мнить, что это правило субъективно.

Для более полной иллюстрации сущности метода цепных под­становок приведем алгоритм расчетов влияния факторов на ре­зультативный показатель для трехфакторной мультипликативной модели.

Алгоритм расчетов влияния факторов методом цепных подстановок для решения трехфакторной мультипликативной модели

Расчеты влияния факторов:

При практическом применении цепных подстановок возникли раз­личные модификации этого метода, предназначенные для упрощения расчетов, — способ абсолютных отклонений, способ относительных отклонений, способ процентных разниц.

3.8. Интегральный метод факторного анализа

Интегральный метод факторного анализа применяется в ,тех случаях, когда результативный показатель может быть представлен как функция от нескольких аргументов. Изменения функции в зави­симости от изменения аргументов описываются соответствующими интегральными выражениями.

При проведении факторного анализа интегральный метод может быть использован для решения двух типов задач [5].

К первому типу относятся такие задачи, в которых отсутствует информация об изменении факторов внутри анализируемого периода либо от этого изменения можно абстрагироваться. В данном случае величина изменения результативного показателя не зависит от порядка расположения факторов в модели. Этот тип задач называется статическим. В качестве примера можно привести сравнительный анализ показателей двух аналогичных объектов.

Второй тип задач связан с анализом показателей в динамике, т.е. когда имеются данные об изменении факторов внутри анализиру­емого периода.

Интегральный метод факторного анализа дает общий подход к решению задач разного типа независимо от количества факторов, вхо­дящих в модель, схемы взаимосвязи между ними и порядка расположе­ния факторов в модели. Этот метод позволяет осуществить расчеты влияния факторов на результативный показатель в мультипликатив­ных, кратных и смешанных моделях без образования «неразложенного остатка».

Применение интегрального метода дает возможность получить од­нозначные результаты расчетов влияния факторов на изменение ре­зультативного показателя.

При использовании интегрального метода изменение выручки от продаж можно представить как сумму двух интегралов. Один из них характеризует зависимость выручки от количества проданного това­ра, а другой — от цены единицы товара.

расчетов влияния факторов интегральным методом для решения двухфакторной мультипликативной модели

Δ В = В₁-В₀=

где f'(q), f'(p) — функции изменения выручки в зависимости соот­ветственно от количества проданного товара и цены его единицы.

Исходя из предположения, что данные факторы в пределах не­большого промежутка времени изменяются по линейному закону, расчеты влияния факторов на изменение выручки можно предста­вить следующим образом:

1) влияние изменения количества проданного товара

3) влияние изменения цены единицы товара

Однако интегральный метод также имеет существенный недоста­ток: с увеличением в модели числа факторов-сомножителей резко повышается сложность вычислений, т.е. возрастают объем и трудоем­кость расчетов влияния каждого фактора на изменение результатив­ного показателя.

Рассмотрим алгоритм расчетов влияния факторов интегральным методом для решения трехфакторной мультипликативной модели.

расчетов влияния факторов интегральным методом для решения трехфакторной мультипликативной модели

В практике аналитической работы интегральный метод не получил широкого распространения. Он используется преимущественно в на­учно-исследовательских разработках в области экономического ана­лиза.

Источник