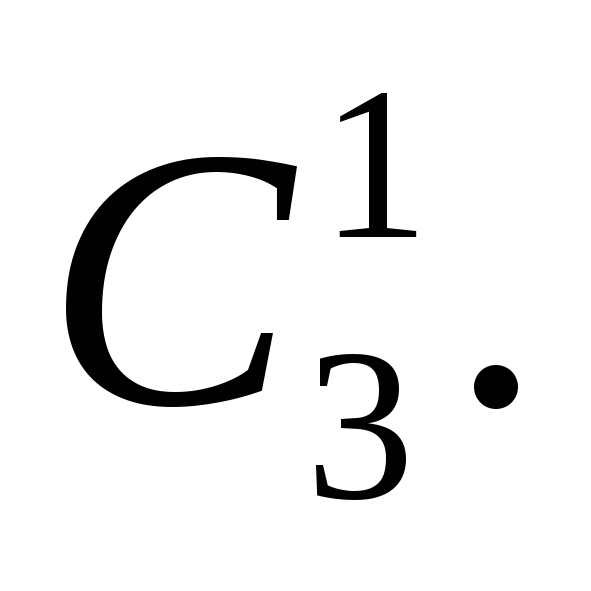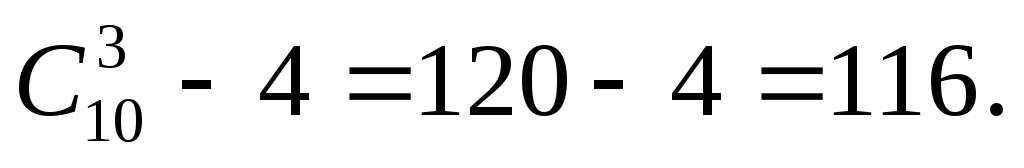Имеется 6 пар перчаток различных размеров сколькими способами можно выбрать

Сколькими способами из шести пар перчаток различных размеров можно выбрать одну перчатку на левую руку и одну

Сколькими способами можно обменять одну книгу одного на одну книгу другого
У одного человека есть 7 книг по математике, а у другого — 9 книг. Сколькими способами можно.

Сколькими способами можно построить их в одну шеренгу?
Приветствую, :friends: В классе 12 девочек и 10 мальчиков. Сколькими способами можно .

Сколькими способами можно обменять одну книгу?
Доброго времени суток. Имеется такая задача: У одного студента 7 книг, у другого 9 разных книг.

Решение

Сколькими способами можно сложить все коробки в одну
Даны 6 коробок разных размеров, причём в любую коробку умещается сколько угодно коробок меньших.

Сколькими способами можно выбрать комиссию в составе 5-ти человек из 6-ти пар братьев и сестер
Сколькими способами можно выбрать комиссию в составе 5-ти человек из 6-ти пар братьев и сестер так.

Сколькими способами можно выбрать трёх кроликов различных цветов?
Здравствуйте! Не могу понять, как решить задачу: «Сколькими способами можно выбрать трёх кроликов.

Сколькими способами можно выбрать три различных числа из множества?
Сколькими способами можно выбрать три различных из множества <1,2, . 100>так, чтобы их сумма.

Источник

Контрольная работа № 00 по предмету «Высшая математика» часть 2 (код-вш)

1. Из города а в город в ведут 5 дорог, из города в в город с — три дороги. Сколько путей, проходящих через в, ведут из а в с?

Представим задачу в виде графа, см. рис. 1.

Рис. 1. Граф путей, связывающих пункты А, В и С.

Очевидно, что какой бы путь не выбрал объект, продвигаясь из пункта А в пункт В, по достижении пункта В он может выбрать любой из трех путей, позволяющих ему добраться из В в С.

Следовательно, путей, ведущих из А в С и проходящих через В, существует 5  3 = 15.

2. Имеется 6 пар перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую руку и одну — на правую так, чтобы выбранные перчатки были разных размеров?

На левую руку можно выбрать любую из 6 перчаток на левые руки. На правую – любую из пяти перчаток на правую руку. Значит, всего способов

3. Пять девушек и трое юношей играют в городки. Сколькими способами они могут разбиться на две команды по 4 человека, если в каждой команде должно быть хотя было одному юноше?

По условию задачи, в одной команде должен быть 1 юноша, а в другой 2.

Сформировать команды при таких условиях можно следующим образом.

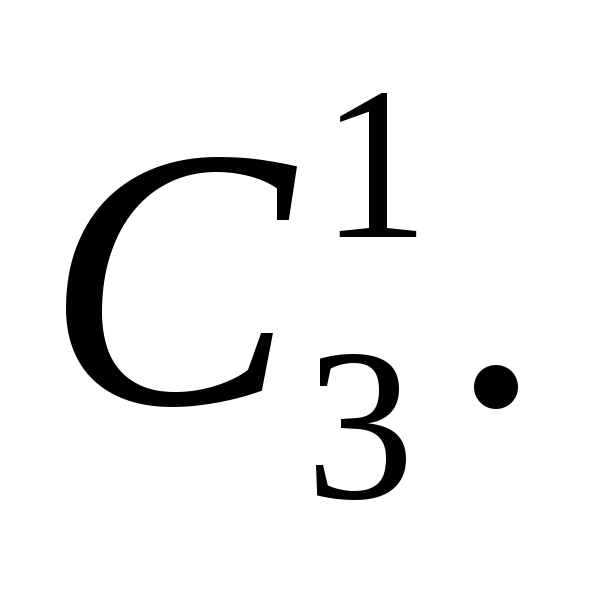
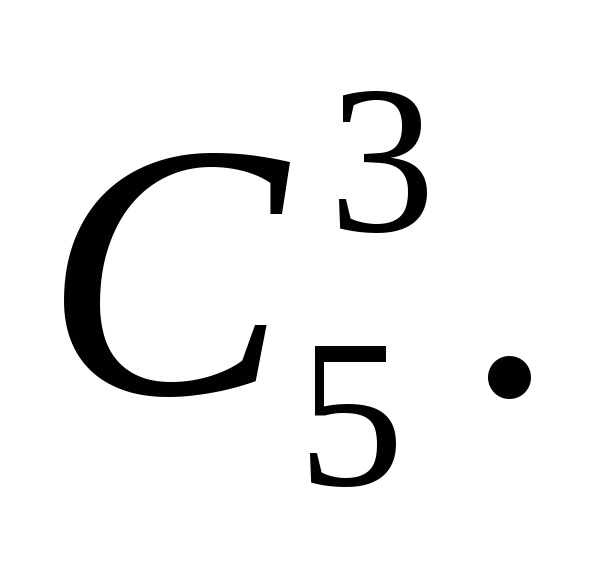
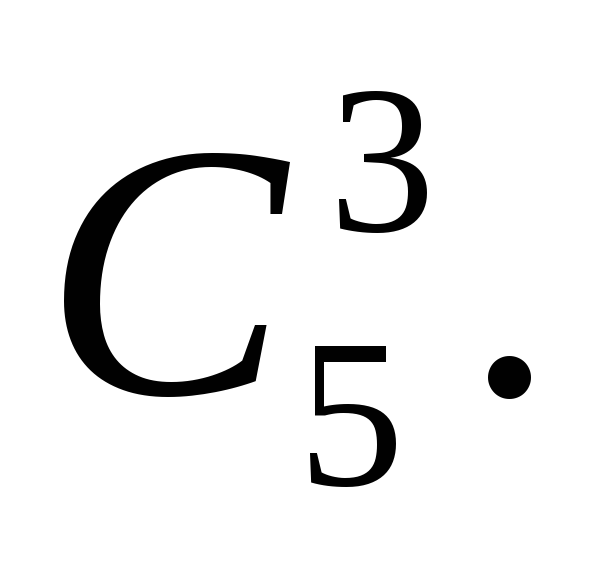
Юношу в первую команду можно выбрать способами, выбрать девушек в эту команду можно способами. Оставшиеся 2 юношей и 2 девушки составят другую команду. Значит, всего имеется =30 способов разбиться на команды.

4. В купе железнодорожного вагона имеются два противоположных дивана по 5 мест на каждом. Из 10 пассажиров этого купе четверо желают сидеть лицом к паровозу, 3 – спиной к паровозу, а остальным безразлично как сидеть. Сколькими способами могут разместиться пассажиры с учетом их желаний?

Разместим четверых желающих пассажиров лицом к паровозу (на 5 местах). Это можно сделать способами, разместим троих желающих пассажиров спиной к паровозу. Это можно сделать способами, Осталось 3 «безразличных» пассажира и для них 3 места. Их можно разместить 3! способами.

Значит, всего способов размещения .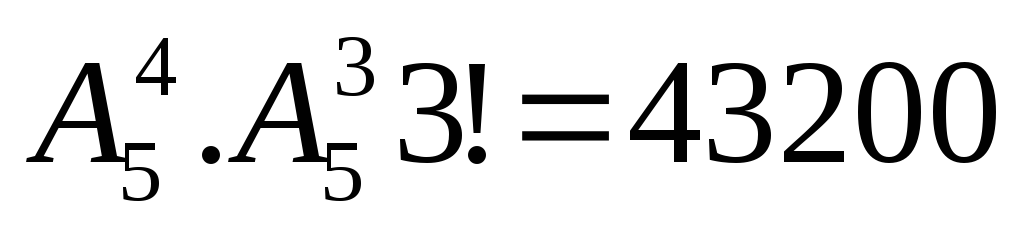

5. В почтовом отделении продаются открытки десяти видов в неограниченном количестве. Сколькими способами можно купить 12 открыток?

Имеем случай сочетания с повторениями:

.

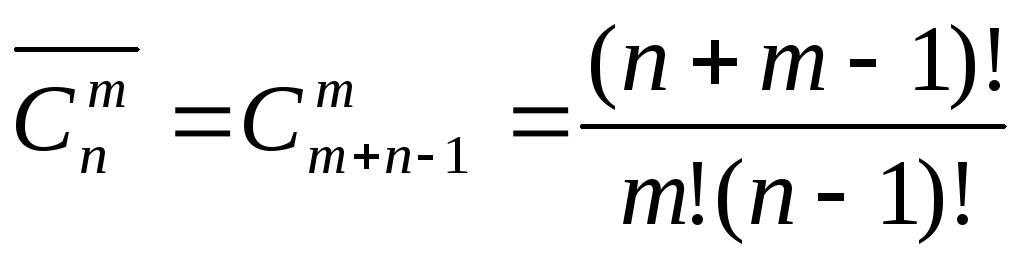
В нашей задаче 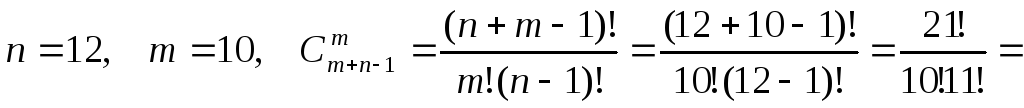352716.

6. В соревновании по гимнастике участвуют 10 человек практически одинаковых по степени мастерства. Трое судей должны независимо друг от друга пронумеровать их в порядке, отражающим их успехи в соревновании по мнению судей. Победителем считается тот, кого назовут первым хотя бы двое судей. В какой доле всех возможных случаев победитель будет определен?

Победитель будет определен в случаях, если А( ровно два судьи определили одного и того же спортсмена X), В( ровно три судьи назвали одного и того же спортсмена X).

, .

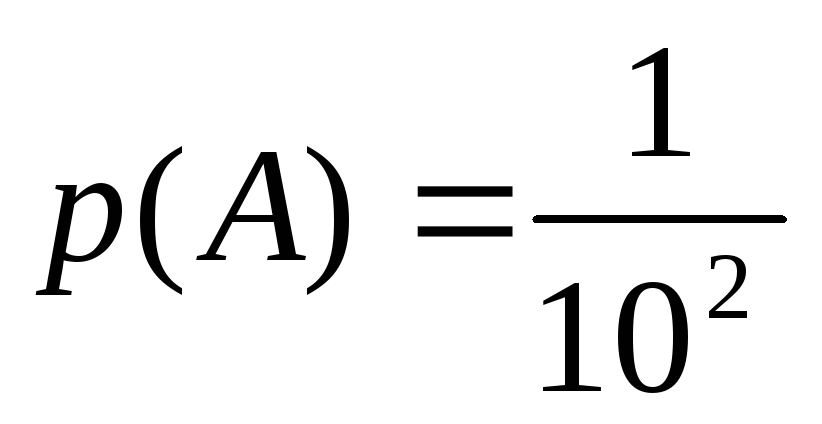
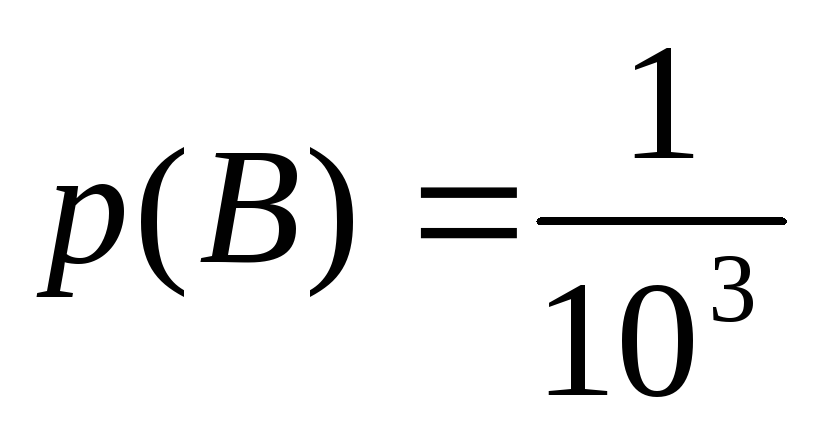
Однако спортсмен X – любой из 10 спортсменов, поэтому доля всех возможных случаев 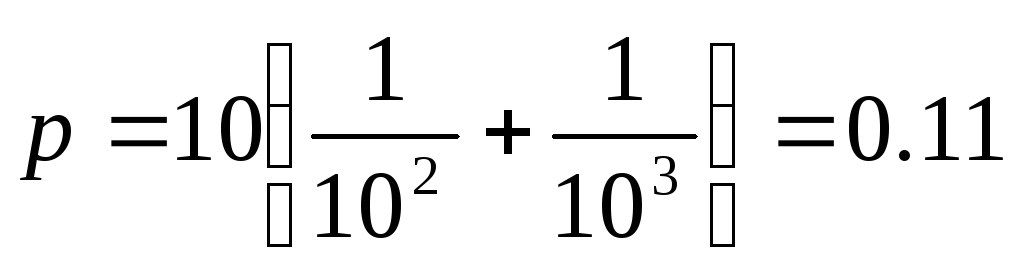, или 11%.

7. В урне лежат 10 жетонов с числами 1,2,3, . 10. Из нее, не выбирая, вынимают 3 жетона. Во скольких случаях сумма написанных на них чисел не меньше 9?

Неблагоприятные исходы: (1,2,3), (1,2,4), (1,2,5), (1,3,4) (в этих случаях сумма чисел меньше 9). Всего исходов . Значит, всего благоприятных исходов

8. Человек имеет 6 друзей и в течения 20 дней приглашает к себе 3 из них так, что компания им разу не повторяется. Сколькими способами может он это сделать?

Выбрать 3 друзей из 6 можно 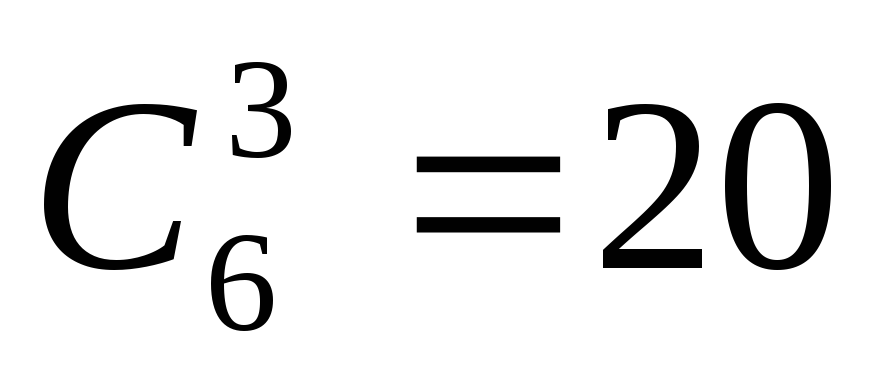способами. Значит, всего можно составить 20 различных компаний. Эти компании надо распределить на 20 дней. Это можно сделать 20!= 2432902008176640000 способами.

Ответ: 20! или 2 432 902 008 176 640 000 способов.

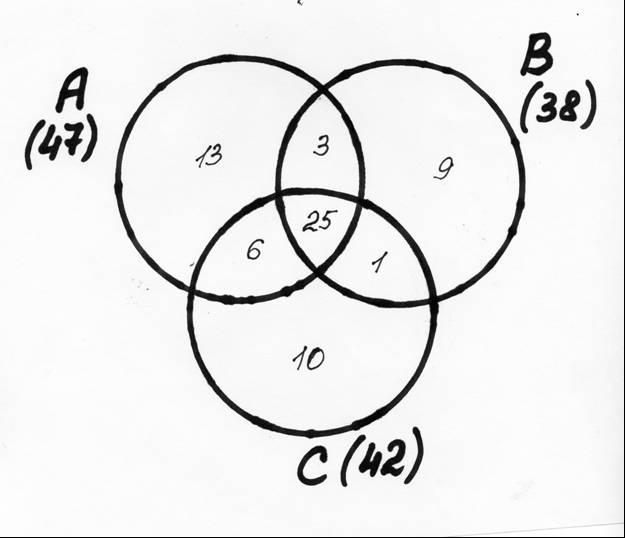
9. На загородную прогулку поехали 92 человека. Бутерброды с колбасой взяли 47 человек, с сыром – 38 человек, с ветчиной – 42 человека, и с сыром и с колбасой – 28 человек; и с колбасой и с ветчиной – 31 человек, и с сыром и с ветчиной – 26 человек. Все три вида бутербродов взяли 25 человек, а несколько человек вместо бутербродов захватили с собой пирожки. Сколько человек взяли с собой пирожки?

Решение задачи становится очевидно, если описать условие с помощью диаграммы Венна (в виде пересекающихся кругов, изображающих множества), приняв следующие обозначения:

А — множество туристов, которые взяли с собой бутерброды с колбасой;

В — множество туристов, которые взяли с собой бутерброды с сыром;

С — множество туристов, которые взяли с собой бутерброды с ветчиной.

Рис. 2. Диаграмма Венна.

На этой диаграмме видно:

а) Количество туристов, взявших с собой бутерброды всех трех видов (25).

б) Количество туристов, взявших с собой бутерброды каких-либо двух видов (с учетом туристов, взявших с собой бутерброды всех трех видов) – соответственно 3, 1 и 6 человек (чтобы общее число этих людей в соответствии с условием было равно 28, 26 и 31 человек).

в) Количество туристов, взявших с собой бутерброды какого-либо одного вида (с учетом туристов, перечисленных в пунктах а и б) – соответственно 13, 9 и 10 человек (чтобы общее число этих людей в соответствии с условием было равно 47, 38 и 42 человека).

Тогда общее число любителей бутербродов составит

25 + 3 + 1 + 6 + 13 + 9 + 10 = 67 человек.

Следовательно, пирожки взяли с собой 92 – 67 = 25 человек.

Источник

Имеется 6 пар перчаток различных размеров сколькими способами можно выбрать

Студент

Группа: Продвинутые
Сообщений: 58
Регистрация: 26.3.2007
Город: Москва
Учебное заведение: МГПУ, РГГУ
Вы: студент

Доброго времени суток.

Имеется 6 пар перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую руку и одну – на правую так, чтобы выбранные перчатки были разных размеров?

Подскажите, пожалуйста, с чего начать, или аналогичную задачу — мозг в 7 утра уже не соображает. (IMG:style_emoticons/default/blink.gif)

Доцент

Группа: Преподаватели
Сообщений: 3 615
Регистрация: 27.2.2007
Город: Екатеринбург
Вы: преподаватель

Доброго времени суток.

Имеется 6 пар перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую руку и одну – на правую так, чтобы выбранные перчатки были разных размеров?

Подскажите, пожалуйста, с чего начать, или аналогичную задачу — мозг в 7 утра уже не соображает. (IMG:style_emoticons/default/blink.gif)

Выбрать перчатку на левую руку можно 6 способами. При каждом таком выборе левой перчатки можно 5 способами выбрать правую перчатку, не совпадающую по размеру с выбранной левой.
По правилу произведения то, о чем спрашивается, можно выбрать 6*5=30 способами.

Студент

Группа: Продвинутые
Сообщений: 58
Регистрация: 26.3.2007
Город: Москва
Учебное заведение: МГПУ, РГГУ
Вы: студент

Источник

Имеется 6 пар перчаток различных размеров сколькими способами можно выбрать

Студент

Группа: Продвинутые
Сообщений: 58
Регистрация: 26.3.2007
Город: Москва
Учебное заведение: МГПУ, РГГУ
Вы: студент

Доброго времени суток.

Имеется 6 пар перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую руку и одну – на правую так, чтобы выбранные перчатки были разных размеров?

Подскажите, пожалуйста, с чего начать, или аналогичную задачу — мозг в 7 утра уже не соображает. (IMG:style_emoticons/default/blink.gif)

Доцент

Группа: Преподаватели
Сообщений: 3 615
Регистрация: 27.2.2007
Город: Екатеринбург
Вы: преподаватель

Доброго времени суток.

Имеется 6 пар перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую руку и одну – на правую так, чтобы выбранные перчатки были разных размеров?

Подскажите, пожалуйста, с чего начать, или аналогичную задачу — мозг в 7 утра уже не соображает. (IMG:style_emoticons/default/blink.gif)

Выбрать перчатку на левую руку можно 6 способами. При каждом таком выборе левой перчатки можно 5 способами выбрать правую перчатку, не совпадающую по размеру с выбранной левой.
По правилу произведения то, о чем спрашивается, можно выбрать 6*5=30 способами.

Студент

Группа: Продвинутые
Сообщений: 58
Регистрация: 26.3.2007
Город: Москва
Учебное заведение: МГПУ, РГГУ
Вы: студент

Источник