Имеется 20 наименований товаров сколькими способами их можно распределит
Вопрос по математике:
Имеется 20 наименований товаров. Сколькими способами их можно распределить по 3 магазинам, если известно, что в первый магазин должно быть доставлено 8 наименований, во второй 7 наименований, в третий 5 наименований.
Ответы и объяснения 1
Если ничего не путаю, то число будет огромным.
Это будет C=С(8/20)*С(7/12).
С(8/20)=20!/(8!*12!);
C(7/12)=12!/(7!*5!);
C=(20!/(8!*12!))*(12!/(7!*5!));
C=20!/(8!*7!*5!);
C=99768240;
Вроде так как-то.
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.
Источник
КОМБИНАТОРИКА
Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.
Правила сложения и умножения в комбинаторике
Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.
Пример 1.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?
Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.
По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.
Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n1 способами, второе действие n2 способами, третье – n3 способами и так до k-го действия, которое можно выполнить nk способами, то все k действий вместе могут быть выполнены:
Пример 2.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?
Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.
После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.
По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.
Сочетания без повторений. Сочетания с повторениями
Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?
Пример 3.
Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:

Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m (

Пример 4.
В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.

Размещения без повторений. Размещения с повторениями
Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?
Пример 5.
В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?
В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:
Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.
Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?
Пример 6.
У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?
Можно считать, что опыт состоит в 5-кратном выборе с возращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5:

Перестановки без повторений. Перестановки с повторениями
Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?
Пример 7.
Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?
Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.
Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k
Пример 8.
Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?
Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно
ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»
Источник
Имеется 20 наименований товаров сколькими способами их можно распределит
Вопрос по математике:
Имеется 20 наименований товаров. Сколькими способами их можно распределить по 3 магазинам, если известно, что в первый магазин должно быть доставлено 8 наименований, во второй 7 наименований, в третий 5 наименований.
Ответы и объяснения 1
Если ничего не путаю, то число будет огромным.
Это будет C=С(8/20)*С(7/12).
С(8/20)=20!/(8!*12!);
C(7/12)=12!/(7!*5!);
C=(20!/(8!*12!))*(12!/(7!*5!));
C=20!/(8!*7!*5!);
C=99768240;
Вроде так как-то.
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.
Источник
Задачи для самостоятельного решения
Дата добавления: 2015-07-23 ; просмотров: 4116 ; Нарушение авторских прав
Задача 1.Сколькими способами можно составить трехцветный полосатый флаг, если имеется материал пяти различных цветов? (Ответ: 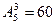
Задача 2.Сколькими способами можно поставить в ряд 5 человек для фотоснимка? (Ответ: 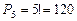
Задача 3.Сколькими способами могут 7 человек встать в очередь за билетами в театральной кассе? (Ответ: 7!)
Задача 4.Сколько существует различных пятизначных четных чисел, которые начинаются цифрой «2» и оканчиваются цифрой «4», если используются цифры 1,2, 3, 4, 5? (Ответ: 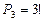
Задача 5.Сколькими способами можно выбрать три различные краски из имеющихся пяти? (Ответ: 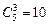
Задача 6.Сколькими способами можно составить набор из 8 пирожных, если имеется 4 сорта пирожных? (Ответ: 
Задача 7.Решить неравенство: 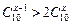
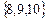
Задача 8.Экзамен по математике сдавали 250 абитуриентов, оценку ниже 5 получили 180 человек, а выдержали экзамен 210 абитуриентов. Сколько человек получили оценки 3 и 4? (Ответ: 140)
Задача 9. При обследовании читательских вкусов студентов оказалось, что 60% студентов читает журнал А, 50% журнал В, 50% – журнал С, 30% – журналы А и В, 20% – журналы В и С, 40% – журналы А и С, 10% – журналы А, В и С. Какой процент студентов: а) не читает ни одного из этих журналов? б) читает в точности два журнала? (Ответ: а) 20%, б) 60%)
Задача 10. Сколькими способами можно выбрать гласную и согласную буквы из букв слова «студент»? (Ответ: 10 способов)
Задача 11. Имеется пять видов конвертов без марок и 4 вида марок. Сколькими способами можно выбрать конверт и марку для посылки письма? (Ответ: 20)
Задача 12. В группе 35 студентов. Из них 20 посещают математический кружок, 11 – физический, 10 – не посещают ни одного из этих кружков. Сколько студентов посещают оба кружка? Сколько студентов посещают только математический кружок? (Ответ: 6;14)
Задача 13. На полке стоят 12 книг. Сколькими способами можно выбрать из них 5 книг так, чтобы никакие две из них не стояли рядом. (Ответ: 56)
Задача 14. При опросе 13 человек, каждый из которых знает по-крайней мере один иностранный язык, выяснилось, что 10 человек знают английский язык, 7 – немецкий, 6 – испанский, 5 – английский и немецкий, 4 – английский и испанский, 3 – немецкий и испанский. Сколько человек знают: a) все три языка?, б) ровно два языка?, в) только английский язык. (Ответ: 2, 6, 3)
Задача 15. Четверо студентов сдают экзамен. Сколькими способами могут быть поставлены им отметки, если известно, что никто из них не получил неудовлетворительной отметки? (Ответ: 81)
Задача 16. Два почтальона должны разнести 10 писем по 10 адресам. Сколькими способами они могут распределить работу? (Ответ: 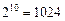
Задача 17. Сколькими способами могут быть присуждены 1-я, 2-я, 3-я премии трем лицам, если число соревнующихся равно 10? (Ответ: 720)
Задача 18. Сколькими способами можно рассадить 12 человек за круглым столом? (Ответ: 11!)
Задача 19. Имеется 20 наименований товаров. Сколькими способами их можно распределить по трем магазинам, если известно, что в первый магазин должно быть доставлено 8 наименований, во второй — 7 наименований и в третий – 5 наименований товаров? (Ответ: 
Задача 20. В почтовом отделении продаются открытки 10 сортов. Сколькими способами можно купить в нем 12 открыток? (Ответ: 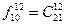
Задача 21. 6 одинаковых предметов распределяются по трем ящикам. Сколькими способами можно это сделать, если каждый ящик может вместить все 6 предметов? (Ответ: 28)
Задача 22. В школьной библиотеке имеются 6 экземпляров романа И.С. Тургенева «Рудин», 3 экземпляра романа «Дворянское гнездо» и 4 экземпляра романа «Отцы и дети». Кроме того, есть 5 томов, содержащих романы «Рудин» и «Дворянское гнездо», и 7 томов, содержащих романы «Дворянское гнездо» и «Отцы и дети». Сколькими способами можно взять в библиотеке все три романа так, чтобы ни один не был взят дважды? (Ответ: 134)
Задача 23. Сколько словарей надо издать, чтобы можно было непосредственно выполнять переводы с любого из пяти языков: русского, английского, немецкого, французского и испанского – на любой другой из этих языков? (Ответ: 20)
Задача 24. В фортепианном кружке занимаются 10 человек, в кружке художественного слова – 15, в вокальном кружке – 12 и в фотокружке – 20 человек. Сколькими способами можно составить группу из четырех чтецов, трех пианистов, пяти певцов и одного фотографа? (Ответ: 
Задача 25. Собрание из 80 человек выбирает председателя, секретаря и трех членов редакционной комиссии. Сколькими способами это можно сделать? (Ответ: 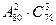
Задача 26. У одного студента есть 7 книг по математике, а у другого – 9 книг. Сколькими способами они могут обменять друг с другом по две книги? (Ответ: 756)
Задача 27. У мамы 10 яблок и 5 груш. Каждый день в течение 15 дней подряд она выдает по одному фрукту? Сколькими способами это может быть сделано? (Ответ: 3003)
Задача 28. Сколько решений имеет уравнение
при условии, что 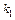
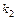
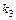
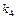
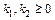

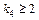
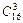
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Назначение теории множеств.
2. Дать определение множества, его обозначения. Привести примеры.
3. Какие множества называют равными?
4. Какие существуют основные принципы интуитивной объемности. На чем они основаны?
5. Как определяют мощность множества?
6. Перечислить основные парадоксы теории множеств. Пояснить их смысл.
7. Какие существуют основные операции над множествами?
8. Дать определение объединения двух множеств, привести пример.
9. Дать определение пересечения двух множеств, привести пример.
10. Дать определение разности двух множеств, привести пример.
11. Дать определение симметрической разности, привести пример.
12. Дать определение дополнения множества, привести пример.
13. Какое множество называют универсальным?
14. Когда используют диаграммы Эйлера-Венна?
15. Какие задачи решает комбинаторика?
16. Принцип умножения, расчетная формула.
17. Принцип сложения, расчетная формула.
18. Принцип разбиения множеств. Привести пример.
19. Принцип подсчета элементов дополнения. Привести пример.
20. Перечислить основные комбинаторные формулы.
21. Дать определение выборки. Какую выборку называют упорядоченной, неупорядоченной?
22. Какая выборка называется с повторениями, без повторений. Привести примеры указанных выборок.
23. Дать определение перестановки, привести формулу ее подсчета.
24. Дать определение размещения, привести формулу его подсчета.
25. Дать определение сочетания, привести формулу его подсчета.
26. Перечислить основные свойства биномиальных коэффициентов.
27. Дать определение перестановки с повторениями, привести формулу ее подсчета.
28. Дать определение размещения с повторениями, привести формулу его подсчета.
29. Дать определение сочетания с повторениями, привести формулу его подсчета.
30. Записать формулу включений и исключений, пояснить ее смысл.
Список литературы
1. Булгакова И.Н., Федотенко Г.Ф. Дискретная математика. Элементы теории. Задачи и упражнения: Учеб. Пособие. – Воронеж: Из-во ВГУ, 2004. – 62 с.
2. Гэри Хаггард, Джон Шлипф, Сью Уайтсайдс. Дискретная математика для программистов: учебное пособие / кол. авторов; пер. с анг. под. ред. А.А. Сапоженко. – М.: БИНОМ. Лаборатория знаний, 2010. – 627 с.
3. Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. – 5-е изд., исправл. – М.: ФИЗ-МАТЛИТ, 2004. – 256 с.
4. МатБюро: Дискретная математика [Электронный ресурс]. URL: http: //www.matburo.ru/ex_dm.php (дата обращения: 2.04.12).
5. Палий И.А. Дискретная математика. Курс лекций. – М.: Эксмо, 2008. – 352 с.
6. Практикум по дискретной математике. Сост. В.И. Ермаков, Т.А. Ерохина, В.О. Локуциевский, М.Н. Максименко, О. Л. Шеметкова. – М.: Изд-во Рос. экон. акад. имени Г.В. Плеханова, 2007. – 91 с.
7. Шапорев С.Д. Дискретная математика. Курс лекций и практических занятий. – СПб.: БХВ – Петербург, 2006. – 400 с.
Пинаев Виктор Алексеевич,
Славолюбова Ярославна Викторовна
Источник