Игральный кубик бросают 2 раза сколько способов набрать сумму очков 9

Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 4. Какова вероятность того, что потребовалось сделать три броска? Ответ округлите до сотых.

Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 3. Какова вероятность того, что был сделан один бросок? Ответ округлите до сотых.

Это задание ещё не решено, приводим решение прототипа.

Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 4. Какова вероятность того, что был сделан один бросок? Ответ округлите до сотых.

Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 3. Какова вероятность того, что было сделано два броска? Ответ округлите до сотых.

Это задание ещё не решено, приводим решение прототипа.

Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 3. Какова вероятность того, что было сделано три броска? Ответ округлите до сотых.

Это задание ещё не решено, приводим решение прототипа.

Аналоги к заданию № 508792: 508793 508794 508795 508796 Все

Источник

Игральный кубик бросают 2 раза сколько способов набрать сумму очков 9

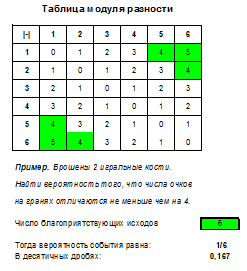
Игральную кость бросили два раза. Известно, что шесть очков не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 2».

Условию, что при двукратном броске игральной кости шесть очков не выпали ни разу, соответствует 25 исходов (отмечены оранжевым цветом). Событию «сумма выпавших очков равна 2» соответствует 1 из них (отмечены зелёным цветом). Значит, искомая вероятность равна

Игральную кость бросили два раза. Известно, что два очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 12».

Условию, что при двукратном броске игральной кости два очка не выпали ни разу, соответствует 25 исходов (отмечены оранжевым цветом). Событию «сумма выпавших очков равна 12» соответствует 1 из них (отмечены зелёным цветом). Значит, искомая вероятность равна

Игральную кость бросили два раза. Известно, что два очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 4».

Условию, что при двукратном броске игральной кости два очка не выпали ни разу, соответствует 25 исходов (отмечены оранжевым цветом). Событию «сумма выпавших очков равна 4» соответствуют 2 из них (отмечены зелёным цветом). Значит, искомая вероятность равна

Игральную кость бросили два раза. Известно, что четыре очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 11».

Условию, что при двукратном броске игральной кости четыре очка не выпали ни разу, соответствует 25 исходов (отмечены оранжевым цветом). Событию «сумма выпавших очков равна 11» соответствуют 2 из них (отмечены зелёным цветом). Значит, искомая вероятность равна

Источник

Игральный кубик бросают 2 раза сколько способов набрать сумму очков 9

Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, большее 3.

При бросании кубика равновозможны шесть различных исходов. Событию «выпадет больше трёх очков» удовлетворяют три случая: когда на кубике выпадает 4, 5, или 6 очков. Поэтому вероятность того, что на кубике выпадет не больше трёх очков равна Таким образом, при одном бросании кубика с одинаковой вероятностью реализуется либо событие А — выпало число, большее 3, либо событие Б — выпало число не больше 3. То есть равновероятно четыре события: А-А, А-Б, Б-А, Б-Б. Поэтому вероятность того, что оба раза выпало число, большее 3 равна

Игральную кость бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел равна 4 или 7.

Сумма двух выпавших чисел будет равна 4 в трех случаях(1 и 3, 3 и 1, 2 и 2) и 7 в шести случаях(1 и 6, 6 и 1, 2 и 5, 5 и 2, 3 и 4, 4 и 3), т. е. 9 благоприятных событий. А всего событий может быть 6 · 6 = 36, значит, вероятность равна

Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, меньшее 4.

При бросании кубика равновозможны шесть различных исходов. Событию «выпадет меньше четырёх очков» удовлетворяют три случая: когда на кубике выпадает 1, 2, или 3 очка. Поэтому вероятность того, что на кубике выпадет меньше четрёх очков равна Таким образом, при одном бросании кубика с одинаковой вероятностью реализуется либо событие А — выпало число, меньшее 4, либо событие Б — выпало число не меньше 4. То есть равновероятно четыре события: А-А, А-Б, Б-А, Б-Б. Поэтому вероятность того, что хотя бы раз выпало число, меньшее 4 равна

Игральную кость бросают дважды. Найдите вероятность того, что наибольшее из двух выпавших чисел равно 5.

При бросании кубика дважды равновозможны 6 · 6 = 36 различных исходов. Число 5 будет наибольшим из выпавших, если хотя бы один раз выпадает 5 и ни разу — 6. То есть либо на первом кубике должно выпасть 5 очков, а на втором — любое число кроме 6, либо наоборот, на втором кубике должно выпасть 5, а на первом — любое число кроме 6. Также необходимо помнить, что при таком подсчёте вариант, когда на обоих кубиках выпадает пять, мы учитываем дважды: 5 + 5 − 1 = 9. Поэтому вероятность того, что наибольшее из двух выпавших чисел — 5

Игральную кость бросают дважды. Найдите вероятность того, что наименьшее из двух выпавших чисел равно 2.

При бросании кубика дважды равновозможны 6 · 6 = 36 различных исходов. Число 2 будет наименьшим из выпавших, если хотя бы один раз выпадает 2 и ни разу — 1. То есть либо на первом кубике должно выпасть 2 очка, а на втором — любое число кроме 1, либо наоборот, на втором кубике должно выпасть 2, а на первом — любое число кроме 1. Также необходимо помнить, что при таком подсчёте вариант, когда на обоих кубиках выпадает двойка, мы учитываем дважды: 5 + 5 − 1 = 9. Поэтому вероятность того, что наименьшее из двух выпавших чисел — 2

Игральный кубик бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел четна.

При бросании кубика два раза равновозможны 6 · 6 = 36 различных исходов. Сумма чётна, если на первом кубике выпадает нечётное число и на втором выпадает нечётное число, этому соответствует 3 · 3 = 9 исходов. Либо, если на обоих кубиках выпадают чётные числа, этому соответствует 3 · 3 = 9 исходов. Поэтому вероятность того, что сумма двух выпавших чисел чётна равна

Игральную кость бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел нечетна.

При бросании кубика дважды равновозможны 6 · 6 = 36 различных исходов. Сумма нечётна, если на первом кубике выпадает нечётное число, а на втором выпадает чётное число, этому соответствует 3 · 3 = 9 исходов. Либо, если наоборот, на первом кубике выпадает чётное число, а на втором выпадает нечётное число, этому соответствует 3 · 3 = 9 исходов. Поэтому вероятность того, что сумма двух выпавших чисел нечётна равна

Игральную кость бросают дважды. Найдите вероятность того, что хотя бы раз выпало число, меньшее 4.

При бросании кубика равновозможны шесть различных исходов. Событию «выпадет меньше четырёх очков» удовлетворяет три случая: когда на кубике выпадает 1, 2, или 3 очка. Поэтому вероятность того, что на кубике выпадет меньше четырёх очков равна Таким образом, при одном бросании кубика с одинаковой вероятностью реализуется либо событие А — выпало число, меньшее 4, либо событие Б — выпало число не меньше 4. То есть равновероятно четыре события: А-А, А-Б, Б-А, Б-Б. Поэтому вероятность того, что хотя бы раз выпало число, меньшее 4 равна

Приведем другое решение.

Вероятность того, что на кубике выпадет меньше четырех очков, равно 0,5. Найдем вероятность противоположного события, состоящего в том, что на кубике выпадет не меньше четырех очков: 1&#8239− 0,5 = 0,5.

Вероятность того, что на обоих кубиках выпадут числа, не меньшие четырех, равна 0,5 · 0,5 = 0,25.

Событие «на обоих кубиках выпадут числа, не меньшие четырех очков» является противоположным событию «хотя бы один раз выпадет число, меньшее 4». Следовательно, вероятность того, что хотя бы один раз выпадет число, меньшее 4, равна 1 − 0,25 = 0,75

Источник

Решение задач о бросании игральных костей

Еще одна популярная задача теории вероятностей (наравне с задачей о подбрасывании монет) — задача о подбрасывании игральных костей.

Обычно задача звучит так: бросается одна или несколько игральных костей (обычно 2, реже 3). Необходимо найти вероятность того, что число очков равно 4, или сумма очков равна 10, или произведение числа очков делится на 2, или числа очков отличаются на 3 и так далее.

Основной метод решения подобных задач — использование формулы классической вероятности, который мы и разберем на примерах ниже.

Ознакомившись с методами решения, вы сможете скачать супер-полезный Excel-файл для расчета вероятности при бросании 2 игральных костей (с таблицами и примерами).

Одна игральная кость

С одной игральной костью дело обстоит до неприличия просто. Напомню, что вероятность находится по формуле $P=m/n$, где $n$ — число всех равновозможных элементарных исходов эксперимента с подбрасыванием кубика или кости, а $m$ — число тех исходов, которые благоприятствуют событию.

Пример 1. Игральная кость брошена один раз. Какова вероятность, что выпало четное число очков?

Так как игральная кость представляет собой кубик (еще говорят, правильная игральная кость, то есть кубик сбалансированный, так что выпадает на все грани с одинаковой вероятностью), граней у кубика 6 (с числом очков от 1 до 6, обычно обозначаемых точкам), то и общее число исходов в задаче $n=6$. Благоприятствуют событию только такие исходы, когда выпадет грань с 2, 4 или 6 очками (только четные), таких граней $m=3$. Тогда искомая вероятность равна $P=3/6=1/2=0.5$.

Пример 2. Брошен игральный кубик. Найти вероятность выпадения не менее 5 очков.

Рассуждаем также, как и в предыдущем примере. Общее число равновозможных исходов при бросании игрального кубика $n=6$, а условию «выпало не менее 5 очков», то есть «выпало или 5, или 6 очков» удовлетворяют 2 исхода, $m=2$. Нужная вероятность равна $P=2/6=1/3=0.333$.

Даже не вижу смысла приводить еще примеры, переходим к двум игральным костям, где все интереснее и сложнее.

Две игральные кости

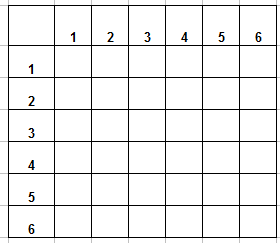
Когда речь идет о задачах с бросанием 2 костей, очень удобно использовать таблицу выпадения очков. По горизонтали отложим число очков, которое выпало на первой кости, по вертикали — число очков, выпавшее на второй кости. Получим такую заготовку (обычно я делаю ее в Excel, файл вы сможете скачать ниже):

А что же в ячейках таблицы, спросите вы? А это зависит от того, какую задачу мы будем решать. Будет задача про сумму очков — запишем туда сумму, про разность — запишем разность и так далее. Приступаем?

Пример 3. Одновременно бросают 2 игральные кости. Найти вероятность того, что в сумме выпадет менее 5 очков.

Сначала разберемся с общим числом исходов эксперимента. когда мы бросали одну кость, все было очевидно, 6 граней — 6 исходов. Здесь костей уже две, поэтому исходы можно представлять как упорядоченные пары чисел вида $(x,y)$, где $x$ — сколько очков выпало на первой кости (от 1 до 6), $y$ — сколько очков выпало на второй кости (от 1 до 6). Очевидно, что всего таких пар чисел будет $n=6\cdot 6=36$ (и им соответствуют как раз 36 ячеек в таблице исходов).

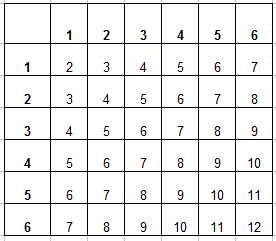
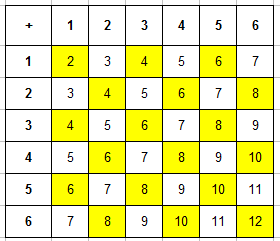
Вот и пришло время заполнять таблицу. В каждую ячейку занесем сумму числа очков выпавших на первой и второй кости и получим уже вот такую картину:

Теперь эта таблица поможем нам найти число благоприятствующих событию «в сумме выпадет менее 5 очков» исходов. Для этого подсчитаем число ячеек, в которых значение суммы будет меньше 5 (то есть 2, 3 или 4). Для наглядности закрасим эти ячейки, их будет $m=6$:

Тогда вероятность равна: $P=6/36=1/6$.

Пример 4. Брошены две игральные кости. Найти вероятность того, что произведение числа очков делится на 3.

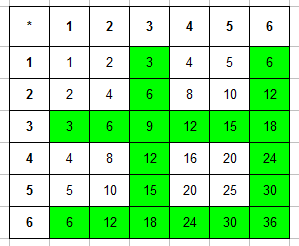
Составляем таблицу произведений очков, выпавших на первой и второй кости. Сразу выделяем в ней те числа, которые кратны 3:

Остается только записать, что общее число исходов $n=36$ (см. предыдущий пример, рассуждения такие же), а число благоприятствующих исходов (число закрашенных ячеек в таблице выше) $m=20$. Тогда вероятность события будет равной $P=20/36=5/9$.

Как видно, и этот тип задач при должной подготовке (разобрать еще пару тройку задач) решается быстро и просто. Сделаем для разнообразия еще одну задачу с другой таблицей (все таблицы можно будет скачать внизу страницы).

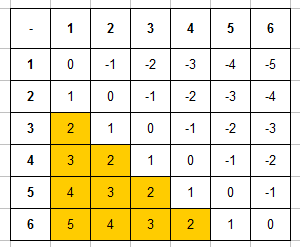
Пример 5. Игральную кость бросают дважды. Найти вероятность того, что разность числа очков на первой и второй кости будет от 2 до 5.

Запишем таблицу разностей очков, выделим в ней ячейки, в которых значение разности будет между 2 и 5:

Итак, что общее число равновозможных элементарных исходов $n=36$, а число благоприятствующих исходов (число закрашенных ячеек в таблице выше) $m=10$. Тогда вероятность события будет равной $P=10/36=5/18$.

Итак, в случае, когда речь идет о бросании 2 костей и простом событии, нужно построить таблицу, выделить в ней нужные ячейки и поделить их число на 36, это и будет вероятностью. Помимо задач на сумму, произведение и разность числа очков, также встречаются задачи на модуль разности, наименьшее и наибольшее выпавшее число очков (подходящие таблицы вы найдете в файле Excel).

Другие задачи про кости и кубики

Конечно, разобранными выше двумя классами задач про бросание костей дело не ограничивается (просто это наиболее часто встречаемые в задачниках и методичках), существуют и другие. Для разнообразия и понимания примерного способа решения разберем еще три типовых примера: на бросание 3 игральных костей, на условную вероятность и на формулу Бернулли.

Пример 6. Бросают 3 игральные кости. Найдите вероятность того, что в сумме выпало 15 очков.

В случае с 3 игральными костями таблицы составляют уже реже, так как их нужно будет аж 6 штук (а не одна, как выше), обходятся простым перебором нужных комбинаций.

Найдем общее число исходов эксперимента. Исходы можно представлять как упорядоченные тройки чисел вида $(x,y,z)$, где $x$ — сколько очков выпало на первой кости (от 1 до 6), $y$ — сколько очков выпало на второй кости (от 1 до 6), $z$ — сколько очков выпало на третьей кости (от 1 до 6). Очевидно, что всего таких троек чисел будет $n=6\cdot 6\cdot 6=216$ .

Теперь подберем такие исходы, которые дают в сумме 15 очков.

Получили $m=3+6+1=10$ исходов. Искомая вероятность $P=10/216=0.046$.

Пример 7. Бросают 2 игральные кости. Найти вероятность того, что на первой кости выпало не более 4 очков, при условии, что сумма очков четная.

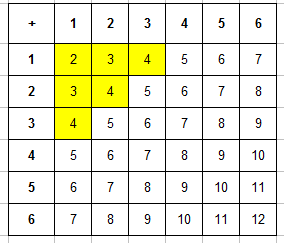
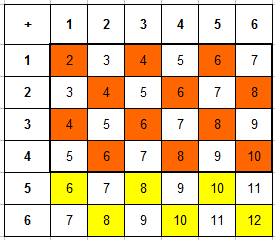
Наиболее простой способ решения этой задачи — снова воспользоваться таблицей (все будет наглядно), как и ранее. Выписываем таблицу сумм очков и выделяем только ячейки с четными значениями:

Получаем, что согласно условию эксперимента, всего есть не 36, а $n=18$ исходов (когда сумма очков четная).

Теперь из этих ячееек выберем только те, которые соответствуют событию «на первой кости выпало не более 4 очков» — то есть фактически ячейки в первых 4 строках таблицы (выделены оранжевым), их будет $m=12$.

Искомая вероятность $P=12/18=2/3.$

Эту же задачу можно решить по-другому, используя формулу условной вероятности. Введем события:
А = Сумма числа очков четная
В = На первой кости выпало не более 4 очков
АВ = Сумма числа очков четная и на первой кости выпало не более 4 очков
Тогда формула для искомой вероятности имеет вид: $$ P(B|A)=\frac. $$ Находим вероятности. Общее число исходов $n=36$, для события А число благоприятствующих исходов (см. таблицы выше) $m(A)=18$, а для события АВ — $m(AB)=12$. Получаем: $$ P(A)=\frac=\frac<18><36>=\frac<1><2>; \quad P(AB)=\frac=\frac<12><36>=\frac<1><3>;\\ P(B|A)=\frac=\frac<1><1>=\frac<2><3>. $$ Ответы совпали.

Пример 8. Игральный кубик брошен 4 раза. Найти вероятность того, что четное число очков выпадет ровно 3 раза.

В случае, когда игральный кубик бросается несколько раз, а речь в событии идет не о сумме, произведении и т.п. интегральных характеристиках, а лишь о количестве выпадений определенного типа, можно для вычисления вероятности использовать формулу Бернулли.

Итак, имеем $n=4$ независимых испытания (броски кубика), вероятность выпадения четного числа очков в одном испытании (при одном броске кубика) равна $p=3/6=1/2=0.5$ (см. выше задачи для одной игральной кости).

Тогда по формуле Бернулли $P=P_n(k)=C_n^k \cdot p^k \cdot (1-p)^$, подставляя $k=3$, найдем вероятность того, что четное число очков появится 3 раза: $$ P_4(3)=C_4^3 \cdot \left(1/2\right)^3 \cdot \left(1-1/2\right)^1=4 \cdot \left(1/2\right)^4=1/4=0,25. $$

Приведем еще пример, решаемый аналогичным образом.

Пример 9. Игральную кость бросают 8 раз. Найти вероятность того, что шестёрка появится хотя бы один раз.

Подставляем в формулу Бернулли следующие значения: $n=8$ (число бросков), $p=1/6$ (вероятность появления 6 при одном броске), $k\ge 1$ (хотя бы один раз появится шестерка). Прежде чем вычислять эту вероятность, напомню, что практически все задачи с формулировкой «хотя бы один. » удобно решать, переходя к противоположному событию «ни одного. «. В нашем примере сначала стоит найти вероятность события «Шестёрка не появится ни разу», то есть $k=0$: $$ P_8(0)=C_8^0 \cdot \left(1/6\right)^0 \cdot \left(1-1/6\right)^8=\left(5/6\right)^8. $$ Тогда искомая вероятность будет равна $$ P_8(k\ge 1)=1-P_8(0)=1-\left(5/6\right)^8=0.767. $$

Полезные ссылки

Для наглядного и удобного расчета вероятностей в случае бросания двух игральных костей я сделала
Файл с таблицами для расчета вероятности.

В нем приведены таблицы суммы, произведения, разности, минимума, максимума, модуля разности числа очков.

Вводя число благоприятствующих исходов в специальную ячейку вы получите рассчитанную вероятность (в обычных и десятичных дробях). Файл открывается программой Excel.

Еще по теории вероятностей:

В решебнике вы найдете более 400 задач о бросании игральных костей и кубиков с полными решениями (вводите часть текста для поиска своей задачи):

Источник