Хэш функция это способ

Хэш-алгоритмы

О себе

Студент кафедры информационной безопасности.

О хэшировании

В настоящее время практически ни одно приложение криптографии не обходится без использования хэширования.
Хэш-функции – это функции, предназначенные для «сжатия» произвольного сообщения или набора данных, записанных, как правило, в двоичном алфавите, в некоторую битовую комбинацию фиксированной длины, называемую сверткой. Хэш-функции имеют разнообразные применения при проведении статистических экспериментов, при тестировании логических устройств, при построении алгоритмов быстрого поиска и проверки целостности записей в базах данных. Основным требованием к хэш-функциям является равномерность распределения их значений при случайном выборе значений аргумента.
Криптографической хеш-функцией называется всякая хеш-функция, являющаяся криптостойкой, то есть удовлетворяющая ряду требований специфичных для криптографических приложений. В криптографии хэш-функции применяются для решения следующих задач:
— построения систем контроля целостности данных при их передаче или хранении,
— аутентификация источника данных.

Хэш-функцией называется всякая функция h:X -> Y, легко вычислимая и такая, что для любого сообщения M значение h(M) = H (свертка) имеет фиксированную битовую длину. X — множество всех сообщений, Y — множество двоичных векторов фиксированной длины.

Как правило хэш-функции строят на основе так называемых одношаговых сжимающих функций y = f(x₁, x₂) двух переменных, где x₁, x₂ и y — двоичные векторы длины m, n и n соответственно, причем n — длина свертки, а m — длина блока сообщения.
Для получения значения h(M) сообщение сначала разбивается на блоки длины m (при этом, если длина сообщения не кратна m то последний блок неким специальным образом дополняется до полного), а затем к полученным блокам M₁, M₂. M_N применяют следующую последовательную процедуру вычисления свертки:

Здесь v — некоторая константа, часто ее называют инициализирующим вектором. Она выбирается
из различных соображений и может представлять собой секретную константу или набор случайных данных (выборку даты и времени, например).
При таком подходе свойства хэш-функции полностью определяются свойствами одношаговой сжимающей функции.

Выделяют два важных вида криптографических хэш-функций — ключевые и бесключевые. Ключевые хэш-функции называют кодами аутентификации сообщений. Они дают возможность без дополнительных средств гарантировать как правильность источника данных, так и целостность данных в системах с доверяющими друг другу пользователями.
Бесключевые хэш-функции называются кодами обнаружения ошибок. Они дают возможность с помощью дополнительных средств (шифрования, например) гарантировать целостность данных. Эти хэш-функции могут применяться в системах как с доверяющими, так и не доверяющими друг другу пользователями.

О статистических свойствах и требованиях

Как я уже говорил основным требованием к хэш-функциям является равномерность распределения их значений при случайном выборе значений аргумента. Для криптографических хеш-функций также важно, чтобы при малейшем изменении аргумента значение функции сильно изменялось. Это называется лавинным эффектом.

К ключевым функциям хэширования предъявляются следующие требования:
— невозможность фабрикации,
— невозможность модификации.

Первое требование означает высокую сложность подбора сообщения с правильным значением свертки. Второе — высокую сложность подбора для заданного сообщения с известным значением свертки другого сообщения с правильным значением свертки.

К бесключевым функциям предъявляют требования:
— однонаправленность,
— устойчивость к коллизиям,
— устойчивость к нахождению второго прообраза.

Под однонаправленностью понимают высокую сложность нахождения сообщения по заданному значению свертки. Следует заметить что на данный момент нет используемых хэш-функций с доказанной однонаправленностью.
Под устойчивостью к коллизиям понимают сложность нахождения пары сообщений с одинаковыми значениями свертки. Обычно именно нахождение способа построения коллизий криптоаналитиками служит первым сигналом устаревания алгоритма и необходимости его скорой замены.
Под устойчивостью к нахождению второго прообраза понимают сложность нахождения второго сообщения с тем же значением свертки для заданного сообщения с известным значением свертки.

Это была теоретическая часть, которая пригодится нам в дальнейшем…

О популярных хэш-алгоритмах

Алгоритмы CRC16/32 — контрольная сумма (не криптографическое преобразование).

Алгоритмы MD2/4/5/6. Являются творением Рона Райвеста, одного из авторов алгоритма RSA.
Алгоритм MD5 имел некогда большую популярность, но первые предпосылки взлома появились еще в конце девяностых, и сейчас его популярность стремительно падает.
Алгоритм MD6 — очень интересный с конструктивной точки зрения алгоритм. Он выдвигался на конкурс SHA-3, но, к сожалению, авторы не успели довести его до кондиции, и в списке кандидатов, прошедших во второй раунд этот алгоритм отсутствует.

Алгоритмы линейки SHA Широко распространенные сейчас алгоритмы. Идет активный переход от SHA-1 к стандартам версии SHA-2. SHA-2 — собирательное название алгоритмов SHA224, SHA256, SHA384 и SHA512. SHA224 и SHA384 являются по сути аналогами SHA256 и SHA512 соответственно, только после расчета свертки часть информации в ней отбрасывается. Использовать их стоит лишь для обеспечения совместимости с оборудованием старых моделей.

Российский стандарт — ГОСТ 34.11-94.

Источник

Универсальное и идеальное хеширование

Начинаем неделю с полезного материала приуроченного к запуску курса «Алгоритмы для разработчиков». Приятного прочтения.

Хеширование — отличный практический инструмент, с интересной и тонкой теорией. Помимо использования в качестве словарной структуры данных, хеширование также встречается во многих различных областях, включая криптографию и теорию сложности. В этой лекции мы опишем два важных понятия: универсальное хеширование (также известное как универсальные семейства хеш-функций) и идеальное хеширование.

Материал, освещенный в этой лекции, включает в себя:

• Формальная постановка и общая идея хеширования.
• Универсальное хеширование.
• Идеальное хеширование.

2. Вступление

Мы рассмотрим основную проблему со словарем, которую мы обсуждали до этого, и рассмотрим две версии: статическую и динамическую:

• Статическая: дано множество элементов S, мы хотим хранить его таким образом, чтобы можно было быстро выполнять поиск.
• Например, фиксированный словарь.
• Динамическая: здесь у нас есть последовательность запросов на вставку, поиск и, возможно, удаление. Мы хотим сделать все это эффективно.

Для первой проблемы мы могли бы использовать отсортированный массив и двоичный поиск. Для второй мы могли бы использовать сбалансированное дерево поиска. Однако хеширование дает альтернативный подход, который зачастую является самым быстрым и удобным способом решения этих проблем. Например, предположим, что вы пишете программу для AI-поиска и хотите хранить ситуации, которые вы уже разрешили (позиции на доске или элементы пространства состояний), чтобы не повторять те же вычисления, при столкновении с ними снова. Хеширование обеспечивает простой способ хранения такой информации. Также существует множество применений в криптографии, сетях, теории сложности.

3. Основы хеширования

Формальная постановка для хеширования заключается в следующем.

• Ключи принадлежат некоторому большому множеству U. (Например, представьте, что U — набор всех строк длиной не более 80 символов ascii.)
• Есть некоторое множество ключей S в U, которое нам на самом деле нужно (ключи могут быть как статическими, так и динамическими). Пусть N = |S|. Представьте, что N гораздо меньше, чем размер U. Например, S — это множество имен учеников в классе, которое намного меньше, чем 128^80.
• Мы будем выполнять вставки и поиск с помощью массива A некоторого размера M и хеш-функции h: U → <0,…, М — 1>. Дан элемент x, идея хеширования состоит в том, что мы хотим хранить его в A[h(x)]. Обратите внимание, что если бы U было маленьким (например, 2-символьные строки), то можно было бы просто сохранить x в A[x], как в блочной сортировке. Проблема в том, что U большое, поэтому нам нужна хеш-функция.
• Нам нужен метод для разрешения коллизий. Коллизия — это когда h(x) = h(y) для двух разных ключей x и y. В этой лекции мы будем обрабатывать коллизии, определяя каждый элемент A как связанный список. Есть ряд других методов, но для проблем, на которых мы сосредоточимся здесь, это самый подходящий. Этот метод называется методом цепочек. Чтобы вставить элемент, мы просто помещаем его в начало списка. Если h — хорошая хеш-функция, то мы надеемся, что списки будут небольшими.

Одним из замечательных свойств хеширования является то, что все словарные операции невероятно просты в реализации. Чтобы выполнить поиск ключа x, просто вычислите индекс i = h(x) и затем идите по списку в A[i], пока не найдете его (или не выйдете из списка). Чтобы вставить, просто поместите новый элемент в верхней части его списка. Чтобы удалить, нужно просто выполнить операцию удаления в связанном списке. Теперь мы переходим к вопросу: что нам нужно для достижения хорошей производительности?

Желательные свойства. Основные желательные свойства для хорошей схемы хеширования:

1. Ключи хорошо рассредоточены, чтобы у нас не было слишком много коллизий, так как коллизии влияют на время выполнения поиска и удаления.
2. M = O(N): в частности, мы бы хотели, чтобы наша схема достигла свойства (1) без необходимости, чтобы размер таблицы M был намного больше, чем число элементов N.
3. Функция h должна быстро вычисляться. В нашем сегодняшнем анализе мы будем рассматривать время для вычисления h(x) как константу. Тем не менее, стоит помнить, что она не должна быть слишком сложной, потому что это влияет на общее время выполнения.

Учитывая это, время поиска элемента x равно O(размер списка A[h(x)]). То же самое верно для удалений. Вставки занимают время O(1) независимо от длины списков. Итак, мы хотим проанализировать, насколько большими получаются эти списки.

Базовая интуиция: один из способов красиво распределить элементы — это распределить их случайным образом. К сожалению, мы не можем просто использовать генератор случайных чисел, чтобы решить, куда направить следующий элемент, потому что тогда мы никогда не сможем найти его снова. Итак, мы хотим, чтобы h было чем-то «псевдослучайным» в некотором формальном смысле.

Сейчас мы изложим некоторые плохие новости, а затем некоторые хорошие.

Утверждение 1 (Плохие новости) Для любой хэш-функции h, если |U| ≥ (N −1) M +1, существует множество S из N элементов, которые все хешируются в одном месте.

Доказательство: по принципу Дирихле. В частности, чтобы рассмотреть контрапозиции, если бы каждое местоположение имело не более N — 1 элементов U, хэширующих его, то U мог бы иметь размер не более M (N — 1).

Отчасти поэтому хэширование кажется таким загадочным — как можно утверждать, что хэширование хорошо, если для любой хэш-функции вы можете придумать способы ее предотвращения? Один из ответов заключается в том, что существует множество простых хеш-функций, которые хорошо работают на практике для типичных множеств S. Но что, если мы хотим получить хорошую гарантию наихудшего случая?

Вот ключевая идея: давайте использовать рандомизацию в нашей конструкции h, по аналогии с рандомизированной быстрой сортировкой. (Само собой разумеется, h будет детерминированной функцией). Мы покажем, что для любой последовательности операций вставки и поиска (нам не нужно предполагать, что набор вставленных элементов S является случайным), если мы выберем h таким вероятностным способом, производительность h в этой последовательности будет хорошо в ожидании. Таким образом, это та же самая гарантия, что и в рандомизированной быстрой сортировке или ловушках. В частности, это идея универсального хеширования.

Как только мы разработаем эту идею, мы будем использовать ее для особенно приятного приложения под названием «идеальное хеширование».

4. Универсальное хеширование

Определение 1. Рандомизированный алгоритм H для построения хеш-функций h: U → <1, …, М>
универсален, если для всех x != y в U имеем

Мы также можем сказать, что множество H хеш-функций является универсальным семейством хеш-функций, если процедура «выбрать h ∈ H наугад» универсальна. (Здесь мы отождествляем множество функций с равномерным распределением по множеству.)

Теорема 2. Если H универсален, то для любого множества S ⊆ U размера N, для любого x ∈ U (например, который мы могли бы искать), если мы строим h случайным образом в соответствии с H, ожидаемое число коллизий между х и другими элементами в S не более N/M.

Доказательство: у каждого y ∈ S (y != x) есть не более 1 / M шанса столкновения с x по определению «универсального». Так,

• Пусть Cxy = 1, если x и y сталкиваются, и 0 в противном случае.
• Пусть Cx обозначает общее количество столкновений для x. Итак, Cx = Py∈S, y != x Cxy.
• Мы знаем, что E [Cxy] = Pr (x и y сталкиваются) ≤ 1 / M.
• Таким образом, по линейности ожидания E [Cx] = Py E [Cxy]

Источник

Что такое хэш и хэш-функция: практическое применение, обзор популярных алгоритмов

Цифровые технологии широко применяют хеширование, несмотря на то, что изобретению более 50 лет: аутентификация, осуществление проверки целостности информации, защита файлов, включая, в некоторых случаях, определение вредоносного программного обеспечения и многие другие функции. Например, множество задач в области информационных технологий требовательны к объему поступающих данных. Согласитесь, проще и быстрее сравнить 2 файла весом 1 Кб, чем такое же количество документов, но, к примеру, по 10 Гб каждый. Именно по этой причине алгоритмы, способные оперировать лаконичными значениями, весьма востребованы в современном мире цифровых технологий. Хеширование – как раз решает эту проблему. Разберемся подробно, что такое хэш и хэш-функция.

Интересно! Английский термин «Hash» (хэш) в переводе имеет множество значений – марихуана, мелкорубленое мясо, овощи, а также путаница, мешанина, или, если переводить на литературный русский, винегрет. В свою очередь процесс «Hashing» (хэширование или хеширование) так же имеет несколько переводов: рубка, перемешивание, крошение.

Что за «зверь» такой это хеширование?

Чтобы в головах читателей не образовался «винегрет», начнем со значения терминологий применительно к цифровым технологиям:

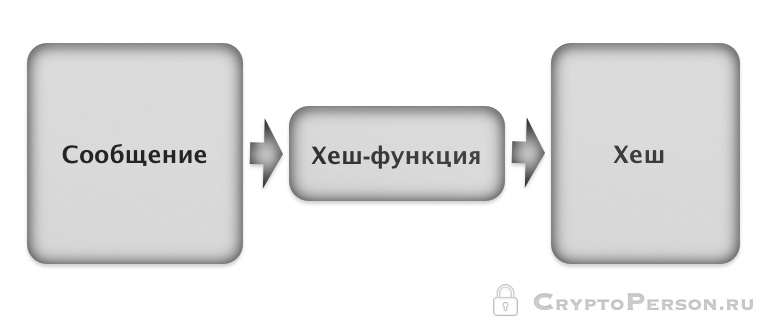
• хэш-функция («свертка») – математическое уравнение или алгоритм, предназначенный и позволяющий превратить входящий информационный поток неограниченного объема в лаконичную строчку с заданным количеством парных символов (число зависит от протокола);
• хеширование – процесс, описанный в предыдущем пункте;
• хэш (хэш-код, хэш-сумма) – та самая лаконичная строчка (блок) из нескольких десятков «случайно» подобранных символов или, другими словами, результат хеширования;
• коллизия – один и тот же хэш для разных наборов данных.

Исходя из пояснений, делаем вывод: хеширование – процесс сжатия входящего потока информации любого объема (хоть все труды Уильяма Шекспира) до короткой «аннотации» в виде набора случайных символов и цифр фиксированной длины.

Коллизии

Коллизии хэш-функций подразумевает появление общего хэш-кода на два различных массива информации. Неприятная ситуация возникает по причине сравнительно небольшого количества символов в хэш. Другими совами, чем меньше знаков использует конечная формула, тем больше вероятность итерации (повтора) одного и того же хэш-кода на разные наборы данных. Чтобы снизить риск появления коллизии, применяют двойное хеширование строк, образующее открытый и закрытый ключ – то есть, используется 2 протокола, как, например, в Bitcoin. Специалисты, вообще, рекомендуют обойтись без хеширования при осуществлении каких-либо ответственных проектов, если, конечно же, это возможно. Если без криптографической хэш-функции не обойтись, протокол обязательно нужно протестировать на совместимость с ключами.

Важно! Коллизии будут существовать всегда. Алгоритм хеширования, перерабатывающий различный по объему поток информации в фиксированный по количеству символов хэш-код, в любом случае будет выдавать дубли, так как множеству наборов данных противостоит одна и та же строчка заданной длины. Риск повторений можно только снизить.

Технические параметры

Основополагающие характеристики протоколов хеширования выглядят следующим образом:

1. Наличие внутрисистемных уравнений, позволяющих модифицировать нефиксированный объем информации в лаконичный набор знаков и цифр заданной длины.
2. Прозрачность для криптографического аудита.
3. Наличие функций, дающих возможность надежно кодировать первоначальную информацию.
4. Способность к расшифровке хэш-суммы с использованием вычислительного оборудования средней мощности.

Здесь стоит так же отметить важные свойства алгоритмов: способность «свертывать» любой массив данных, производить хэш конкретной длины, распределять равномерно на выходе значения функции. Необходимо заметить, любые изменения во входящем сообщении (другая буква, цифра, знак препинания, даже лишний пробел) внесут коррективы в итоговый хэш-код. Он просто будет другим – такой же длины, но с иными символами.

Требования

К эффективной во всех отношениях хэш-функции выдвигаются следующие требования:

• протокол должен обладать чувствительностью к изменениям, происходящим во входящих документах – то есть, алгоритм обязан распознавать перегруппировку абзацев, переносы, другие элементы текстовых данных (смысл текста не меняется, просто происходит его коррекция);
• технология обязана так преобразовывать поток информации, чтобы невозможно на практике осуществить обратную процедуру – восстановить из значения хэш первоначальные данные;
• протокол должен использовать такие математические уравнения, которые исключили или значительно снизили факт появления коллизии.

Данные требования выполнимы исключительно тогда, когда протокол базируется на сложных математических уравнениях.

Практическое применение

Процедура хеширования относительно своего функционала может быть нескольких типов:

1. Протокол для аудита целостности информации. В процессе передачи документов осуществляется вычисления хэш-кода. Результат передается вместе с документами. Прием информации сопровождается повторным вычислением хэш-кода с последующим сравнением, полученным значением. Несовпадение – ошибка. Этот алгоритм обладает высокими скоростными показателями при вычислении, но отличается нестабильностью и малым значением хэш-функции. Пример – протокол CRC-32, который имеет только 232 значения хэш, различающихся между собой.
2. Криптографический алгоритм. Внедряется в качестве защиты от несанкционированного доступа (взлома). Проверяет систему на предмет искажения информации в момент передачи файлов по сети. При таких обстоятельствах «правильный» хэш имеет свободный доступ, а ключ, полученного документа, вычисляется при помощи разнообразных софтов (программ). Пример – SHA-1, SHA-2, MD5, отличающихся стабильностью и сложнейшим уравнением поиска коллизий.
3. Протокол для создания эффективной информационной конструкции. Определяющая задача – структурирование информации в хэш-таблицы. Такая табличная структура делает возможным добавлять/удалять, находить нужные данные с невероятной скоростью.

Разберемся детальней в сфере применения протоколов хеширования.

Скачивание файлов из Всемирной Паутины

Этим занимается фактически каждый активный пользователь Всемогущей Сети, сталкиваясь с хэш-функциями сам того не осознавая, так как мало кто обращает внимание при скачивании того или иного файла на череду непонятных цифр и латинских букв. Однако именно они и есть хэш или контрольные суммы – перед вереницей символов стоит название используемой категории протокола хеширования. В общем-то, для обывателей абсолютно ненужная «инфа», а продвинутый юзер может выяснить, скачал ли он точную копию файла или произошла ошибка. Для этой процедуры необходимо установить на собственный ПК специальную утилиту (программу), которая способна вычислить хэш по представленному протоколу.

Важно! Установив на ПК пакет утилит, прогоняем через него файлы. Затем сравниваем полученный результат. Совпадение символов говорит о правильной копии – соответствующей оригиналу. Обнаруженные различия подразумевают повторное скачивание файла.

Алгоритм и электронно-цифровая подпись (ЭЦП)

Цифровая резолюция (подпись) – кодирование документа с использованием ключей закрытого и открытого типа. Другими словами, первоначальный документ сопровождается сообщением, закодированным закрытым ключом. Проверка подлинности электронной подписи осуществляется с применением открытого ключа. При обстоятельствах, когда в ходе сравнения хэш двух информационных наборов идентичен, документ, который получил адресат, признается оригинальным, а подпись истинной. В сухом остатке получаем высокую скорость обработки потока наборов данных, эффективную защиту виртуального факсимиле, так как подпись обеспечивается криптографической стойкостью. В качестве бонуса – хэш подразумевает использование ЭЦП под разнообразными типами информации, а не только текстовыми файлами.

Ревизия паролей

Очередная область применения хэш-функции, с которой сталкивается практически каждый пользователь. Подавляющее большинство серверов хранит пользовательские пароли в значении хэш. Что вполне обоснованно, так как, сберегая пароли пользователей в обычной текстовой форме, можно забыть о безопасности конфиденциальных, секретных данных. Столкнувшись с хэш-кодом, хакер даже время терять не будет, потому что, обратить вспять произвольный набор символов практически невозможно. Конечно же, если это не пароль в виде «12345» или что-то на подобии него. Доступ осуществляется путем сравнения хэш-кода вводимого юзером с тем, который хранится на сервере ресурса. Ревизию кодов может осуществлять простейшая хэш-функция.

Важно! В реальности программисты применяют многоярусный комплексный криптографический протокол с добавлением, в большинстве случаев, дополнительной меры безопасности – защищенного канала связи, чтобы виртуальные мошенники не перехватили пользовательский код до того, как он пройдет проверку на сервере.

Как появилось понятие хэш?

Сделаем небольшую паузу, чтобы интеллект окончательно не поплыл от потока сложных для простых пользователей терминов и информации. Расскажем об истории появления термина «хэш». А для простоты понимания выложим «инфу» в табличной форме.

Дата (год)	Хронология событий
1953	Известный математик и программист Дональд Кнут авторитетно считает, что именно в этот промежуток времени сотрудник IBM Ханс Питер Лун впервые предложил идею хеширования.
1956	Арнольд Думи явил миру такой принцип хеширования, какой знают его подавляющее большинство современных программистов. Именно эта «светлая голова» предложила считать хэш-кодом остаток деления на любое простое число. Кроме этого, исследователь видел идеальное хеширование инструментов для позитивной реализации «Проблемы словаря».
1957	Статья Уэсли Питерсона, опубликованная в «Journal of Research and Development», впервые серьезно затронула поиск информации в больших файлах, определив открытую адресацию и ухудшение производительности при ликвидации.
1963	Опубликован труд Вернера Бухгольца, где было представлено доскональное исследование хэш-функции.
1967	В труде «Принципы цифровых вычислительных систем» авторства Херберта Хеллермана впервые упомянута современная модель хеширования.
1968	Внушительный обзор Роберта Морриса, опубликованный в «Communications of the ACM», считается точкой отсчета появления в научном мире понятия хеширования и термина «хэш».

Интересно! Еще в 1956 году советский программист Андрей Ершов называл процесс хеширования расстановкой, а коллизии хэш-функций – конфликтом. К сожалению, ни один из этих терминов не прижился.

Стандарты хеширования: популярные варианты

Итак, от экскурса в историю перейдем вновь к серьезной теме. Опять-таки, ради простоты восприятия предлагаем краткое описание популярных стандартов хеширования в табличном виде. Так проще оценить информацию и провести сравнение.

Название	Краткий обзор
CRC-32	Полином CRC (Cyclic Redundancy Check, что значит «циклическая проверка излишков»). Является мощным легко осуществимым методом хеширования для достижения надежности информации. Применяется для защиты данных и обнаружении ошибок в потоке информации. Популярность принесли следующие качества: высочайшая степень обнаружения ошибок, минимальные расходы, простота эксплуатирования. Генерирует 32-битный хэш. Используется комитетом по стандартам локальных систем.
MD5	Протокол базируется на 128-битном (16-байтном) фундаменте. Применяется для хранения паролей, создания уникальных криптографических ключей и ЭЦП. Используется для аудита подлинности и целостности документов в ПК. Недостаток – сравнительно легкое нахождение коллизий.
SHA-1	Реализует хеширование и шифрование по принципу сжатия. Входы такого алгоритма сжатия состоят из набора данных длиной 512 Бит и выходом предыдущего блока. Количество раундов – 80. Размер значения хэш – 32 Бит. Найденные коллизии – 2 52 операции. Рекомендовано для основного использования в госструктурах США.
SHA-2	Семейство протоколов – однонаправленных криптографических алгоритмов, куда входит легендарный SHA-256, используемый в Bitcoin. Размер блока – 512/1024 Бит. Количество раундов 64/80. Найденных коллизий не существует. Размер значения однонаправленных хэш-функций – 32 Бит.
ГОСТ Р 34.11-2012 «Стрибог»	Детище отечественных программистов, состоящее из пары хэш-функций, с длинами итогового значения 256 и 512 Бит, отличающиеся начальным состоянием и результатом вычисления. Криптографическая стойкость – 2 128 . Преобразование массива данных основано на S-блоках, что существенно осложняет поиск коллизий.

На этом, пожалуй, закончим экскурсию в мир сложных, но весьма полезных и востребованных протоколов хеширования.

Источник