Характеристический способ задания множества примеры

ФизМат

вторник, 11 декабря 2012 г.

[Билет 1] Множества. Способы задания множеств. Характеристическое свойство множеств. Равные множества, подмножества. Универсальное множество. Конечные и бесконечные множества. Пустое множество. Основные числовые и геометрические множества.

Множества.


Множество — совокупность различных элементов, мыслимая как единое целое

Элемент множества — объект А называется элементом множества, если он обладает характеристическим свойствами этого множества.

Способы задания множеств.

1) Перечислением — и перечислении множества его элементы принято заключать в фигурные скобки:
< 2 , 4 , 6 , . . . >— множество четных чисел,
< 3 , 6 , 9 , . . . >— множество чисел кратных трем.
Под многоточием в данных случаях подразумеваются все последующие числа: в первом случае — четные, а во втором — кратные трем.

2) Описание свойств — для задания (описания) некоторого множества
, состоящего из элементов, обладающих свойством , используют запись . Читается как: « — множество элементов таких, что «. Например, — множество натуральных чисел, меньших 7.

Характеристическое свойство множеств.

Характеристическое свойство – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, не принадлежащий ему.

Равные множества, подмножества.

Универсальное множество.

Определение: Универсальное множество — это такое множество, которое состоит из всех элементов, а так же подмножеств множества объектов исследуемой области

Конечные и бесконечные множества.

Множества, состоящие из бесконечного числа элементов называются бесконечными, из конечного — конечными

Пустое множество.

Множество, не содержащее ни одного элемента, называется пустым. ∅

Основные числовые и геометрические множества.

Z− множество целых чисел;
Q− множество рациональных чисел;
I− множество иррациональных чисел;
R− множество действительных чисел;
C− множество комплексных чисел.

Источник

Метод характеристических функций в теории множеств

Доказательство сложных теоретико-множественных тождеств методом двух включений часто бывает довольно громоздким, и при построении доказательства ход рассуждений не всегда очевиден. Одним из методов, не требующих «угадывания» пути доказательства, является метод характеристических функций.

Характеристическая функция множества есть функция, отображающая универсальное множество в двухэлементное множество

Из определения характеристической функции множества вытекает справедливость тождества

Выразим характеристическую функцию пересечения множеств и через характеристические функции и этих множеств. Из определения пересечения следует, что искомая характеристическая функция должна принимать значение 1 для тех элементов , которые принадлежат множествам и одновременно, и значение 0 в противном случае. Легко видеть, что функция

удовлетворяет этому требованию.

Можно предположить, что характеристическая функция объединения множеств и будет равна сумме характеристических функций множеств. Однако так ее определить нельзя, поскольку для элементов такая сумма будет иметь значение 2. Введем «поправку» и в результате получим искомую формулу:

Непосредственно из определения — дополнения множества — следует, что

Для разности характеристическая функция имеет вид

а для симметрической разности —

Отметим, что последнюю формулу можно получить, опираясь на свойство 19 и тождество (1.10), а также на характеристические функции для пересечения, объединения и разности:

С учетом равенства (1.10) полученную формулу можно записать в виде

Метод характеристических функций доказательства справедливости теоретико-множественного тождества заключается в выражении характеристических функций обеих его частей через характеристические функции входящих в него множеств. Тождество верно тогда и только тогда, когда характеристические функции левой и правой частей совпадают.

Пример 1.22. Используя метод характеристических функций, выясним, справедливо ли тождество

С одной стороны,

С другой стороны,

Характеристические функции левой и правой частей тождества совпадают. Следовательно, тождество верно.

Пример 1.23. Выясним, является ли тождеством следующее выражение:

С одной стороны,

С другой стороны,

Легко видеть, что получены разные характеристические функции. Например,при и имеем

Таким образом, доказано, что .

Отметим, что метод характеристических функций не является универсальным. Так, его нельзя использовать при доказательстве тождеств, содержащих декартово произведение множеств, в частности, тождеств для соответствий (бинарных отношений).

Источник

Способы задания множеств.

ПЛАН

1. Понятие множества.

2. Способы задания множеств.

3. Отношения между множествами.

4. Операции над множествами.

5. Свойства операций над множествами.

6. Понятие «система счисления».

7. Непозиционная система счисления.

8. Позиционная система счисления.

9. Перевод чисел из одной системы счисления в другую.

Понятие множества.

Для сокращенной записи будем использовать следующие символы:

• a Î A — а является элементом множества А;

• a Ï A — а не является элементом множества А;

• — пустое множество;

• <a, d, с> — множество, состоящее из трех элементов a, d и с;

• <х|Р(х)> — множество, состоящее из таких элементов х, для которых истинно утверждение Р(х);

• A È B — объединение множеств A и В;

• A Ç B — пересечение множеств А и В;

• A Ì B — А является подмножеством В;

• — дополнение множества А до универсального множества;

• U — универсальное множество;

• a R b — между a и b существует бинарное отношение R.

Множество является самым широким понятием в математике и поэтому принимается без определения. Множество считается заданным, если относительно каждого объекта можно сказать, принадлежит он данному множеству или нет. Поэтому обычно говорят о множестве как о наборе предметов (элементов множества), наделённых определёнными общими свойствами. Множество книг в библиотеке, множество автомобилей на стоянке, множество звёзд на небосводе, растительный и животный мир Земли — всё это примеры множеств.

Конечное множество состоит из конечного числа элементов, например, множество страниц в книге, множество учеников в школе и т.д.

Пустое множество ( ) не содержит ни одного элемента, например, множество крылатых слонов, множество корней уравнения sin x = 2 и т.д.

Бесконечное множество состоит из бесконечного числа элементов, т.е. это множество, которое не является ни конечным, ни пустым. Примеры: множество действительных чисел, множество точек плоскости, множество атомов во Вселенной и т.д.

Счётное множество — множество, элементы которого можно пронумеровать. Например, множества натуральных, чётных, нечётных чисел. Счётное множество может быть конечным (множество книг в библиотеке) или бесконечным (множество целых чисел, его элементы можно пронумеровать следующим образом:

элементы множества: . -5, — 4, -3, -2, -1, 0, 1, 2, 3, 4, 5, .

номера элементов: . 11 9 7 5 3 1 2 4 6 8 10 . ).

Несчётное множество — множество, элементы которого невозможно пронумеровать. Например, множество действительных чисел. Несчётное множество может быть только бесконечным.

Выпуклое множество — множество, которое наряду с любыми двумя точками А и В содержит также весь отрезок АВ. Примеры выпуклых множеств: прямая, плоскость, круг. Однако, окружность не является выпуклым множеством.

Способы задания множеств.

Если объект a является элементом множества A, то говорят, что a принадлежит A, и записывают a A . Запись a Ï A означает, что a не принадлежит A.

Множество может быть задано следующим образом:

• перечислением всех его элементов по их названиям (так описываются множество книг в библиотеке, множество учеников в классе, алфавит любого языка и т.д.);

Множество можно задать перечислением всех его элементов в любом порядке. Если множество A, например, состоит из первых четырех букв русского алфавита, то записывают

• заданием общей характеристики (общих свойств) элементов данного множества (например, множество рациональных чисел, собаки, семейство кошачьих и т.д.);

Множество может быть задано с помощью характеристического свойства, т.е. такого свойства, которым обладают все элементы данного множества и не обладают никакие другие объекты. Если множество A задано с помощью характеристического свойства P, то записывают A = <x|p(x)>

Например, запись A = <x|x R,—7

N — множество натуральных чисел;

Z — множество целых чисел;

Q — множество рациональных чисел;

R — множество действительных чисел.

Пример 1.1. Запишем различными способами множество A, элементами которого являются натуральные числа, не превосходящие числа 6.

Решение. Натуральными числами, не превосходящими числа 6, являются: 1, 2, 3, 4, 5, 6. Поэтому множество A можно записать так: A = <1, 2, 3, 4, 5, 6>, или A = <1, 3, 5, 2, 4, 6>, или A = <6, 5, 4, 3, 2, 1>, или перечислением элементов в каком-либо другом порядке.

По условию множество A задано описанием характеристического свойства его элементов «Быть натуральным числом, не превосходящим числа 6». Используя это свойство, множество можно записать так: A = <x|x N,x б>.

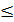
Пример 1.2. Прочитаем различными способами следующие записи:

а) 37 N ;

Решение. а) Число 37 является натуральным. Число 37 принадлежит множеству N. Число 37 — элемент множества N. Число 37 содержится во множестве N. Множество N содержит число 37.

б) Число 2,5 не является натуральным. Число 2,5 не принадлежит множеству N. Число 2,5 не является элементом множества N. Число 2,5 не содержится во множестве N. Множество N не содержит числа 2,5.

Пример 1.3. Используя понятие характеристического свойства, зададим следующие множества:

Решение. Множества A, B и C заданы способом перечисления элементов. Используя характеристические свойства, указанные множества можно задать следующим образом:

A — множество согласных букв русского алфавита;

B — множество цветов радуги;

C — множество дней недели.

Пример 1.4. Изобразим на числовой прямой элементы следующих множеств:

б) A = <x|x Z,—4 x

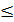
Источник