Ханойская башня способы решения
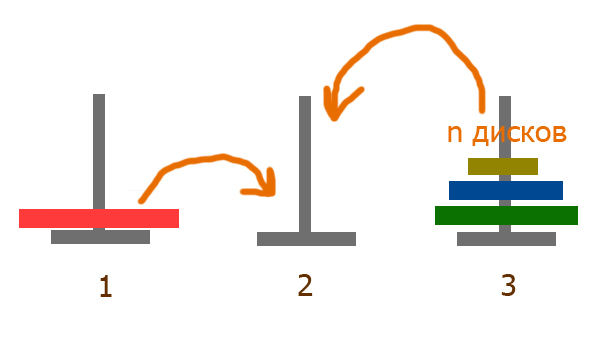
Есть три стержня A, B, и C. На стержень A надето N дисков, наверху самый маленький, каждый следующий диск больше предыдущего, а внизу самый большой. На другие стержни дисков не надето.
Hеобходимо перенести диски со стержня A на стержень C, пользуясь стержнем B, как вспомогательным, так, чтобы диски на стержне C располагались в том же порядке, в каком они располагаются на диске A перед перемещением.
При перемещении никогда нельзя класть больший диск на меньший.
Решение


Рекурсивный метод
Для того, чтобы переложить всю пирамиду, надо сначала переложить все, что выше самого большого диска, с первого на вспомогательный стержень, потом переложить это самое большой диск с первого на третий стержень, а потом переложить оставшуюся пирамиду со второго на третий стержень, пользуясь первым стержнем, как вспомогательным.
Всего получается 2 N-1 перекладываний.
Нерекурсивный метод
Стержню, на котором диски находятся в начале, дадим номер 0; стержню, на который их надо перенести — номер 2; и, соответственно, оставшемуся стержню — номер 1.
Пусть всего дисков N. Занумеруем диски в порядке увеличения радиуса числами 0,1,2. N-1.
Как известно, задача решается за 2 N-1 ходов. Занумеруем ходы числами 1,2. 2 N-1 .
Любое натуральное число i единственным образом представимо в виде i=(2t+1)*2 k , где t и k — целые (т.е. как произведение нечетного числа на некоторую степень двойки). Так вот, на i-ом ходе переносится диск номер k со стержня номер ((-1) N-k *t mod 3) на стержень номер ((-1) N-k *(t+1) mod 3).
если пpедставить что стержни, на котоpые одеваются диски, pасположены в yглах pавностоpоннего тpеyгольника, то самый маленький диск каждым нечетным ходом движется по (или пpотив, это от пеpвоначального кол-ва дисков зависит) часовой стpелки.
Все четные ходы опpеделяются однозначно. Какой диск меньше — тот и перекладывать (иначе противоречит условию). Т.к. тpогать диск 0 нельзя и класть больший на меньший тоже нельзя.
Отметим две закономерности:
- Hа каждом нечетном ходy происходит перенос наименьшего диска.
- Hаименьший диск всегда переносится циклически: либо A-B-C-A-B-C-. (в слyчае четного количества дисков), либо A-C-B-A-C-B-. (в слyчае нечетного).
А посемy полyчаем алгоритм:
1. Определяем число дисков, откyда находим как бyдет перемещаться наименьший диск (данный шаг делается в начале, притом один раз).
2. Смотрим номер хода: если нечетный — переносим наименьший диск в направлении, определенном в п.1. если четный — то возможный ход один единственный — берем наименьший из двyх верхних дисков и переносим его.
Можно написать немного по другому:
Для N от 1 до 2 k-1 выполнять
1. В двоичном представлении N найти самый правый ненулевой разряд. Обозначим номер этого разряда t.
2. Обозначим номер стержня, на котором находится диск t через i. Переместить диск t со стержня i на стержень (i+(-1) t ) mod 3.
Источник
Задача ханойская башня
Сегодня разберём известную задачу Ханойская башня. Подобные задачи способствуют повышению уровня грамотности при написании программ, развивают алгоритмические способности и поднимают общий тонус для участия в экзаменах и олимпиадах по информатике.
Задача : Есть три стержня. На одном из которых нанизаны диски. Диски располагаются в виде пирамидки(ханойской башни): в самом низу лежит самый большой диск, затем идёт чуть поменьше диск, затем ещё меньше диск и т. д. Необходимо переместить диски с одного стержня на другой. Можно использовать все три стержня, но при условии: перекладывать можно только по одному диску за ход, складывать диски можно только меньший на больший.
Нам необходимо составить алгоритм для решения данного задания при любом количестве n. Для начала докажем, что задача вообще имеет решение при любом количестве n. Для этого будем использовать метод математической индукции.
В основе метода математической индукции лежит принцип математической индукции.
Он заключается в следующем: некоторое утверждение справедливо для всякого натурального n, если оно справедливо для n = 1 и из справедливости утверждения для какого-либо произвольного натурального n = k следует его справедливость для n = k+1.
То есть, доказательство по методу математической индукции проводится в три этапа:
- во-первых, проверятся справедливость утверждения для любого натурального числа n (обычно проверку делают для n = 1);
- во-вторых, предполагается справедливость утверждения при любом натуральном n=k;
- в-третьих, доказывается справедливость утверждения для числа n=k+1, отталкиваясь от предположения второго пункта.
Используем метод математической индукции:
- Наша задача точно решается для одного диска. Это очевидно. Просто берём и перемещаем диск с одного стержня на другой.
- Пусть мы умеем перекладывать n дисков. Докажем, что тогда и n+1 мы также можем переложить.
- Пускай нам надо переложить n+1 дисков на второй стержень. Т.к. мы умеем перекладывать n дисков, то мы эту стопку переложим на третий стержень. Затем, положив самый большой диск на второй стержень, мы воспользуемся тем, что умеем перекладывать стопку из n элементов и переложим эту стопку с третьего стержня на второй. Таким образом, мы доказали, что задача решается для любого числа дисков.
Ещё раз о методе математической индукции. Мы доказали, что для одного диска всё работает отлично. Также мы доказали, что если для n дисков задача решается, то для n+1 тоже будет решаться. Но если вместо n подставить нашу 1, то уже для 2 тоже будет выполняться. В свою очередь 2 «тянет» за собой 3 и т.д. Таким образом, у нас задача будет решаться для любого натурального числа.
Сами наши рассуждения по поводу метода математической индукции нам подсказывают, что здесь можно воспользоваться рекурсией
Программу напишем на C#, т.к. этот язык в большинстве случаев принимается на олимпиадах по информатике. n-Количество дисков, i-номер стержня-источника, p-номер стержня-приёмника, v-вспомогательный стержень. Переменные соответственно i,p,v должны принимать значения от 1 до 3. Переменная n>0. Защита от «дурака» в данной функции не реализована. Если понадобится — реализуете сами. Также, здесь приведена сама функция Hanoy, которая и реализует всю работу. Остальные строки кода консольного приложения C# здесь опущены.
Как мы с вами разобрались, когда размышляли о математической индукции, чтобы переложить n дисков на стержень-приёмник, нам необходимо сначала переложить n-1 дисков на вспомогательный стержень, затем переложить самое большое кольцо на стрежень-приёмник, и повторить действия для n-1 дисков, переместив их из вспомогательного стержня, уже на стержень назначения. Таким образом, наша Ханойская башня из n элементов переместится со стержня источника на стержень-приёмник. Обратите внимание, что функция Hanoy вызывает сама себя, т.е. функцию Hanoy (Это и есть рекурсия!). Это происходит из-за того, что для перемещения Ханойской башни из n элементов, ей необходимо воспользоваться результатом своей же работы для n-1 элементов.
Запускаем нашу функцию Hanoy из функции Main (Для языка C# в консольном приложении) для 3х дисков:
Время работы пропорционально 2 n − 1, где n-количество дисков.
На сегодня всё. Надеюсь, Вам понравилась задача Ханойская башня. Давайте изучать классику Информатики вместе! Если у Вас что-то не получилось, пишите в комментариях. До новых встреч!
Источник
Сортировка «Ханойская башня»
Ханойские башни
Про знаменитую игру Эдуарда Люка́ на Хабре не писа́л только ленивый. Кажется, все покровы сорваны и что-то ещё по поводу алгоритма добавить уже невозможно. Но нет, у данной темы есть ещё скрытые ресурсы. Сегодня, в частности, мы переделаем алгоритм решения этой головоломки в полноценную сортировку. (Зачем? Just for fun. В пятницу можно.)
Данный пост посвящается памяти истинного гуру программирования Андрея Mrrl Астрелина, который когда-то мне просто и доходчиво объяснил этот алгоритм. Псевдокод ниже по тексту — его авторства.

В классической головоломке изначально диски на первом шесте уже упорядочены. Но мы разрешим им быть нанизанными в любом порядке.
Кроме того, размеры дисков предполагаются уникальными. Не будем цепляться за это ограничение и разрешим повторы.
Если позволить себе только эти две вольности, то начальные условия головоломки можно интерпретировать как массив (диски — это числа), а задача сводится к тому, что данный массив требуется отсортировать.
Остальные условия мы (почти) не меняем:
- У нас два вспомогательных шеста (пара пустых массивов).
- Можем переносить диски по одному.
- Класть только меньшие на бо́льшие (раз мы разрешили одинаковые размеры дисков, то также можно класть перемещаемый диск сверху на другие такого же размера).
- Имеем право сравнивать переносимый диск только с самым верхними дисками (то бишь, все 3 массива являются стеками).
Наша задача: взять классический рекурсивный алгоритм головоломки…
… и превратить его в сортировку!
На самом деле, от того что мы разрешили начальную неупорядоченность и повторы для размеров дисков — от этого принципиально не поменялось ничего. По большому счёту задача решаема всё тем же классическим рекурсивным способом. Самое главное что нужно понять — все перемещения дисков разделяются на несколько этапов, каждый из которых — это классичекий «ханой» в миниатюре.
То есть мы на каждом этапе рассматриваем не все имеющиеся диски, а только совокупность тех из них, которые удовлетворяют старым условиям. Отсортировав по классике это небольшое множество мы приблизим общее состояние системы к классической головоломке. Тогда мы опять берём то множество дисков, которое соответствует классике и применяем известный алгоритм вновь. И это множество будет бо́льшим, чем на предыдущем шаге! И так повторяем до тех пор, пока все диски на всех шестах вдруг не станут отличаться от классического состояния.
Нарушенная изначально система (тем, что на входе диски не упорядочены) самовосстанавливается с каждой итерацией.
Что касается разрешения повторов, то это вообще не имеет никакого значения. Потому что подряд идущие одинаковые диски мы просто перемещаем как один диск.
Алгоритм
Назовем столбики A, B, C (A в начале непустой).
А->С() — переложить один диск с А на С.
top(A), top(С) — размер верхнего диска А или С. Если столбик пуст, то этот размер = MaxInt.
В->С(К) — переложить с В на С все диски, размер которых меньше К (мы это можем сделать, если верхние диски А и С не меньше К).
swap() — переставить столбики В и С (или переименовать их — нам ведь все равно, где окажутся диски).
while(A) — цикл пока А не пуст.
Тогда работает такой алгоритм:
Сложность
В худшем случае сортировка стремится к сложности по времени для классического алгоритма, который хоть прост и изящен, но при этом максимально неэффективен. Насчёт лучшей и средней предположить затрудняюсь.
Насчёт памяти можно сказать, что если используется рекурсия, то и затраты будут соответствующие.
Реализация
Свой вариант на Python пока не написал (сделаю это позже). Однако ниже в разделе «Ссылки» накидал несколько ссылок, по которым можно посмотреть имплементации на различных языках. Особенно интересен вариант на Джаве. Автор не стал брать за основу общеизвестный рекурсивный способ для решения головоломки, а построил кратчайшее дерево путей. Предположительно, это является самым эффективным решением, если писать сортировку в стиле «Ханойской башни».
Характеристики алгоритма
| Название | Сортировка «Ханойская башня», Tower of Hanoi sort | |
|---|---|---|
| Автор идеи | Эдуард Люка́ | |
| Класс | Сортировки вставками | |
| Сравнения | Есть | |
| Временна́я сложность | лучшая | ? |
| средняя | ? | |
| худшая | O(2 n ) | |
Ссылки

Статьи серии:
- Excel-приложение AlgoLab.xlsm
- Сортировки обменами
- Сортировки вставками
- Сортировка библиотекаря
- Пасьянсная сортировка
- Сортировка «Ханойская башня»
- Сортировка выворачиванием
- Сортировка таблицей Юнга
- Сортировки выбором
- Сортировки слиянием
- Сортировки распределением
- Гибридные сортировки
В приложении AlgoLab данная сортировка теперь доступна. Хотя она относится к классу сортировок вставками, по причине экстравагантности алгоритма она помещена в раздел «Прочие сортировки». Ещё там есть ограничение — числа в сортируемом массиве могут быть только от 1 до 5 (связано с непростой прорисовкой дисков). Другие числа всё равно будут заменены на эти.
Также есть ограничение на размер массива — не более 20-ти элементов. Сделано это сугубо в Ваших же интересах — если возьмёте слишком большой массив, то, может так статься, что сортировать его придётся до глубокой старости.

Статья написана при поддержке компании EDISON Software, которая профессионально разрабатывает умное городское освещение и поддерживает сайты на питоне
Источник