Группы пространственных точек можно создавать следующими способами

5.4. ОПРЕДЕЛЕНИЕ И ПРИМЕРЫ ПРОСТРАНСТВЕННЫХ ГРУПП

Пространственной группой симметрии называется совокупность симметрических операций, присущих той или иной идеальной кри-

принципе пространственную гр

шире—ак к группу

симметрии всякой фигуры,еп —

трех измерениях. Однако кристаллические структу-

ры, по-видимому, единственныйти

п природных объектов,

рия которых описывается такими группами.

Поскольку для кристалла характерно решетчатое расположение

пространственная группа содержитв

группы трехмерную группу трансляций, относящуюся к одному из

типов Бравэ. Наряду с этим в нее,вообще говоря, входят и другие закрытые и открытые операции симметрии.

Значительную часть пространственных групп можно получить следующим способом. Пусть симметрия позициидл я некоторой точкиО пространства описывается кристаллографической точечной группой 5; иными словами, в точке О пересекаются элементы симметрии, входящие в группу 5. Эта группа относится к определен-

ной сингонии. Совместимс точкойО начало координат решетки,со — ответствующей данной сингонии, и размножим точку О, а вместе с

нейи элементы симметрии, черезне е проходящие,с помощью группы трансляций. Учтем также те результаты, к которым приводит сочетание элементов симметрии с трансляциями (раздел 5.2). В итоге получится геометрический образ одной из пространственных

Фактически такая процедура уже была в ряде случаев проделана. Так,размножаяос 3и 4, 6, перпендикулярными трансляциями, мы получили расположения, показанные на рис. 5.2.3, б, в, г.

Если подразумевать наличие трехмерной решетки, то эти рисунки

изображают проекции трех пространственных групп, обозначаемых

РЗ, и 4 Р&. Сходные группыс инверсионными осями изображе-

нын а рис. 5.2.5. Особенность пространственных групп, представ-

Источник

Пространственная группа

Под кристаллографической (пространственной) группой кристалла понимают набор всех операций симметрии, присущих рассматриваемой кристаллической решётке. Кристаллографическая группа представляет собой более широкое понятие, чем структурный тип, так как последний включает в себя, помимо характерных для решётки операций симметрии, распределение конкретных атомов по позициям симметрии внутри элементарной ячейки. Поэтому одной группе может соответствовать несколько структурных типов.

Содержание

Теорема Бибербаха

Две кристаллографические группы считаются эквивалентными, если они сопряжены в группе аффинных преобразований евклидова пространства.

С точностью до эквивалентности имеется 17 плоских и 219 пространственных кристаллографических групп; если же рассматривать пространственные группы с точностью до сопряжённости при помощи аффинных преобразований, сохраняющих ориентацию, то их будет 230. В размерности 4 существует 4895 кристаллографических групп с сохранением ориентации, или 4783 без сохранения ориентации [1] . Число кристаллографических групп n -мерного пространства с сохранением ориентации или без даётся последовательностями A004029 и A006227.

1. Всякая n -мерная кристаллографическая группа Γ содержит n линейно независимых параллельных переносов; группа G линейных частей преобразований (то есть образ Γ в GL_n ) конечна.
2. Две кристаллографические группы эквивалентны тогда и только тогда, когда они изоморфны как абстрактные группы.
3. При любом n имеется лишь конечное число n -мерных кристаллографических групп, рассматриваемых с точностью до эквивалентности (что является решением 18-й проблемы Гильберта).

Теорема позволяет дать следующее описание строения кристаллографических групп как абстрактных групп: Пусть L — совокупность всех параллельных переносов, принадлежащих кристаллографической группе Γ . Тогда L — нормальная подгруппа конечного индекса, изоморфная 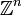и совпадающая со своим централизатором в Γ . Наличие такой нормальной подгруппы в абстрактной группе Γ является и достаточным условием того, чтобы группа Γ была изоморфна кристаллографической группе.

Группа G линейных частей кристаллографической группы Γ сохраняет решётку L ; иными словами, в базисе решетки L преобразования из G записываются целочисленными матрицами.

Возможные симметрии

В 3-мерных кристаллографических группах всегда присутствуют параллельные переносы, могут присутствовать повороты вокруг осей симметрии на углы 180° (ось симметрии 2-го порядка), 120° (3-го порядка), 90° (4-го порядка), 60° (6-го порядка), отражения относительно плоскости симметрии, отражения относительно центра симметрии (центра инверсии), а также сложные операции симметрии, а именно повороты вокруг осей с одновременным переносом на некоторый вектор в направлении этой оси (так называемая винтовая ось) и отражение относительно плоскости с одновременным сдвигом на некоторый вектор, параллельный этой плоскости (так называемая плоскость скользящего отражения).

Обозначения

Нумерация

Кристаллографические (пространственные) группы со всеми присущими им элеменатами симметрии сведены в международном справочнике «Международные кристаллографические таблицы» (англ. International Tables for Crystallography ), выпускаемых Международным союзом кристаллографии. Принято использование нумерации, приведённой в данном справочнике. Группы нумеруются с 1 по 230 в порядке увеличения симметрии.

Символика Германа — Могена

Символ пространственной группы содержит символ решётки Браве (заглавную букву P, A, B, C, I, R или F) и международный символ точечной группы. Символ решётки Браве обозначает наличие дополнительных узлов трансляции внутри элементарной ячейки: P (primitive) — примитивная ячейка; A, B, C (A-centered, B-centered, C-centered) — дополнительный узел в центре грани A, B или C соответственно; I (I-centered) — объёмноцентрированная (дополнительный узел в центре ячейки), R (R-centered) — дважды объёмноцентрированная (два дополнительных узла на большой диагонали элементарной ячейки), F (F-centered) — гранецентрированная (дополнительные узлы в центрах всех граней).

Международный символ точечной группы в общем случае формируется из трёх символов, обозначающих элементы симметрии, отвечающие трём основным направлениям в кристаллической ячейке. Под элементом симметрии, отвечающим направлению, понимается либо ось симметрии, проходящая по этому направлению, либо перпендикулярная ему плоскость симметрии, либо и то, и другое (в этом случае они записываются через дробь, например, 2/c — ось симметрии 2-го порядка и перпендикулярная ей плоскость скользящего отражения со сдвигом в направлении c). Под основными направлениями понимают:

• направления базисных векторов ячейки в случае триклинной, моноклинной и ромбической сингонии;
• направление оси 4-го порядка, направление одного из базисных векторов в основании элементарной ячейки и направление по диагонали основания ячейки в случае тетрагональной сингонии;
• направление оси 3-го порядка или 6-го порядка, направление одного из базисных векторов в основании элементарной ячейки и направление вектора по диагонали элементарной ячейки под углом 60° к предыдущему в случае гексагональной сингонии (сюда же включается тригональная сингония, которая в этом случае приводится к гексагональной ориентации элементарной ячейки);
• направление одного из базисных векторов, направление по пространственной диагонали элементарной ячейки и направление по биссектрисе угла между базисными векторами.

Символы Германа-Могена обычно сокращают, удаляя обозначения отсутствующих элементов симметрии по отдельным направлениям, когда это не создаёт неоднозначности, например, записывают P4 вместо P411. Также при отсутствии неоднозначности опускают обозначения осей второго порядка, которым перпендикулярны плоскости симметрии, например, заменяют 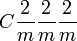на Cmmm .

Символ Шёнфлиса

Символ Шёнфлиса задаёт класс симметрии (основной символ и нижний индекс) и условный номер группы в пределах этого класса (верхний индекс).

• С_n, циклические группы — группы с единственным особым направлением, представленным поворотной осью симметрии, — обозначаются буквой С, с нижним цифровым индексом n, соответствующим порядку этой оси.

• С_ni — группы с единственной инверсионной осью симметрии сопровождаются нижним индексом i.

• C_v (от нем. vertical — вертикальный) — также имеет плоскость симметрии, расположенную вдоль единственной или главной оси симметрии, которая всегда мыслится вертикальной.

• C_h (от нем. horisontal — горизонтальный) — также имеет плоскость симметрии, перпендикулярную к главной оси симметрии.

• S (от нем. spiegel — зеркало) — для плоскости неопределенной ориентации, то есть не фиксированной ввиду отсутствия в группе иных элементов симметрии

• O, T — группы симметрии с несколькими осями высшего порядка — группы кубической сингонии — обозначаются буквой О в случае, если они содержат полный набор осей симметрии, или буквой Т — если в группе отсутствуют диагональные оси симметрии.

• D_n — является группой С_n с добавочной осью симметрии второго порядка, перпендикулярной исходной оси.

• D_nh также имеет имеет горизонтальную плоскость симметрии.
• D_nv также имеет имеет вертикальную плоскость симметрии.

n может равняться 1, 2, 3, 4, 6.

История

Происхождение теории кристаллографических групп связано с изучением симметрии орнаментов ( n = 2 ) и кристаллических структур ( n = 3 ). Классификация всех плоских (двумерных) и пространственных (трёхмерных) кристаллографических групп была получена независимо Фёдоровым (1885), Шёнфлисом (нем) (1891) и Барлоу (1894). Основные результаты для многомерных кристаллографических групп были получены Бибербахом (нем) [2] .

Источник

Классы пространственных объектов. Основные понятия

Классы пространственных объектов – однородные совокупности однотипных объектов, каждый из которых имеет одинаковое пространственное представление, в виде точек, линий, или полигонов, и общего набора атрибутивных полей, например, линейный класс пространственных данных для представления осевых линий дорог. Четыре основных типа классов пространственных данных – это точки, линии, полигоны и аннотации (названия для подписей на картах).

На рисунке ниже они представлены четырьмя наборами данных, относящимися к одной области: (1) — местоположения крышек люков в виде точек, (2) — линейные канализационные трубы, (3) — полигональные земельные участки и (4) — аннотации названий улиц.

На этой схеме, вы, возможно, также отметили потенциальное требование моделировать некоторые расширенные свойства объектов. Например, линии канализационных труб и местоположения люков составляют сеть коллектора ливневой канализации, т.е. систему, с помощью которой можно моделировать объём стока и потоки. Также следует отметить, как соседние участки используют общие границы. Большинство пользователей стараются поддерживать целостность общих границ объектов в этих наборах данных, используя топологию .

Как упомянуто выше, часто пользователи имеют потребность моделировать такие пространственные отношения и поведения в своих географических наборах данных. В этих случаях, можно расширить основную функциональность классов пространственных данных, добавляя ряд продвинутых элементов базы геоданных, таких как топология, наборы сетевых данных, наборы данных terrain и локаторы адресов.

Вы можете узнать больше о применении усовершенствованного поведения в базах геоданных в разделе Расширение классов пространственных объектов.

Типы классов пространственных объектов

Векторные объекты (географические объекты с векторной геометрией) разносторонние и являются часто используемыми географическими типами данных, хорошо подходящими для представления объектов с дискретными границами, например улицы, административные границы и земельные участки. Пространственный объект – это объект, который хранит свое географическое представление, представленное обычно в виде точки, линии или полигона, в качестве одного из свойств (полей) в строке. В ArcGIS классы пространственных данных – однотипные совокупности объектов с общим пространственным представлением и набором атрибутов, хранящиеся в таблице базы данных, например, класс линейных объектов, представляющий осевые линии дорог.

Создавая класс пространственных объектов, необходимо задать типа объектов для определения типа класса пространственных объектов (точка, линия, полигон и т.д.).

Как правило, классы пространственных объектов являются тематическими наборами точек, линий или полигонов, но в действительности существует семь типов классов пространственных объектов. Первые три поддерживаются в базах данных и базах геоданных. Остальные четыре поддерживаются только в базах геоданных.

• Точки: пространственные объекты, которые слишком малы, чтобы обозначать их линиями или полигонами, а также точечные местоположения (точки GPS).
• Линии:отображают форму и местоположение географических объектов, слишком узких для отображения в виде полигонов (центральные линии улиц, ручьи). Линии также используются для представления объектов, имеющих длину и не имеющих площади, таких как изолинии и границы.
• Полигоны: набор многосторонних площадных объектов, представляющих форму и местоположение однородных типов пространственных объектов, таких как административные районы, округа, участки земли, типы почвы и зоны землепользования.
• Аннотации: подпись на карте, содержащая параметры отображения текста. Например, помимо текстовой строки каждой аннотации, там хранятся и другие свойства – например точки фигуры для размещения текста, его шрифт и точечный размер, а также другие свойства отображения. Аннотация может также быть связанной с надписываемыми объектами и может содержать подклассы.

Геометрия и координаты пространственных объектов

Классы пространственных объектов содержат как геометрические формы каждого объекта так и их описательные атрибуты. Геометрию каждого объекта определяет, прежде всего, тип объекта (точка, линия, или полигон). Однако также могут быть определены и дополнительные геометрические свойства. Например, классы объекты могут быть одночастные и составные, могут иметь 3D вершины, линейные меры измерения (m-значения), а также могут содержать параметрически заданные кривые. Этот раздел даёт краткий обзор этих возможностей.

Одночастные и составные линии и полигоны

Линейные и полигональные классы пространственных объектов могут состоять из одной или нескольких частей. Например, одна административная единица может состоять из многих частей (Гавайские острова), но при этом являться одним пространственным объектом – штатом Гавайи.

Вершины, сегменты, высоты и измерения

Геометрия объектов составлена, прежде всего, из координатных вершин. Сегменты в линиях и полигонах охватывают вершины. Сегменты могут быть представлены прямыми линиями или параметрически заданными кривыми. Вершины в объектах могут также включать z-значения для представления высотных отметок и m-значения для представления измерений вдоль линейных объектов.

Типы сегментов линейных и полигональных объектов

Линии и полигоны задаются двумя ключевыми элементами: упорядоченным списком вершин, которые определяют форму линии или полигона и типами сегментов линии, используемых между каждой парой вершин. Каждая линия и полигон могут восприниматься как упорядоченный набор вершин, которые могут соединяться для формирования геометрической фигуры. Другой способ изображения каждой линии и полигона – упорядоченная последовательность соединенных сегментов, где каждый сегмент имеет тип: прямая линия, окружная дуга, эллиптическая дуга, или кривая Безье.

Тип сегмента по умолчанию – прямая линия между двумя вершинами. Однако, когда вам нужно определить кривые или параметрические фигуры, вы имеете в своём распоряжении три дополнительных типа сегментов: дуги окружностей, эллиптические дуги, и кривые Безье, которые могут быть определены. Эти фигуры часто используются для представления искусственных объектов, как например границы земельных участков или линии шоссе.

Вертикальные измерения с использованием z-значений

Координаты объектов могут включать X, Y или X, Y и Z вершины. Z-значения обычно используются для представления высот, но они могут представлять и другие измерения, такие как например годовое количество осадков или мера загрязнения воздушной среды.

Объекты могут иметь x,y координаты и, выборочно, добавленные значения z-высот.

Линейные измерения с использованием m-значений

Вершины линейных объектов могут также содержать m-значения. Некоторые ГИС приложения используют систему линейных измерений для интерполяции расстояний вдоль линейных объектов, таких как дороги, потоки (рек, ручьёв) и трубопроводы. Вы можете присвоить m-значение каждой вершине объекта. Обычно используемый пример – система измерения километровых столбов на шоссе, используемая отделами перевозки для регистрации состояний дорожного покрытия, пределов скорости, местоположений несчастных случаев, и других инцидентов вдоль шоссе. Наиболее используемые меры измерения — расстояние на километровом столбе от установленного положения, например линия округа, и расстояние от опорного маркера.

Вершины для измерений могут иметь вид x,y,m или x,y,z,m.

Поддержка таких типов данных часто называется системой линейных координат . Обработку нахождения координат событий в этих системах измерений также называют динамической сегментацией .

Координаты линейных измерений формируют блоки для построения этих систем. В реализации линейной привязки в ArcGIS, термин маршрут обозначает любой линейный объект, например улицу города, шоссе, реку или трубу, имеющие уникальный идентификатор и общую систему измерения вдоль каждого линейного объекта. Совокупность маршрутов с общей системой измерения может быть построена на основе линейного класса пространственных объектов как показано ниже:

Для получения дополнительной информации см. Обзор системы линейных координат.

Допуски объектов

Точность местоположений и поддержка рабочей среды управления данных с высоким разрешением очень важны при управлении ГИС данными. Основное требование – это возможность хранить информацию о координатах с достаточной точностью. Точность координат характеризует количество десятичных знаков, используемых для записи информации о местоположении. Это определяет разрешение, при котором собираются и управляются пространственные данные.

Так как базы геоданных и базы данных могут записывать координаты с высокой точностью, пользователи могут создавать наборы данных с высоким уровнем точности, и с большим разрешением, поскольку инструменты захвата данных и сенсоры постоянно совершенствуются (ввод геодезических и инженерных данных, захват данных COGO, повышенное разрешение изображений, данные лидара, чертежи строений из САПР и т.д.).

ArcGIS записывает координаты как целые числа и может хранить местоположения с очень высокой точностью. В различных операциях ArcGIS, координаты объекта обрабатываются и управляются с использованием некоторых ключевых геометрических свойств. Эти свойства определяются при создании каждого класса пространственных объектов или набора классов объектов.

Следующие геометрические свойства помогают определить координатное разрешение и обрабатываемый допуск, используемые в различных процессах пространственной обработки и геометрических операциях.

• Разрешение по x,y: точность, с которой записываются координаты пространственных объектов
• Допуск x,y: кластерный допуск, используемый для пространственных объектов с совпадающей геометрией. Используется в топологии, при наложении пространственных объектов и прочих подобных операциях
• Допуск z и разрешение z: свойства допуска и разрешения для вертикальных измерений координат в трехмерных наборах данных (например, в измерениях высот)
• Допуск m и разрешение m: свойства допуска и разрешения для измерений вдоль линейных пространственных объектов, используется с наборах данных с системами линейных координат (например, расстояния вдоль дорог в метрах).

Разрешение x,y

X,y разрешение класса пространственных данных или набора классов пространственных данных — числовая точность представления данных, используемая для хранения значений x,y координат. Точность очень важна для аккуратного представления пространственных объектов, анализа и картирования.

X,y разрешение определяет число десятичных знаков или значащих разрядов, используемых для хранения координат объектов (и x, и y). Разрешение можно сравнить с очень мелкой ячейкой сетки, к которой привязаны все координаты. Значения координат хранятся и обрабатываются в ArcGIS как целые числа. Соответственно, иногда эта сетка грида называется целочисленной сеткой или координатной сеткой

Разрешение определяет расстояние между ячейками в координатной сетке, которой соответствуют все координаты. X,y разрешение выражается в единицах данных (зависят от координатной системы), например в футах, метрах UTM, или метрах проекции Альберса.

По умолчанию разрешение x,y в классах объектов составляет 0.0001 м или эквивалент этого значения в единицах системы координат набора данных. Например, если класс пространственных объектов использует футы (проекция State Plane), значение по умолчанию составит 0.0003281 фута (0.003937 дюйма). Если координаты даны в градусах широты-долготы, разрешение x,y будет 0,000000001 градуса.

На рисунке ниже показан общий вид координатной сетки, где все значения координат замыкаются на эту сетку грида. Решетка покрывает экстент каждого набора данных. Мелкий размер этих ячеек (расстояние между линиями сетки) определяется x,y разрешением, которое достаточно мало.

Если необходимо, вы можете заменить значение x,y разрешения по умолчанию и установить другое для каждого класса пространственных объектов или набора классов объектов. Установка меньшего значения x,y разрешения может потенциально увеличить объём хранимых данных и время обработки наборов данных, по сравнению с большими значениями x,y разрешения.

X, Y допуск

Когда вы создаете класс пространственных объектов, необходимо задать допуск x,y. Допуск x,y используется, чтобы установить минимальное расстояние между координатами при таких операциях кластеризации, как проверка топологии, создание буферных зон или наложение полигонов, а также при некоторых операциях редактирования.

Х,y допуск влияет на операции обработки объекта, так как определяет минимальное расстояние, разделяющее все координаты объекта (узлы и вершины) в течение тех действий. В процессе данного определения, также определяется расстояние, на которое координата может перемещаться по оси x или y (или по обеим осям) в течение операций кластеризации.

X,y допуск — чрезвычайно маленькое расстояние (типовое значение составляет 0,001 метра в единицах земли). Он используется для исправления неточностей пересечения положения координат в ходе кластерных операций. При обработке классов пространственных объектов с помощью геометрических операций, те координаты, расстояние по х и у между которыми оказываются в пределах этого допуска x,y, считаются совпадающими (т.е. с одинаковым местоположением x,y). Таким образом, сгруппированные координаты перемещаются в общее место.

Обычно, менее точная координата перемещается к расположению более точной координаты, или новое положение считается как взвешенное среднее расстояние между координатами в кластере. В этих случаях средневзвешенное расстояние основывается на рангах точности кластеризованных координат.

Более подробная информация о задании рангов точности для классов объектов находится в разделе Топология в ArcGIS.

Процесс кластеризации работает путем перемещения по карте и идентификации кластеров координат, попадающих в пределы допуска x,y друг от друга. ArcGIS использует этот алгоритм для обнаружения, приведения в порядок, и управления общей геометрией объектов. Это означает, что координаты считаются совпадающими (и замыкаются к общему местоположению координат). Это основа многих принципов работы и операций ГИС. Примеры находятся в разделе Обзор топологии в ArcGIS.

Максимальное расстояние, на которое координата может переместиться в новое положение в ходе таких операций — квадратный корень, умноженный на двойной x,y допуск. Кластерный алгоритм итеративен, таким образом, в некоторых случаях, возможно, что положения координат сместятся более, чем на это расстояние.

X,y допуск по умолчанию равен 0,001 метрам или эквивалентному расстоянию в единицах измерения реального мира набора данных (т.е., 0,001 метра на земле). Например, если у вас система координат в футах, допуск x,y по умолчанию будет 0,003281 фута (0,03937 дюйма).

Значение по умолчанию для x,y допуска – стандартное x,y разрешение, увеличенное в 10 раз, и это значение рекомендуется использовать в большинстве случаев. У вас есть опция установить для менее точных данных большее значение допуска, или для высокоточных данных — меньшее.

Важно отметить, что X,Y допуск не предназначен для генерализации геометрических форм. Взамен этому, он предназначен для объединения работы линии и границ в течение топологических операций. Это означает объединение координат, которые попадают в пределы очень маленьких расстояний друг от друга. Поскольку координаты могут передвигаться как по оси x, так и по оси y, равно как и x,y допуск, много потенциальных проблем могут быть решены обработкой наборов данных командами, использующими x,y допуск. Сюда относится перемещение при очень небольших несовпадениях, автоматическое удаление двойных сегментов и уточнение координат вдоль линий границ.

Ниже приведены некоторые полезные замечания:

• В целом, вы можете использовать x,y допуск, равный x,y разрешению, увеличенному в 10 раз, и ожидать хороших результатов.
• Чтобы координаты далеко не перемещались, поставьте маленький допуск x,y. Однако, слишком маленький x,y допуск (равный утроенному значению x,y разрешения), может должным образом не объединить работу линии совпадающих границ и координат.
• И наоборот, если допуск слишком велик, координаты пространственных объектов могут «схлопнуться». Это может повлиять на точность отображения границ пространственных объектов.
• Значение вашего x,y допуска не должно приближаться к значению разрешения ваших данных на карте. Например, на карте масштаба 1:12 000, один дюйм равен 1 000 футов, а 1/50 дюйма равняется 20 футам. Вы можете сохранить передвижение координат, используя X,Y допуск, ниже данных значений. Помните, что стандартное значение x,y допуска в данном случае составит 0,0003281 футов, что будет являться весьма подходящим значением по умолчанию для x,y допуска: фактически, лучше использовать значения x,y допуска по умолчанию во всех случаях, не считая исключительных.
• В топологии вы можете установить разряд координат каждого класса пространственных объектов. Вам захочется установить координатный разряд ваших самых точных объектов (например, полученные при топосъёмке пространственные объекты) равному 1 и менее точных объектов равному 2, 3, и так далее, в нисходящей последовательности разрядов точности. Это приведёт к тому, что другие координаты объекта с высшим разрядом точности (и поэтому, с низшей координатной точностью), будут привязаны к более точным объектам с низшим разрядом.

Хранение класса объектов

Каждый класс пространственных объектов хранится в отдельной таблице. Столбец shape в каждой строке используется для хранения геометрии или формы каждого объекта.

В таблице класса пространственных объектов:

• Каждый класс пространственных данных является таблицей.
• Индивидуальные объекты представлены в виде записей.
• Атрибуты пространственных объектов записываются в столбцы.
• Столбец shape содержит геометрию каждого объекта (точка, линия, полигон и т.д.).
• Поле Object ID содержит уникальный идентификатор для каждого объекта.

При создании класса линейных объектов в базе геоданных в класс пространственных объектов автоматически добавляется дополнительное поле для записи значений длины линии. При создании класса полигональных объектов в базе геоданных в класс пространственных объектов автоматически добавляется два дополнительных поля для записи значений длины (периметра) и площади всех полигональных объектов. Единицы измерения для этих значений зависят от пространственной привязки, определенной для класса пространственных объектов. Имена этих полей варьируются в зависимости от базы данных и используемого пространственного типа. Эти поля являются обязательными и не могут быть изменены.

Расширение классов пространственных объектов

Каждый класс пространственных объектов — это собрание географических объектов с одинаковым типом геометрии (точка, линия или полигон), с однотипными атрибутами и одинаковой пространственной привязкой. Классы пространственных объектов, хранящиеся в базах геоданных могут быть расширены для решения необходимых задач. Здесь приведены некоторые примеры того, как можно расширить функциональность классов пространственных данных, используя базу геоданных.

Содержит совокупность пространственно связанных классов объектов, или используется для построения топологии, сетей, наборов кадастровых данных и наборов данных terrain.

Управлять набором атрибутивных подклассов пространственных объектов в одном классе пространственных объектов. Обычно применяется к таблицам классов пространственных объектов для управления поведением подтипов тех же типов объектов.

Установить список допустимых значений или диапазон допустимых значений для атрибутивных полей. Использовать домены для вспомогательного обеспечения целостности атрибутивных значений. Домены часто используются для классификации данных (класс дорог, коды зон, классификаторы использования земель).

Построить отношения между двумя таблицами с использованием общего ключа. Найти связанные записи во вторичной таблице, основываясь на записях, выбранных в основной таблице, и т.д.

Моделировать способ совместного использования геометрии. Например, соседние округа имеют общую границу. Также, полигоны округов располагаются внутри стран, которые их полностью содержат.

Моделировать транспортную связность и поток. Необходимо установить Дополнительный модуль ArcGIS Network Analyst для ArcGIS for Desktop .

Моделировать сети коммуникаций и трассировку.

Моделировать нерегулярные триангуляционные сети (TIN) и управлять большими коллекциями точек lidar и sonar. Необходимо установить Дополнительный модуль ArcGIS 3D Analyst для ArcGIS for Desktop .

Для интеграции и поддержания геодезической информации для подразделений и планов земельных участков как части непрерывного набора данных модели cadastral в базе геоданных. Также, для постепенного повышения точности набора данных участков при вводе новых планов и описаний.

Разместить события вдоль линейных объектов с измерениями.

Управлять многократно использующимися картографическими представлениями и продвинутыми картографическими правилами рисования.

Управлять рядом ключевых технологических процессов ГИС управления данными, например длинными транзакциями на обновление данных, историческими архивами и многопользовательским редактированием. Требуется использование баз геоданных ArcSDE.

Источник