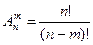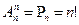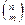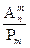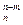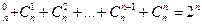Группа студентов изучает 7 учебных дисциплин сколькими способами

Сочетания

Конечные упорядоченные подмножества, содержащие по m элементов, выбранных из n элементов по m элементов основного множества, называются размещениями из n элементов по m элементов.

Размещения.

Пусть дано некоторое конечное множество А, состоящее из n различных элементов. Выберем некоторым образом из n элементов m различных элементов, и

будем составлять из этих m элементов различные упорядоченные множества.

Число всех возможных размещений из n элементов по m элементов обозначается 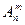_. Число размещений из n элементов по m можно записать в виде формулы:

Пример: Группа учащихся изучает 7 учебных дисциплин. Сколькими способами можно составить расписание занятий в понедельник, если в этот день недели должно быть 4 различных урока?

Решение. Число способов равно числу размещений из 7 элементов по 4, т.е. равно А 4 ₇ =7·6·5·4=840

Число размещений и число перестановок связаны формулой:

Конечные неупорядоченные множества, содержащие m различных элементов, выбранных из n элементов заданного множества, называются сочетаниями из n элементов по m элементов. Обозначается 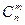или

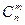
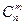
Число различных неупорядоченных множеств, содержащих по m различных элементов, выбранных из элементов, будет вычисляться по формуле: =

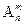
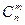
Используя формулы для подсчета числа перестановок Р_m и числа размещений , получим =

Пример:группу учащихся колледжа должна экзаменовать по математике комиссия, состоящих из 7 человек. Сколькими способами может быть составлена комиссия, если в колледже 14учителей математики?

Решение: используем формулу подсчета числа сочетаний = .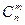

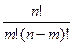
Здесь n=14, а m = 7, тогда = .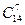

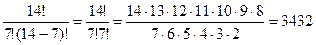
Для числа сочетаний справедливы равенства:

= С, С= + С, а также С

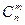
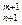
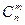
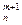
.Последнее свойство иногда формулируется в виде следующей теоремы о конечных множествах: Число всех подмножеств множества, состоящего из n элементов, равно 2 n .

Контрольные вопросы:

Дайте определение числовой последовательности.

Перечислите способы задания последовательностей.

Какие последовательности называют ограниченными?

Сформулируйте определение предела числовой последовательности.

Сформулируйте необходимые и достаточное условия сходимости последовательности.

Дайте определение предела функции в точке.

Перечислите основные теоремы о пределах функции в точке.

Сформулируйте определение числового ряда.

Какой ряд называется сходящимся, расходящимся?

Сформулируйте необходимое условие сходимости ряда.

Сформулируйте признак Даламбера сходимости рядов.

Какой ряд называют абсолютно сходящимся?

Какой ряд называют условно сходящимся?

Запишите формулу разложения функции в ряд Маклорена.

Понятие множества, элемента множества, подмножества.

Способы обозначения и задания множества.

Понятие равных множеств, пустого множества.

Пересечение множеств. Непересекающиеся множества.

Переместительный и сочетательный законы.

Сумма (объединение) множеств.

Разность множеств. Дополнение до множества.

Прямое произведение множеств.

Эквивалентные множества. Взаимно однозначное соответствие

Сформулируйте определение графа.

Перечислите способы задания графов.

Сформулируйте определение комбинаторики, как раздела математики.

Сформулируйте определение факториала.

Сформулируйте определение перестановок.

Дайте понятие размещения и сочетания.

Домашнее задание

Заполните в рабочей тетради занятие 7. 8, 9, 10

Лекция № 5

Тема: Основные понятия теории вероятности и математической статистики

План:

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Элементы комбинаторики контрольная работа
методическая разработка

Элементы комбинаторики контрольная работа

Скачать:

Вложение	Размер
elementy_kombinatoriki_kontrolnaya_rabota.docx	28.31 КБ

Предварительный просмотр:

АДМИНИСТРАТИВНАЯ КОНТРОЛЬНАЯ РАБОТА

по дисциплине «Математика»

Цель к/р : проверить соответствие знаний/понимания и умений студентов Государственным требованиям к уровню подготовки по теме «Элементы комбинаторики».

Контрольная работа состоит из 2 вариантов, каждый вариант включает 7 заданий. Работа рассчитана на 2 академических часа.

Студенты должны знать/понимать:

• Правила комбинаторики;
• Понятия комбинаторики: размещения, сочетания, перестановка и формулы для их вычисления;
• Классическое определение вероятности, свойства вероятности, теорему о сумме вероятностей;
• Числовые данные и их характеристики.

Студенты должны уметь решать:

• Комбинаторные задачи методом перебора и по правилу умножения;
• Задачи с размещениями, сочетаниями, перестановками;
• Практические задачи с использованием понятий и правил комбинаторики;
• Задачи на вычисление вероятностей событий.

Правильно выполнены все задания — «5»
Правильно выполнены пять и более заданий с недочетами — «4»

Правильно выполнены 4 и более задания с недочетами — «3»
Правильно выполнено менее 50% заданий — «2»

Приложение: образец заданий в 2 вариантах на 1 листе

Административная контрольная работа по теме: «Элементы комбинаторики».

1.Вычислить

1.Вычислить

2.Вычислить 6!-

2. Вычислить

3.Несколько стран в качестве символа своего государства решили использовать флаг в виде трех горизонтальных полос одинаковых по ширине, но разных по цвету: белый, синий, красный.

Сколько стран могут использовать такую символику при условии, что у каждой страны свой, отличный от других, флаг?

3. «10 выпускников пришли в кафе отпраздновать окончание школы, но не могли решить, как сесть, т.е. в каком порядке. На выручку пришёл официант, который предложил сесть сегодня, как придётся, а на другой день сесть по — другому и так до тех пор, пока не наступит такой день, когда они сядут как в первый раз. Тогда их официант обещал угостить бесплатным обедом. Как вы думаете, долго ли друзьям ждать бесплатного обеда?»

4.Сколько имеется слов длиной 3 с неповторяющимися буквами в алфавите из 6 букв?

4.Студенты 1 курса изучают 10 предметов. Сколькими способами можно составить расписание на один день, чтобы в нем было 4 различных предмета?

5.Сколько различных двухзначных чисел можно составить, используя цифры 1, 2, 3, 4 при условии, что ни одна цифра не повторяется?

5.Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что ни одна цифра не повторяется?

6.Имеется 5 цветков разного цвета. Обозначим их буквами a, b, c, d, e. Требуется составить букет из трех цветков.

6.В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?

7.Из шести врачей поликлиники двух необходимо отправить на курсы повышения квалификации. Сколькими способами это можно сделать?

7.В группе 7 студентов успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в олимпиаде по предмету?

Источник

Группа студентов изучает 10 учебных дисциплин?

Математика | 10 — 11 классы

Группа студентов изучает 10 учебных дисциплин.

Сколькими способами можно составить расписание занятий на понедельник, если в этот день недели должно быть 4 различных пары?

Первая пара — один из 10ти предметов, вторая пара — один из девяти пердметов, третья пара — один из восьми предметов, четвертая пара — одна из оставшихся семи пар итого : 10 * 9 * 8 * 7 = 5040 вариантов составления рассписания.

Надо составить похожую задачу и решить эту :Группа студентов изучает английский и французский?

Надо составить похожую задачу и решить эту :

Группа студентов изучает английский и французский.

Английский изучает 15 человек а французский 12.

Оба языка изучает 7 человек.

Сколько всего студентов в группе?

Студенту необходимо сдать 6 экзаменов за 6 дней?

Студенту необходимо сдать 6 экзаменов за 6 дней.

Сколькими способами можно составить ему расписание экзаменов?

Элементы комбинаторики : Вариант – I?

Элементы комбинаторики : Вариант – I.

№1. Сколько различных “слов”, состоящих из трех букв можно составить из букв слова “Атлет”?

А если слова содержат не менее трех букв?

№2. Группа школьников изучает 8 различных дисциплин.

Сколькими способами можно составить расписание занятий во вторник, если в этот день должно быть 5 различных занятий?

№3. В урне 15 белых и 13 черных шаров.

Сколькими способами можно выбрать 10 шаров, что бы среди них было : а) 10 черных ; б) 4 белых и 6 черных.

№4. Игральная кость бросается 3 раза.

Сколько существует вариантов выпадения очков в данном опыте?

Напишите некоторые из них.

Студенты 1 курса изучают 10 предметов?

Студенты 1 курса изучают 10 предметов.

Сколько способами можно составить расписание на один день чтобы в нем было 4 различных предмета?

Учащиеся 9 класса изучают 10 предметов сколькими способами можно составить расписание уроков на один день так чтобы было 6 различных уроков?

Учащиеся 9 класса изучают 10 предметов сколькими способами можно составить расписание уроков на один день так чтобы было 6 различных уроков.

В группе 18 предметов и 6 уроков в день ?

В группе 18 предметов и 6 уроков в день .

Несколькими способами можно составить расписание на один день ?

Студентам надо сдать 4 экзамена за 8 дней?

Студентам надо сдать 4 экзамена за 8 дней.

Сколькими способами можно составить расписание сдачи экзаменов, если в один день сдается только один экзамен?

Решить по правиле произведения.

В третьем классе в понедельник должно быть 4 урока : математика, русский язык, литературное чтение, технология?

В третьем классе в понедельник должно быть 4 урока : математика, русский язык, литературное чтение, технология.

Сколько различных вариантов расписания можно составить на этот день в 3 классе?

Группа студентов 1курса изучают 12предметов в пятницу 4урока причем все уроки разные сколькими способами можно составить расписание на пятницу?

Группа студентов 1курса изучают 12предметов в пятницу 4урока причем все уроки разные сколькими способами можно составить расписание на пятницу.

В классе 5 уроков , сколькими способами можно составить расписание на один день?

В классе 5 уроков , сколькими способами можно составить расписание на один день.

Вы открыли страницу вопроса Группа студентов изучает 10 учебных дисциплин?. Он относится к категории Математика. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Математика, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

80 30 820 40 1860 6390 600 900 1300 2000 5000278343000085000.

Источник